Abstract. For several years, a significant disagreement has persisted between (mainly) philosophers, and (mainly) physicists concerning the consequences of the empirical violation of Bell's inequality. On the one hand, it is claimed that empirical violations of Bell's inequality show us that the world is “non-local,” which might give rise to a serious conflict with the special theory of relativity. On the other hand, several authors maintain that this conflict can be avoided by giving up a “realistic” interpretation of quantum mechanics. I use a recent derivation of a Bell-type inequality from Reichenbach's principle of the common cause to explicate the different notions of “non-locality” and “realism” involved in the debate, and to assess the adequacy of the different claims. My two main conclusions are: First, if “realism” is understood as the existence of sufficient conditions for the measurement outcomes in the experimental setups under consideration, giving it up will not allow us to maintain locality. Second, however, I will argue that there is, in fact, a plausible notion of “realism” which we could reject in order to save locality. Instead of challenging the special theory of relativity, this option impugns common notions of causality.
1 From a Dilemma to a “Monolemma”
The empirical violation of Bell's inequality forces us to deny at least one of the premises from which it is derived.1 There is, however, a significant disagreement as to what assumptions about the physical world or our theories of it are at stake.
On the one hand, people (mainly physicists) maintain that it is an open question whether we should admit that there are non-local interactions in the world, and thus challenge the special theory of relativity,2 or whether we should, rather, give up a certain notion of realism:
The experimental violation of mathematical relations known as Bell's inequalities sounded the death knell of Einstein's idea of “local realism,” in quantum mechanics. But which concept, locality or realism, is the problem? Aspect 2007, 866
On the other hand, (mainly) philosophers urge that this stance is untenable because even if we dispense with our cherished notions of realism we have to accept non-local interactions in the world. Their argument is the following.
One can derive Bell's inequality from essentially the following two assumptions:
The outcome of a measurement at one wing in an Einstein-Podolsky-Rosen (EPR) experiment3 does not causally depend on the outcome or the measurement operations at the other wing.
The outcomes of the measurements in an EPR experiment are co-determined by some events which are themselves causally independent of the measurement operations.
The first of these two assumptions comprises locality conditions, for which one can make strong supportive arguments based on the theory of special relativity. The second assumption postulates something akin to what Einstein called, in the EPR paper, “elements of reality.” The existence or not of elements of reality, and the properties that they instantiate should be, moreover, independent from the actions of the observer, according to the second assumption.
Let us, in line with this “zeroth” characterization,
abbreviate the two set of assumptions by “
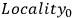 ” and “
” and “
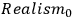 ,” respectively.
Then, the derivation of Bell's inequality can be represented as the
following entailment. Let us call it, for the purposes of the present discussion,
“Bell's theorem”:
,” respectively.
Then, the derivation of Bell's inequality can be represented as the
following entailment. Let us call it, for the purposes of the present discussion,
“Bell's theorem”:
(
 &
&
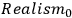 )
)
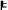 Bell's Inequality.
Bell's Inequality.
Because of the empirical violations of the consequence of this entailment, i. e., of Bell's inequality, at least one of the two sets of premises has to be false. If the derivation is minimal in the sense that dropping one of the premisses will lead to an invalid argument, then the argument gives no reason to give up more than one of the two problematic sets of premises.
However, according to several authors, the derivation from the above two premises is not minimal, because, according to them, Realism is a necessary condition for Locality, i. e.
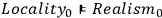 .
.
They take it that Einstein, Podolsky, and Rosen have established that claim:
Many believe that because Bell starts by assuming the world conforms to what is called local realism, he therefore proved that either locality or realism is violated. Thus, the world could be local if it violates “realism.” But this idea overlooks—or misunderstands—that the original “EPR” argument of Albert Einstein, Boris Podolsky and Nathan Rosen rules out the possibility of quantum locality without the realism Bell uses. Albert and Galchen 2009, 31
If Albert and Galchen are right and Realism is, indeed, a necessary condition for Locality, “Bell's theorem” gives rise to a derivation of Bell's inequality from the assumption of Locality alone:
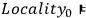 Bell's Inequality.
Bell's Inequality.
This is also the conclusion that Maudlin draws:
So experiments verifying the violation of Bell's inequality would doom locality tout court. Maudlin 2002, 20
Thus, according to Albert, Galchen, and Maudlin, we cannot avoid the challenges, which a violation of Locality most likely poses to the theory of special relativity, by giving-up Realism alone.
2 Details of the Derivation of Bell's Inequality
In order to assess the adequacy of the divergent claims by, on the one hand, the physicist Aspect and, on the other hand, Albert, Galchen, and Maudlin, I will sketch, in the following, a more detailed and explicit derivation of a Bell-type inequality, which is based on work by Graßhoff et.al. 2005. This derivation is minimal with respect to an important class of other derivations. For example, the authors do not require different correlations to have the same common cause. I will subdivide the derivation into two steps so as to be able to compare it more readily with Maudlin's, and Albert and Galchen's arguments to the effect that Bell's inequality derives from locality conditions alone.
I will set aside some auxiliary assumptions. This is, of course, always a pragmatic instead of a principled decision and depends on where one wants to put the focus of the investigation. Most of the auxiliary assumptions are made explicit by Graßhoff et.al. 2005, but even there the authors did, for instance, not address, in any detailed manner, the question as to how to interpret the probabilities which are used in the derivation. I will bracket out this question here, too.
The first step of the derivation proceeds from three principal assumptions to an intermediate conclusion. The assumptions involve perfect correlations, causal independence of correlated outcomes, and a variant of Reichenbach's 1956 principle of the common cause:
• PCORR: Upon parallel measurements, the outcomes in an EPR experiment are perfectly anti-correlated.
• C-OI: The measurement outcomes at one wing are not causally relevant for the outcomes at the other wing.
• SCR: If two types of events
 and
and
 are correlated and neither
are correlated and neither
 is causally relevant for
is causally relevant for
 nor vice-versa then there exists a third type
of event
nor vice-versa then there exists a third type
of event
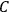 which statistically “screens-off”
which statistically “screens-off”
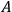 from
from
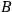 :
:

|
From these three assumptions follows (given the auxiliary assumptions
characterizing the experimental setup and a suitable interpretation of the
probabilities) that there are sufficient conditions for the correlated effects.4
More precisely, for instance, setting up both the apparatus on the left
and on the right to
measure the spin of the particle relative to direction no. 1,
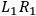 ,
together with a certain type of screening-off event,
,
together with a certain type of screening-off event,
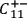 ,
is a sufficient condition for the outcome of the measurement at the left wing
being
,
is a sufficient condition for the outcome of the measurement at the left wing
being
 , and also for the outcome at the right wing being
, and also for the outcome at the right wing being
 .
In a similar way, we arrive at the following four conditional statements:
5
.
In a similar way, we arrive at the following four conditional statements:
5
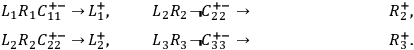
|
Since we assume that
• C-P:: the measurement operations on the particle at the distant wing of the experimental setup are not causally relevant to the outcome of measurements on the particle in question,
the above conditionals should be true even without the statements,
in the antecedent,
that the measurement apparatus at the distant wing is set up in a particular
way.
That is, for instance, we can discard
 from the sufficient condition
for
from the sufficient condition
for
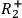 ,
or
,
or
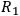 from the sufficient condition for
from the sufficient condition for
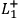 .
This manipulation of the
antecedent, is an application of the regularity theory of causality as
developed by
Mackie 1974, and elaborated by, e.g., Baumgartner 2008, and Graßhoff and May 2001.
According to these theories of causality, if, for instance,
.
This manipulation of the
antecedent, is an application of the regularity theory of causality as
developed by
Mackie 1974, and elaborated by, e.g., Baumgartner 2008, and Graßhoff and May 2001.
According to these theories of causality, if, for instance,
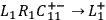
|
would cease to be valid when
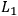 is discarded,
is discarded,
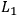 would, in fact, be causally relevant for
would, in fact, be causally relevant for
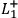 given certain additional conditions.6
given certain additional conditions.6
Although I here performed the transition from the conditionals which contain
both measurement settings to the conditionals which contain only one of them
using a theory of causal regularities,
the essential assumption involved in the transition is again screening-off.
For, under suitable interpretations of the probabilities,
the above manipulation of the conditionals is tantamount to
reading C-PI as the claim that, e.g.,
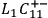 screens off
screens off
 from
from
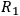 , i. e.,
, i. e.,
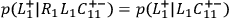
|
or, equivalently,
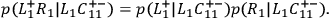
|
Thus, if we do not take the distant measurement operations to be causally relevant for the nearby outcome and assume an interpretation of causal irrelevance which either implicitly or explicitly is a screening-off condition, we end up with the following sufficient conditions for the outcomes:
• SUFF::
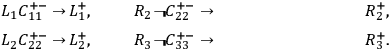
|
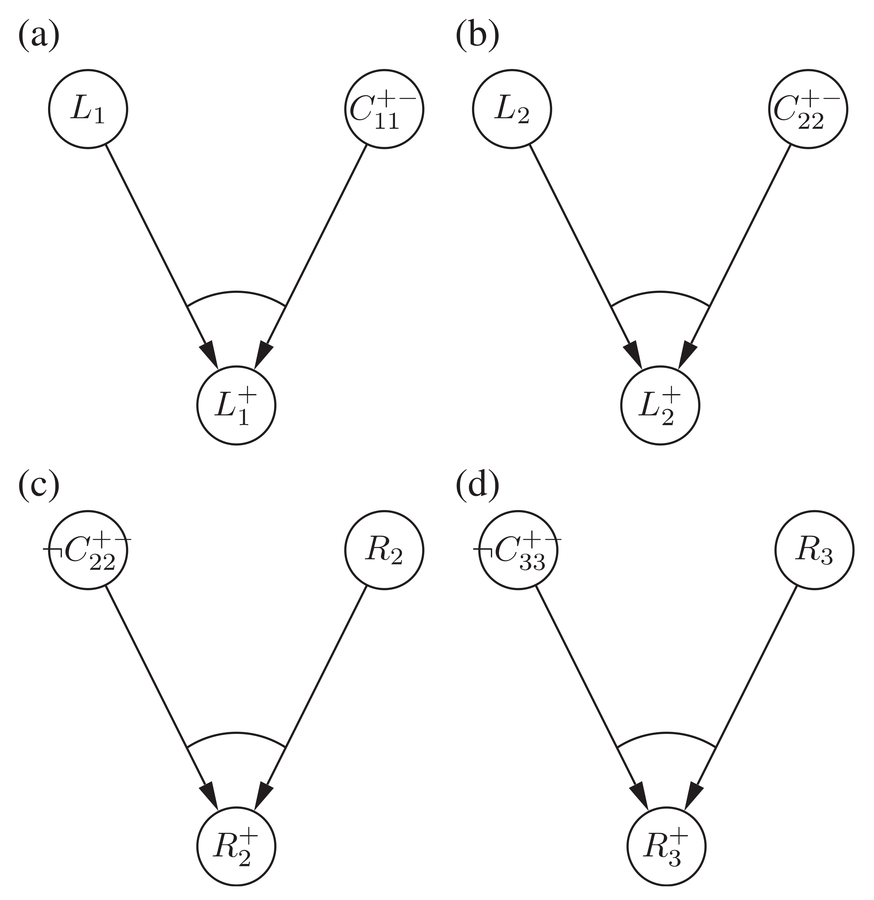
Fig. 1: Four graphical representations of complex sufficient conditions, following Graßhoff et.al. 2005. Cf. causal graphs in the sense of Baumgartner 2006, 73–79.
From these conditionals, we can derive the relative frequencies of the outcomes in terms of the relative frequencies of the screener-offs and the relative frequencies of the measurement operations. If we add the condition that the screener-offs are statistically independent from the measurement operations, we can even express the frequencies of the measurement outcomes in terms of only the screener-offs. That is, if we assume
• NO-CONS: The conjunction of the measurement operations and the conjunction of the screener-offs are statistically independent from each other:8
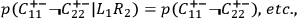
|
we have
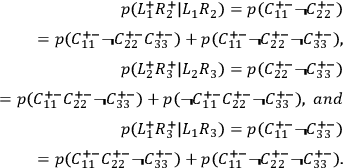
|
Because the right-hand side of the last equation contains only terms which also occur in the right-hand side of the previous two equations, the relative frequency which is expressed by the last equation cannot be larger than the sum of the other two frequencies, i. e.,
• BELL:
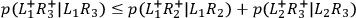 .
.
This is a version of Bell's inequality, which is violated significantly in the experiments which measure the relative frequencies to which the inequality refers.9 Therefore, we must conclude that at least one of the assumptions from which the inequality has been derived must be false.
3 Locality and Reality Conditions
According to my sketch of the detailed derivation of Bell's inequality, we need the assumptions of (i) perfect correlation, causal independence of the outcomes on each other (ii) and on the distant measurement operations (iii), (iv) the principle of the common cause, and (v) the statistical independence of the common causes on the measurement operations. That is, the following entailment holds:
PCORR & C-OI & C-PI & SCR & NO-CONS
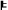 BELL
BELL
We performed the derivation in two steps, the first being the derivation of sufficient conditions for the measurement outcomes (SUFF), from the perfect correlations between causally independent outcomes (PCORR, C-OI), using a variant of the principle of the common cause (SCR):
PCORR & C-OI & C-PI & SCR
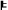 SUFF
SUFF
Using the intermediate conclusion SUFF, we proceeded, in a second step, to the derivation of Bell's inequality (BELL) from the causal independence of the outcomes on the distant measurement operations (C-PI), and the statistical independence of the screener-offs and the measurements operations:
C-PI & NO-CONS & SUFF
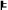 BELL
BELL
This entailment shows us that we cannot maintain SUFF without giving up at least one of C-PI or NO-CONS. If SUFF, i. e. the existence of sufficient conditions for the outcomes, is our notion of “realism” any “realistic” account of the quantum correlations in question will have to feature a causal dependence of the outcomes on the distant measurement operations or a statistical dependence between the measurement operations and the “elements of reality,” understood as the screener-offs of the perfect correlations:
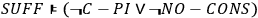
|
However, the first step of our derivation shows us that even if we are willing to give up “realism” in the sense of sufficient conditions for the outcomes, we still have to give up either C-OI, C-PI or SCR, or deny that the empirical evidence lends itself to the description as perfect correlations of the outcomes with parallel measurement settings.
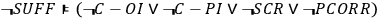
|
Therefore, giving up realism (understood as SUFF) does not help us as much as it might seem at first sight in avoiding the possible conflict between quantum mechanical phenomena, such as the EPR experiment, and the special theory of relativity. When considering the advantages of giving up “realism,” we should not only take into account the costs of maintaining it but also the costs that we nonetheless have to carry if we do give it up.
Understood along these lines, Maudlin's and Albert's and Galchen's critical remarks are to the point. However, the way they phrase the critique has several unattractive consequences.
If they maintain that the derivation of Bell's inequality is a reductio argument against locality conditions alone, they must subsume all of C-PI, NO-CONS, C-OI, SCR, and PCORR under their notion of locality. Also, if they regard the first step of the derivation as a variant of EPR's argument, which derives Realism from Locality, and the second step, “Bell's theorem” in their terms, as a derivation of Bell's inequality from Locality and Realism, the notion of locality in the first and the second step of the derivation is not necessarily the same. In the first step, “Locality” must entail the causal independence of the measurement outcomes and the version of the principle of the common cause:10
LOCEPR
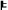 C-OI & C-PI & SCR
C-OI & C-PI & SCR
In the second step, “Locality” must entail the causal independence of the outcomes on the distant measurement operations and the statistical independence of the measurement operations and the screener-offs:
LOCBELL
 C-PI & NO-CONS.
C-PI & NO-CONS.
In both steps, they must identify “Realism” with SUFF:
Realism
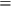 SUFF.
SUFF.
These consequences are unattractive mainly because assumptions such as NO-CONS or SCR have to be classified as “locality” conditions. Yet, NO-CONS, to begin with, is a condition relating event types which are instantiated by time-like separated events, whereas I take the usual referents of locality conditions to be event types which are instantiated by space-like separated events.11
Also SCR is not a particular statement about space-like separated events. Rather, it applies to any two types of events and says that there cannot be a correlation between them when they do not cause each other or when there is no screener-off of the correlation.
Of course, from a logical point of view, one can define whatever one pleases as long as the definitions are consistent. But in order to relate the discussion about the consequences of the empirical violation of Bell's inequality to the more general concepts of “locality” and “realism” we are well advised to link the premises of the derivation as closely as we possibly can to the meaning these terms have in their typical use. And on this measure, there is a much better alternative than the broad notion of locality which includes virtually any premise of Bell's inequality.
The alternative is to identify NO-CONS and SCR with “Realism,” i. e.,
Realism
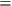 NO-CONS & SCR,
NO-CONS & SCR,
and C-OI and C-PI with “Locality”:
Locality
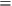 C-OI & C-PI.
C-OI & C-PI.
Like this, on the one hand, the locality conditions state particular cases of the prohibition that an event type be causally relevant for another event type when their coinciding instances are space-like separated. On the other hand, the realism conditions spell out the intuition “that there has to be something” accounting for our observations, and that this “something” is there, independent of our eventual measurement operations.
4 Thinking About Local, “Non-Realistic” Models
The previous analysis opens up the possibility, contra Maudlin, Albert, and Galchen, of maintaining locality and giving up realism instead. Local, “non-realistic” models would satisfy both C-PI and C-OI, but not both NO-CONS and SCR.
Models which violate only NO-CONS will have to address delicate, though perhaps not unresolvable, issues involving backward in time causation,12 or a hitherto unknown class of causal relations between the measurement operations and the events which are associated with the production of quantum mechanical singlet states.
Models which violate SCR are the other local but non-realistic option. These models will have to allow correlations between events which do not cause each other and which do not have a screener-off. However, whether such correlations can exist, is a question which has to do with our notion of causality, and the answer to this question is logically independent from the requirement that space-like separated events do not cause each other.
Acknowledgments
Research for this article was supported by the Swiss National Science Foundation under the grant no. 105211-129730 (principal investigator Gerd Graßhoff). A generous postdoctoral fellowship (Sept. 2011 – Apr. 2012) from the University of Pittsburgh's Center for Philosophy of Science gave me a particularly encouraging opportunity to write up these results.
References
Albert, David Z., Rivka Galchen (2009). A Quantum Threat to Special Relativity. Scientific American 3: 26-33
Aspect, Alain (2007). To Be or Not to Be Local. Nature 446: 866-867
Aspect, Alain, Jean Dalibard, J. D. (1982). Experimental Test of Bell's Inequalities Using Time-Varying Analyzers. Physical Review Letters 49(25): 1804-1807
Baumgartner, Michael (2006) Complex Causal Structures. Extensions of a Regularity Theory of Causation. phdthesis. University of Bern
- (2008). Regularity Theories Reassessed. Philosophia 36: 327-354
Bell, J. (1964). On the Einstein-Podolsky-Rosen paradox. Physics 1: 195-200
Bohm, D. (1951). Quantum Theory. New York: Prentice Hall.
Cushing, J.T., E. McMullin (1989). Philosophical Consequences of Quantum Theory: Reflections on Bell's Theorem..
Einstein, A., B. Podolsky, B. P. (1935). Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?. Physical Review 47(10): 777-780
Fraassen, Bas C. (1982). The Charybdis of Realism: Epistemological Implications of Bell's Inequality. Synthese 52(1): 25-38
Graßhoff, G., S. Portmann, S. P. (2005). Minimal Assumption Derivation of a Bell-type Inequality. The British Journal for the Philosophy of Science 56(4): 663-680
Graßhoff, Gerd, Michael May (2001). Causal Regularities. In: Current Issues in Causation Ed. by Wolfgang Spohn, M. Ledwig, M. L.. 85-114
Mackie, J. L. (1974). The Cement of the Universe: A Study of Causation. Oxford: Clarendon Press.
Maudlin, Tim (2002). Quantum Non-Locality and Relativity: Metaphysical Intimations of Modern Physics..
Price, Huw (1996). Time's Arrow and Archimedes' Point: New Directions for the Physics of Time..
Reichenbach, Hans (1956). The Direction of Time..
Wigner, Eugene P. (1970). On Hidden Variables and Quantum Mechanical Probabilities. American Journal of Physics 38(8): 1005-1009
Footnotes
The inequality is named after John Bell 1964, who derived it in 1964. The volume by Cushing and McMullin 1989 includes some of the first influential discussions of the philosophical implications of the inequality.
See Maudlin 2002 for a detailed discussion of the extent to which non-local interactions are incompatible with the theory of special relativity.
Einstein et.al. 1935; see also Bohm 1951.
See, e.g., Graßhoff et.al. 2005 for details.
By the symbols
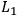 ,
,
 , and
, and
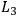 , I denote, respectively, the statements
that the measurement apparatus in the left wing of the experiment is set
to measure the spin in the first, second, or third direction.
, I denote, respectively, the statements
that the measurement apparatus in the left wing of the experiment is set
to measure the spin in the first, second, or third direction.
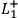 ,
,
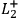 , and
, and
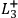 denote that the outcome of a spin measurement
in the left wing of the experiment in the first, second, or third direction
has the outcome “spin up.”
denote that the outcome of a spin measurement
in the left wing of the experiment in the first, second, or third direction
has the outcome “spin up.”
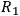 ,
,
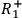 etc. denote the corresponding statements for the right wing of the experiment.
etc. denote the corresponding statements for the right wing of the experiment.
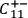 ,
,
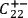 , and
, and
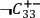 denote, respectively, the statements that
the screening-off event for the correlation between
denote, respectively, the statements that
the screening-off event for the correlation between
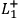 and
and
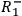 ,
,
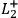 and
and
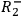 , or
, or
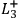 and
and
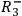 are instantiated in a given run of the experiment.
are instantiated in a given run of the experiment.
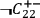 and
and
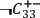 mean, respectively, that
mean, respectively, that
 or
or
 is not instantiated.
is not instantiated.
For details, see, e.g., Baumgartner 2008, 342.
Alternative causes for the outcomes are not represented and not discussed here.
I use
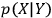 to denote the conditional probability of an
instantiation of events
of type
to denote the conditional probability of an
instantiation of events
of type
 , given that an event of type
, given that an event of type
 is instantiated.
is instantiated.
In this form, the inequality is discussed, e.g., by Fraassen 1982, and has probably first been derived by Wigner 1970. The first significant empirical violation of Bell's inequality has been observed by Aspect et.al. 1982.
I do not include PCORR in LOCEPR because it reflects idealized empirical data and is not meant by anyone to qualify as a locality or reality condition. For the present purposes, it is best seen as an auxiliary assumption.
Space-like separation of two events means that they happen far apart from each other and very soon one after the other or even simultaneously; in fact, the spatial distance divided by the temporal distance is larger than the speed of light, for space-like separated events. For time-like separated events, the spatial distance divided by the temporal distance is smaller than the speed of light. According to the theory of special relativity, the temporal order of space-like separated events depends on the frame of reference. Therefore, one is usually reluctant to admit causal dependence between two space-like separated events; in some frames of reference, the cause would happen after its effect.
See, e.g., Price 1996.
