Shortly after the end of the Great War,
[P]hysics and applied mathematics here are in an awful state. I am doing my inadequate best to talk to people about quanta; everybody accepts them here now (which is better than it was in 1914 at any rate), but I don’t think most of them realize their fundamental importance or have studied the arguments in connection with them […]. There are plenty of very intelligent people, only under the blighting influence of studying such things as strains in the ether, they none of them know what it is worth doing.1
By 1927 things had changed. The “Mathematical Tripos” (MT) and the “Natural Science Tripos” (NST) not only included a number of courses on quantum matters, but students taking these subjects were expected to respond to questions that, only some months earlier, had troubled the best scientific minds. To give an example, in the spring of 1928, one of the questions in the final exams was the following: “Show how the Heisenberg matrix of a
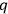 -number is determined from the normalized Schrödinger characteristic functions (Eigenfunktionen) of the problem concerned. Illustrate it by the problem of the rigid rotator (molecule).”2 This question expected an understanding not only of
-number is determined from the normalized Schrödinger characteristic functions (Eigenfunktionen) of the problem concerned. Illustrate it by the problem of the rigid rotator (molecule).”2 This question expected an understanding not only of
How did this change come about? The development of quantum physics and early quantum mechanics is a story that skips Cambridge and, generally, the British world. The first main English actor,
Here, I contribute to the early history of quantum physics in Cambridge by directing attention to the pedagogical side of the story. In particular, I concentrate on two books written by a quite-unknown Cambridge don, George Birtwistle (1877–1929). A senior wrangler in 1899, Birtwistle was fellow and lecturer of mathematics at Pembroke College and lectured on quantum physics and quantum mechanics between 1924 and 1929, producing two books that comprise his lectures. These two books present a number of interesting aspects. First, they help us understand the way a generation trained in the old wrangler tradition could understand and teach quantum theory. Second, they characterize the content that non-specialists in Cambridge received about the new physics. And third, they embody the tensions experienced by lecturers and students of the quantum theory at a time when it was developing and transforming rapidly.3

College, Cambridge.
Fig. 9.1: George Birtwistle. By permission of the Master and Fellows of Pembroke
College, Cambridge.
In the first section (9.1), I review British scientists’ early responses to quantum physics. The 1913 meeting in Birmingham of the British Association for the Advancement of Science (BAAS) was the first major public event in Britain in which positions in favor and against the theory of the quanta were discussed at length.
9.1 James Jeans and His Report on Radiation and the Quantum-Theory
The first written reference to Planck’s hypothesis in the British scientific milieu was probably
The Report on Radiation and the Quantum-Theory that
The Report is an interesting exercise of rhetoric, intended to convince British mathematical physicists, mostly influenced by the MT Cambridge tradition, of the unavoidability of the quantum hypothesis. From the beginning of the book,
[T]he mere discovery that a phenomenon is difficult to explain in the Newtonian way is no adequate reason for abandoning a system of laws which is known to hold throughout vast regions of natural phenomena […]. From demonstrating that a matter is difficult to proving that it is impossible is a long step, but if this step can be taken with respect to the explanation of even one well-established phenomenon of Nature, then the logical necessity of rejecting the impossibility becomes unanswerable. (Jeans 1914, 2)
The tendency in Britain at the time was to follow in
To understand the Report, we have to bear in mind the mental framework of the public to which it was addressed, a framework which Jeans himself had, until very recently, fully shared, and which had its roots in the metaphysics embedded in the training of Cambridge mathematical physicists. The ether was a real substance—and this remains so in the Report—and physical explanation was synonymous with mechanical modeling. These two aspects were pivotal in the introductory chapter:
For whatever is regarded as certain or uncertain about the ether, it must be granted as quite certain that it approaches more closely to a continuous medium than to a gas […]. And if, as seems most probable, the ether is a perfectly grainless structure, […] the total energy [in a black-body] will be infinite. […] To put the matter shortly: in all known media there is a tendency for the energy of any systems moving in the medium to be transferred to the medium and ultimately to be found, when a steady state has been reached, in the shortest vibrations of which the medium is capable. This tendency can be shown (Chapter II) to be a direct consequence of the Newtonian laws. This tendency is not observed in the crucial phenomenon of radiation; the inference is that the radiation phenomenon is determined by laws other than the Newtonian laws. (Jeans 1914, 6–7)
In support of the latter, chapter 2 partly repeats
Chapters 3 to 6 give a very clear account of the quantum theory and its success in accounting for radiation, spectra, the photoelectric effect, and the specific heat of solids (in this order), leaving for the last chapter what he calls the “physical difficulties” or the “physical basis” of the theory (Jeans 1914, 33 and 79). And this is the chapter to which I now turn, because it is here that we find
The indications are that there is, underlying the most minute processes of nature, a system of mechanical laws different from the classical laws, expressible by equations in which probably the quantum-constant h plays a prominent part. But these general equations remain unknown, and at most all that has been discovered is the main outline of the nature of these equations when applied to isochronous vibrations. (Jeans 1914, 79)
The main problem for Jeans was not that the quantum theory was, as yet, limited in its applicability, but that “even if the complete set of equations were known, it might be no easy task to give a physical interpretation of them, or to imagine the mechanism from which they originate” (Jeans 1914, 79, emphasis added). I emphasize the last sentence because, for him, as for most physicists of the Cambridge school, intelligibility involved the possibility of imagining a mechanism that could account for the observed phenomena. But when faced with the quantum, any “attempt to imagine a universe in which action is atomic leads the mind into a state of hopeless confusion” (Jeans 1914, 79–80).
From dimensional considerations,
[T]he brilliant agreement […] with experiment may indicate that in these cases the angular momentum of the single electron certainly behaves as though it were atomic, but this does not carry us any perceptible distance towards a physical explanation of why this atomicity exists. (Jeans 1914, 80)
More interesting for  e should not exist” (Jeans 1914, 81). And, although the atomicity of the charge did not necessarily involve the quantum theory, “otherwise the quantum theory would have been fully developed long ago […] there is, perhaps, a hope that the two atomicities may be special aspects of some principle more general than either of them” (Jeans 1914, 81); and this had to be, inevitably, related to the structure of the ether.
e should not exist” (Jeans 1914, 81). And, although the atomicity of the charge did not necessarily involve the quantum theory, “otherwise the quantum theory would have been fully developed long ago […] there is, perhaps, a hope that the two atomicities may be special aspects of some principle more general than either of them” (Jeans 1914, 81); and this had to be, inevitably, related to the structure of the ether.
The incorporation of
This last chapter finishes with a discussion on the reality of the ether, acknowledging that, in this respect, continental and British physicists play on different—opposed—sides. Jeans seems to cling to the reality of the ether, but he relegates it to a second place: the real stumbling block being the contradiction between discrete and continuous theories, both valid for different radiation phenomena. And, with this, the last pages of the book convey a certain amount of pessimism as to the status quo of physics. In a free translation from
It is impossible at present to predict the final issue. Will some entirely different solution be found? Or will the advocates of the new theory succeed in removing the obstacles which prevent us accepting it without reserve? Is discontinuity destined to reign over the physical universe, and will its triumph be final? Or will it finally be recognized that this discontinuity is only apparent, and a disguise for a series of continuous processes? […] Any attempt at present to give a judgement on these questions would be a waste of paper and ink. (Jeans 1914, 90)
While chapters 2 to 6 were an active exercise in convincing the reader of the inevitability of the quantum hypothesis and its successes, these last pages blunt that optimism by pointing to the difficulties of interpretation of the quantum theory. But this is done in a particular way: these last sentences can be interpreted as a way to encourage British physicists to embrace the theory rather than a priori rejecting it on the grounds that it is not “physical,” that is, mechanical. Furthermore, the fact that these considerations appear only at the end of the book as a separate chapter may indicate that, from Jeans’s point of view, one could and should accept the quantum theory without having a full answer to its ultimate physical meaning. Partly following the problem-solving tradition of the Cambridge MT pedagogy,
9.2 Teaching Quantum Theory in the 1920s
As mentioned in the introduction, the position of quantum theory in Cambridge was far from satisfactory at the end of the Great War. In 1920,
This chapter can of necessity provide only a very brief introduction into the mysteries of Quantum Dynamics, but I hope it will be of value in stimulating the interest of English-speaking readers in a branch of science of which the development has so far been left mainly to other nations. (Jeans 1921, preface to the third edition)
One way to track the status and evolution of the quantum in the old university is to have a look, however quick, at the evolution of courses taught to undergraduates. The “advanced,” optional courses were normally a reflection of the particular interests of individual researchers, and could give rise to exam questions only in what was known as Schedule B of the Tripos, Part II.4
It should be remembered that, following a tradition going back to the 1860s, physics in the 1920s was taught as part of the “Mathematical Tripos” (as theoretical physics or applied mathematics) and as part of the “Natural Science Tripos” (which was mainly experimental science). This meant that these two worlds were relatively independent of each other: experimental physics being taught at the Cavendish Laboratory, and mathematical physics by college lecturers. However, the special optional courses were, for the most part, open to both kinds of students.
Who could teach quantum theory in Cambridge? Certainly not people like
When Darwin left Cambridge in 1922, Fowler began to teach quantum physics, this time in courses open to both triposes. Unlike
In the academic year 1924/1925, we see a turning point in the teaching of quantum theory in Cambridge.
The following is a list of all these courses taken from the information provided in the Cambridge University Reporter in the period 1919–1929:
| 1920/21 | NST | Darwin: 1st Term, “Recent Developments in Spectrum Theory” |
| 1921/22 | MT | Darwin: 2nd Term, “The theory of quanta” |
| 1922/23 | MT & NST | Fowler: 2nd Term, “The quantum theory of spectra” |
| 1923/24 | MT & NST | Fowler: 2nd and 3rd Terms, “The quantum theory of spectra” |
| 1924/25 | MT & NST | Birtwistle: 2nd Term, “Introduction to the Quantum Theory” Fowler: 3rd Term, “The Quantum Theory. Recent Developments” |
| 1925/26 | MT & NST | Birtwistle: 1st Term, “Introduction to Quantum Theory” 2nd Term, “Quantum theory of Spectra” 3rd Term, “The Quantum Theory. Special Topics” Dirac: 3rd Term, “Quantum Mechanics (Recent Developments)” Hartree: 2nd Term, “Physics of the Quantum Theory” |
| 1926/27 | MT & NST | Birtwistle: 1st Term, “Quantum Theory” 3rd Term, “Quantum Mechanics,” (cont.) Hartree: 2nd Term, “Physics of the Quantum Theory” |
| 1927/28 | MT & NST | Birtwistle: 1st Term, “Quantum Theory of Spectra” 2nd Term, “The New Quantum Mechanics” Dirac: 1st Term, “Modern Quantum Mechanics” 2nd Term, “Modern Quantum Mechanics,” (cont.) Fowler: 3rd Term, “Statistical Mechanics, Old and New” Hartree: 2nd term, “Physics of the Quantum Theory” |
| 1928/29 | MT & NST | Birtwistle: 1st Term, “Quantum Theory of Spectra” 3rd Term, “Quantum Mechanics” Dirac: 2nd Term “Modern Quantum Mechanics” Fowler: 3rd Term, “Selected Problems in Wave Mechanics” Hartree: 2nd Term, “Physics of the Quantum Theory” 3rd Term, “Physics of the Quantum Theory,” (cont.) |
Tab. 9.1: List of all courses announced in the Cambridge University Reporter in the period 1919–1929.
Tab. 9.1: List of all courses announced in the Cambridge University Reporter in the period 1919–1929.
The only outsider named in the list of lecturers teaching quantum physics is Birtwistle, to whom the rest of this paper is devoted. And I say outsider not because he came from some other university, but because he was the only “real” wrangler accepting and spreading quantum physics in Cambridge, which makes him a unique example in trying to understand the ways in which the new theory was received in the old Cambridge wrangler tradition.
Birtwistle is a typical product of the MT tradition. Born in 1877, he arrived in Cambridge in 1895 and was bracketed senior wrangler in 1899. This means that he was a contemporary of
As a lecturer, Birtwistle was admirably clear and easy to follow. He set, in fact, a standard of exposition which made it very difficult for anyone to attract students to any duplicate course. His books are like his lectures—admirable expositions of those sections of the subject with which he deals, written in lecture-room style. He seldom attempts to go deeply into difficult points or to present the subject as a single logical whole. His aim is the lecturer’s aim—to interest the student in the subject, especially in its more outstanding or exciting parts, and lead him on to other more systematic or abstruse expositions. (Anonymous 1929, 881)
What courses did he normally teach? In the annual lists, we find him consistently teaching the general introductory courses on “Mechanics (Statics and Particle Dynamics; Rigid Dynamics)” and “Electricity,” and he was among the first to take on board courses on thermodynamics when these were introduced in the list of elementary courses in 1924. As for his more specialized courses, between 1920 and 1924, he consistently taught a one-term course on “Hydrodynamics (motion of solids and vortices in a liquid; waves).” In the academic year 1924/1925, he started teaching an “Introduction to Quantum Theory,” while Fowler taught more advanced quantum matters. In the following years, he taught further quantum courses, from which he finally produced two books: The Quantum Theory of the Atom in 1926, and The New Quantum Mechanics in 1928.
9.3 The Quantum Theory of the Atom
The Quantum Theory of the Atom is a window into Birtwistle’s first courses on quantum physics, in the early months of 1925, and in the academic year 1925/1926. It consists of a compilation of lectures from that period, and it was intended as a textbook for a similar course the following year (1926/1927). As is obvious from his correspondence with the publisher, Birtwistle rushed the printing of the book for two reasons: “as you know the subject is changing so rapidly that it would be a good thing to get it out as soon as possible; also so far there is no English book of this kind so far published and I think it will meet a real demand.”6 This book does not try to give a full, consistent, and closed picture of quantum physics, but rather to teach the mathematical apparatus needed to apply quantum physics, as known at the time. That means that the book is organized around the quantization strategy and its application to those cases for which it works. For the conceptually-minded reader, however, the book is disappointingly flat. Contrary to what happened with
But before we go into these and other technical elements, there is an aspect of the book, present especially in the more historical first two chapters, of particular interest. Birtwistle links the history of quantum physics to developments by British, especially Cambridge, scientists. The Quantum Theory of the Atom describes precisely that: the quantum theory of the structure of the atom, and this is a story that, according to Birtwistle, has its beginnings in Cambridge: “the modern theory of the structure of the atom is in the first place due to 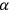 -particle was used to disclose the nature of the atom” and to propose an atomic model “which is now generally used in theoretical work” (Birtwistle 1926, 17). This model, for instance, is used to explain the nature of Thomson’s positive rays.
-particle was used to disclose the nature of the atom” and to propose an atomic model “which is now generally used in theoretical work” (Birtwistle 1926, 17). This model, for instance, is used to explain the nature of Thomson’s positive rays.
In this historical survey, 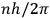 where
where
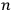 is an integer, while the latter gave the “new concept which was to be the key to the solution of the problem of spectra,” namely that “the radiation emitted between transitions between two stationary states has a frequency
is an integer, while the latter gave the “new concept which was to be the key to the solution of the problem of spectra,” namely that “the radiation emitted between transitions between two stationary states has a frequency
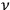 given by the relation
given by the relation
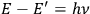 ” (Birtwistle 1926, 23). Throughout the book, however, Birtwistle keeps the expression “the Nicholson-Bohr condition,” meaning the nuclear model with quantized orbits. For the reader, this British-oriented story consolidates the idea that it was the “amazing verification” of
” (Birtwistle 1926, 23). Throughout the book, however, Birtwistle keeps the expression “the Nicholson-Bohr condition,” meaning the nuclear model with quantized orbits. For the reader, this British-oriented story consolidates the idea that it was the “amazing verification” of
The third chapter is a compilation of things that are related to the quantum theory but that are not dealt with in detail in the book. First is the one-page explanation of the mathematics of
Einstein’s theory of “light quanta” is not now generally accepted by physicists, but the argument above does not essentially depend upon their existence. All that is necessary is to assume that interchanges of energy between radiation and atoms can only occur in quanta. (Birtwistle 1926, 35–36)
If we remember that the book was written in 1926, this paragraph is somewhat surprising since, by then, the experiments of
Having established the existence, historical origin, and realm of application of the new theory, the rest of the book is an attempt to train students in techniques of quantization using a twofold strategy: to provide lots of examples where quantization is successfully applied, and to show that there is continuity between the methods used in “classical” and quantum theory. Because, as Birtwistle sees it, that is the only way one gets hold of the new physics: by using it, rather than by presenting it in a general form or analyzing its conceptual or philosophical implications. And this brings us to the main claim of this paper. Birtwistle, a first wrangler in the “Mathematical Tripos,” tried to teach quantum physics in the same way classical physics was taught in the Cambridge MT tradition: by repetition of examples, by solving specific problems, and by a relatively uncritical embrace of particular mathematical methods.
Once 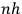 for more complex systems than that of the hydrogen atom.” The answer was given by
for more complex systems than that of the hydrogen atom.” The answer was given by
[T]hat the “entity” which does not change under the influence of the slowly changing external forces must be an “adiabatic invariant” of the classical theory. This is the “adiabatic principle” of Ehrenfest, and it requires that only adiabatic invariants are to be equated toin order to determine the stationary states. (Birtwistle 1926, 41)
With the generalization of the quantum condition, Birtwistle embarks on a series of chapters explaining what he calls the basic “general dynamical theory,” chapters in which he fully shows his conditioning as a wrangler. The variation principle,  , without further ado.
, without further ado.
As an example, we can pick chapter 9 on the
The dynamical problem to be solved is the motion of an electron due to a Coulomb center of force and a constant force parallel to a fixed direction. This is a particular case of two centers of force solved byJacobi by the use of elliptic coordinates. (Birtwistle 1926, 97–98)
All this he explains from an exclusively mathematical point of view. At the end of the process, the quantum condition (
 ) is imposed as part of a mathematical technique, through which the numerical results can be calculated and compared with experimental values. The reader is, thus, led to believe that quantum physics is in strict mathematical (and, therefore, physical) continuity with earlier physics, since the mathematical methods and formulas are almost the same.
) is imposed as part of a mathematical technique, through which the numerical results can be calculated and compared with experimental values. The reader is, thus, led to believe that quantum physics is in strict mathematical (and, therefore, physical) continuity with earlier physics, since the mathematical methods and formulas are almost the same.
It would be superfluous, in this paper, to give a detailed account of each chapter in Birtwistle’s book. The structure is basically the same for all: classical calculations in which the quantum condition is brought in as a particular mathematical trick that needs to be implemented to get a correspondence with experimental data. In 21 chapters, one can never find words such as “provisional,” “incomplete,” “failed explanation,” or anything that indicates that the quantum theory of the atom, as it is, might be viewed as incomplete or, worse, deficient. It is only in a rushed last chapter, written during what looks like his usual vacation in Norway,8 that Birtwistle introduces the reader to a list of unexplained phenomena like the
Only in the last two pages, and in a statement that de facto undermines the whole project of this book, does he say:
Heisenberg has lately put forward the beginnings of a scheme of quantum-kinematics, which when more developed should lead to the direct deduction of these quantum theory formulae, without the intermediate use of the classical formulae in each problem considered. (Birtwistle 1926, 230–231)
This undermining of his entire first book leads us very naturally to Birtwistle’s second book, to which the next section is devoted. But before we move on, it is worth noting that Birtwistle’s introductory course in quantum theory was substituting for
9.4 The New Quantum Mechanics
Birtwistle wrote a second book on quantum physics, related to his more advanced lectures on recent developments of quantum mechanics, the preface of which was signed in Copenhagen in October 1927.10 From a pedagogical point of view, The New Quantum Mechanics is very disappointing. Even in the respectful tone of an obituary, his biographer alluded to this fact:
Perhaps the least successful of his books was the last, on modern quantum mechanics. Here, owing to the novelty of the subject and the absence (when Birtwistle wrote) of other more systematic expositions (or indeed of any other exposition), the weakness of this deliberate method becomes more obvious. The book gives rather the impression of a collection of interesting isolated sketches. (Anonymous 1929, 881)
The New Quantum Mechanics is precisely that: a collection of the latest developments in quantum theory. In the words of another reviewer:
This account is very accurate and contains practically everything that has been done up to the summer of 1927. He gives us, so to speak, original abstracts of the principal papers and allows us a survey of everything that is known. This makes the work not exposition from one point of view, as isWeyl’s new book; it is rather an “impartial” treatment of the methods of the different schools, with credit given to each for its results. (Struik 1930, 32)
In Nature,
The first five chapters of this book provide further examples supporting my claims at the end of last section. Birtwistle’s “impartiality” involves a neutral style in the sense that there are no critical analyses of the theories, or their theoretical or experimental limitations. These first chapters introduce the notion of spin, for which he needs to explain the problem with the anomalous
The matter-of-fact style is clear from the first sentences of the book: “The origin of the new quantum mechanics was an epoch-making memoir by
[A] real difficulty too had been met with in the spectrum of neutral helium, where two electrons revolve round the nucleus (the simplest many electron problem), all the theoretical results found being at variance with experiment; again in the problem of the “crossed” fields, where an atom is exposed to the combined action of electric and magnetic fields, fundamental difficulties arose. (Birtwistle 1928a, 1)
Obviously, in his previous book, Birtwistle never talked about these very “fundamental” problems, or about the limitations of the now “old” quantum theory, which was, at the time, the accepted way to solve those problems. It is only in 1928, after a new method has been found, that the limitations of the previous method are relevant: 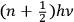 as the energy of the stationary state of Planck’s oscillator, so that half odd integers came quite naturally into the new results” (Birtwistle 1928a, 2).
as the energy of the stationary state of Planck’s oscillator, so that half odd integers came quite naturally into the new results” (Birtwistle 1928a, 2).
In the last chapter, Birtwistle tried to summarize his understanding of the latest, as yet unpublished, developments coming from Bohr’s institute. Returning from his holiday in Norway, Birtwistle visited Copenhagen, but
Prof. Bohr points out that the wording of the chapter may create the impression that these [probability] calculations were primarily developed in connexion with the new ideas [of complementarity], whereas they may be said to be characteristic of the whole recent developments of the quantum theory. (Birtwistle 1928b, 58)
Actually, the wording of this note was revised and changed by
One last, revealing anecdote about the book comes from William McCrea, who was an undergraduate in Cambridge between 1923 and 1926. Talking about The New Quantum Mechanics, he recalled that:
[I]t was a remarkable achievement to produce such a comprehensive account of work newly published during the two years before the appearance of the book itself.Hartree described it to me in conversation as the “bare bones” of the subject, but it need not be only medical students who find it useful to have a skeleton for their studies.12 (McCrea 1985, 58)
9.5 Conclusion
Contrary to
Birtwistle’s case can help us to understand another fact that is normally forgotten in the histories of revolutions. Quantum theory was not, for everyone, that revolutionary new theory that forced them into research. Birtwistle is an example of how one could, in times of change, stick to old methodological—not conceptual—paradigms. And, again, not all the students interested in quantum physics were necessarily potential participants in the forefront of scientific research. Having both
Abbreviations and Archives
| AHQP | Archive for History of Quantum Physics. American Philosophical Society, Philadelphia |
| BAAS | British Association for the Advancement of Science |
| Bohr Collection | Archive for History of Quantum Physics |
| Cambridge Tripos Examination Papers | Cambridge University Library |
| Cambridge University Press Archives | Manuscripts Department of the University Library at the University of Cambridge |
| Churchill Archives Centre | Churchill College, Cambridge |
| MT | Mathematical Tripos |
| NST | Natural Science Tripos |
References
Anonymous (1914). Discussion on Radiation. In: Report of the Eighty-Third Meeting of the British Association for the Advancement of Science. Birmingham: 1913, September 10-17 London: John Murray 376-386
- (1929). Obituary. Nature 123: 881
Birtwistle, George (1926). The Quantum Theory of the Atom. Cambridge: Cambridge University Press.
- (1928a). The New Quantum Mechanics. Cambridge: Cambridge University Press.
- (1928b). The Complementary Nature of the Quantum Theory. Nature 122: 58
Bohr, Niels (1918). On the Quantum Theory of Line Spectra. Det kongelige danske videnskabernes Selskab, matematisk-fysike Meddelelser 4(1): 1-36
Ewald, Paul P. (1913). Bericht über die Tagung der British Association in Birmingham (10. bis 17. September). Physikalische Zeitschrift 14: 1297-1302
Fowler, Ralph H. (1929). Review of . Nature 123: 363
Gavroglu, Kostas, Anna Simoes (2002). Preparing the Ground for Quantum Chemistry in Great Britain: the Work of the Physicist R. H. Fowler and the Chemist N. V. Sidgwick. British Journal for the History of Science 35: 187-212
Hudson, Rob (1989). James Jeans and Radiation Theory. Studies in History and Philosophy of Science 20: 55-77
Jeans, James (1904). The Dynamical Theory of Gases. Cambridge: Cambridge University Press.
- (1914). Report on Radiation and the Quantum-Theory. London: The Electrician.
- (1921). The Dynamical Theory of Gases. Cambridge: Cambridge University Press.
Larmor, Joseph (1909). The Statistical and Thermodynamical Relations of Radiant Energy. Proceedings of the Royal Society A 83: 82-95
Lodge, Oliver (1914). Presidential Address. In: Report of the British Association for the Advancement of Science, 1913 London: John Murray 3-42
McCormmach, Russell (1966). The Atomic Theory of John William Nicholson. Archive for History of Exact Sciences 3: 160-184
McCrea, William (1985). How Quantum Physics Came to Cambridge. New Scientist 96: 58-60
- (1987). Cambridge 1923–6: Undergraduate Mathematics. In: The Making of Physicists Ed. by Rajkumari Williamson. Bristol: Hilger 53-66
Milne, Edward A. (1952). Sir James Jeans. A Biography. Cambridge: Cambridge University Press.
Navarro, Jaume (2009). “A Dedicated Missionary.” Charles Galton Darwin and the New Quantum Mechanics in Britain. Studies in History and Philosophy of Modern Physics 40: 316-326
Robertson, Peter (1979). The Early Years. The Niels Bohr Institute, 1921–1930. Copenhagen: Akademisk Forlag.
Struik, Dirk J. (1930). Review of . The American Mathematical Monthly 37: 32
Warwick, Andrew (2003). Masters of Theory: Cambridge and the Rise of Mathematical Physics. Chicago: The University of Chicago Press.
Footnotes
Darwin to Bohr, 30 May 1919, BSC 1, 4, AHQP.
Cambridge Tripos Examination Papers.
In picturing the state of physics in Cambridge before and immediately after the Great War, I closely follow the analysis of Andrew Warwick (2003).
According to William McCrea, in his recollections of his undergraduate days in Cambridge:
Apparently anyone could offer to deliver a one-term lecture course. If the appropriate Faculty Board approved, it would be announced in the Schedule B lecture list. This implied that in due time a candidate could declare a wish for there to be questions (probably two) on the course in the examination […]. If any candidate legitimately included a particular course in his list, the lecturer was responsible for producing the questions; these had then to be approved by the Part II Examiners, who had to arrange the Schedule B papers in such a way that every candidate’s chosen subjects were suitably distributed through the six papers. But when it came to the examination any candidate could attempt any questions he liked; he need not confine himself to the topics in the list. (McCrea 1987, 62)
Fowler, Hartree, and Dirac were visitors at Bohr’s institute in Copenhagen.
Birtwistle to S. C. [sic], September 1926, Cambridge University Press Archives.
Nicholson was a Cambridge graduate, taught mathematical physics at the Cavendish Laboratory, and moved to King’s College, London, in 1912. For a full account of Nicholson’s work and influence on Bohr, see (McCormmach 1966).
Letters from Birtwistle to the secretary of Cambridge University Press testify to these holidays, 26 September 1926, 22 August 1927, 9 September 1927, Cambridge University Press Archives.
Microfilm no. 6, AHQP.
The official list of visitors does not include Birtwistle as a formal visitor to Bohr’s Institute (Robertson 1979, 156–158). Furthermore, in an epistolary exchange with Bohr, they both regret that they could not meet each other in Copenhagen during Birtwistle’s visit, from which I infer that his was more of a touristic visit than a research trip (microfilm no. 16a, AHQP).
Microfilm no. 9, Bohr Collection.
See also (McCrea 1987).
Fowler to Dirac, 12 June 1927, DRAC 3/1, Churchill College Archives.
