8.1 Outline
A little more than half a year before matrix mechanics was born, Max Born finished his book Vorlesungen über Atommechanik, Erster Band, which was a state-of-the-art presentation of
Max Born’s monograph Vorlesungen über Atommechanik, Erster Band, was published in 1925 by Julius Springer Verlag (Berlin) as volume II in the Series Struktur der Materie (Born 1925). The second volume of the Vorlesungen appeared in 1930 as Elementare Quantenmechanik, coauthored by
Here I will focus entirely on the first volume, which gave a state-of-the-art account of Bohr-Sommerfeld quantization from the analytic perspective. One might therefore suspect that the book had almost no impact on the post-1924 development3 of quantum mechanics proper, whose 1925–26 breakthrough did not originate from further analytical refinements of Bohr-Sommerfeld theory.4 But this would be a fruitless approach to Born’s book, which is truly remarkable in at least two aspects: First, for its presentation of analytical mechanics, in particular
8.2 Structure of the Book
The book is based on lectures Born gave in the winter semester 1923/24 at the University of Göttingen and was written with the help of Born’s assistant
The chapter contents are as follows:
1Introduction: Physical Foundations (3 sections, 13 Pages)
2Chapter 1: Hamilton-Jacobi Theory (5 sections, 23 pages)
3Chapter 2: Periodic and multiply periodic motions (12 sections, 81 pages)
4Chapter 3: Systems with a single valence (‘light’) electron (19 sections, 129 pages)
5Chapter 4: Perturbation theory (10 sections, 53 pages)
Both Vorlesungen über Atommechanik volumes were reviewed by
of which one cannot say, that the invested effort corresponds to the results achieved, which are, above all, mainly negative (invalidity of mechanics for the Helium atom). Whether this method can be the foundation of the true quantum theory of couplings, as the author believes, has to be shown by future developments. May this work itself accelerate the development of a simpler and more unified theory of atoms with more than one electron, the manifestly unclear character as of today is clearly pictured in this chapter.6 (Pauli 1925, 488)
As an amusing aside, this may be compared with
This book is the second volume of a series, in which each time the aim and sense [Ziel und Sinn] of the nth volume is made clear by the virtual existence of the (n+1)st. (Pauli 1930, 602)
Having given no recommendation, the review then ends with:
The making [Ausstattung] of the book with respect to print and paper is excellent [vortrefflich]. (Pauli 1930, 602)
8.3 Born’s Pedagogy and the Heuristic Role of the Deductive/Axiomatic Method
8.3.1 Sommerfeld versus Born
Wilhelm von Humboldt’s early nineteenth-century, programmatic vision of an intimate coexistence and cross-fertilization of teaching and research soon became a widely followed paradigm for universities in Prussia, in other parts of Germany, and around the world. And even though it is clear from experience that it cannot be a general rule that the best researchers make the best teachers, or vice versa, Humboldt’s program has nevertheless proven extremely successful. In fact, outstanding examples for how to put into action Humboldt’s maxim are provided by the Munich and Göttingen schools of Quantum Physics during the post-World-War-I period. Their common commitment to the “Humboldtian Ideal,” with actions that speak louder than words, resulted in multiple generations of researchers and teachers of the highest originality and quality. What makes this even more convincing is the impression that this was not achieved on account of individual exceptionality; quite the contrary.
This name [analytical mechanics] originated in the grand work ofLagrange’s of 1788, who wanted to clothe all of mechanics in a uniform language of formulae and who was proud that one would not find a single figure throughout his work. We, in contrast, will resort to intuition [Anschauung] whenever possible and consider not only astronomical but also physical and, to a certain extent, technical applications. (Sommerfeld 1977, Vorbemerkung)
The preface itself contains the following programmatic paragraph, which clearly characterizes
Accordingly, in print [as in his classes; D.G.] I will not detain myself with the mathematical foundations, but proceed as rapidly as possible to the physical problems themselves. I wish to supply the reader with a vivid picture of the highly structured material that comes within the scope of theory from a suitable chosen mathematical and physical vantage point. May there, after all, remain some gaps in the systematic justification and axiomatic consistency. In any case during my lectures I did not want to put off my students with tedious investigations of mathematical or logical nature and distract them from the physically interesting. This approach has, I believe, proven useful in class and has been maintained in the printed version. As compared to the lectures byPlanck, which are impeccable in their systematic structure, I believe I can claim a greater variety in the material and a more flexible handling of the mathematics. (Sommerfeld 1977, v–vi)
This pragmatic paradigm has been taken over and perfected by later generations of theoretical physicists; just think of the 10-volume lecture courses by
There are many things to be said in favor of this pragmatic approach. For one thing, it takes account of the fact that developing understanding is a cyclic process. Every serious student knows that one has to go over the same material again and again in order to appreciate the details of statements, the hidden assumptions, and the intended range of validity. Often, on one’s
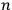 th iteration one discovers new aspects, in view of which one’s past understanding is revealed as merely apparent and ill-founded. Given that we can almost never be sure that this will not happen again in the future, one might even be tempted to measure one’s own relative degree of understanding by the number of times this has already happened in the past. From that perspective, the pragmatic approach seems clearly much better suited, since it does not pretend to the fiction of an ultimate understanding. Hence, being able to solve concrete
problems sounds like a reasonable and incorruptible criterion.
th iteration one discovers new aspects, in view of which one’s past understanding is revealed as merely apparent and ill-founded. Given that we can almost never be sure that this will not happen again in the future, one might even be tempted to measure one’s own relative degree of understanding by the number of times this has already happened in the past. From that perspective, the pragmatic approach seems clearly much better suited, since it does not pretend to the fiction of an ultimate understanding. Hence, being able to solve concrete
problems sounds like a reasonable and incorruptible criterion.
However, as
It is with regard to this question that I see a clear distinction between the approaches of Born and Sommerfeld.
Everything works out all right [klappt] and yet remains fundamentally unclear. I can only cultivate [fördern] the techniques of the quanta, you have to provide your philosophy. (Hermann 1968, 97)
Cultivating new seeds could start with establishing simple axioms in a well-defined mathematical framework. But even that might turn out to be premature.
At the current status of the theory it would be premature to start with a system of well defined axioms and then deduce from them the theory by means of exact mathematical methods. What one needs is a mathematical description which adequately describes the experimental situation, which does not seem to contain contradictions and which, therefore, might later be completed to an exact mathematical scheme. History of physics teaches us that, in general, a new theory can be phrased in a precise mathematical language only after all essential physical problems have been solved. (Heisenberg 1967, vi)
It seems even more obvious that, in phases of paradigmatic uncertainty, little help can be expected from attempts to establish an axiomatic framework for the doomed theory. And yet, surprisingly, this is precisely what Born did, as we shall see in the next subsection.
In a letter to
This dichotomy is not strictly exclusive. An obvious example of someone who could with equal right be located in both camps is
In Sommerfeld’s institute one learned to solve special problems; one learned the tricks, you know. Born took it much more fundamentally, from a very general axiomatic point of view. So only in Göttingen did I really learn the techniques well. Also in this way Born’s seminar was very helpful for me. I think from this Born seminar on I was able really to do perturbation calculations with all the rigor which was necessary to solve such problems. (Seth 2010, 58)
Let us now turn to how Born himself expresses the heuristic value of the axiomatic method in times of uncertainty.
8.3.2 A Remarkable Introduction
One third of the way through the book, Born recalls the basic idea of ‘Quantum Mechanics’ in the following way (the emphases are Born’s):
Once again, we summarize the basic idea of Quantum Mechanics, as developed so far: For a given Model [Modell] we calculate the totality of all motions (which are assumed to be multiply periodic) according to the laws of Classical Mechanics (neglecting radiation damping); the quantum conditions select a discrete subset from this continuum of motions. The energies of the selected motions shall be the true [wirkliche] ones, as measurable by electron collision, and the energy differences shall, according toBohr’s frequency condition, correspond [zusammenhängen] with the true [wirklichen] light frequencies, as observed in the spectrum. Besides frequencies, the emitted light possesses the observable properties of intensity, phase, and state of polarization, which are only approximately accounted for by the theory (§ 17). These exhaust the observable properties of the motion of the atomic system. However, our computation assigns additional properties to it, namely orbital frequencies and distances, that is, the course [Ablauf] of motion in time. It seems that these quantities are, as a matter of principle, not accessible to observation.8 Therewith we arrive at the following judgement [Urteil], that for the time being our procedure is just a formal computational scheme which, for certain cases, allows us to replace the still unknown quantum laws by computations on a classical basis [auf klassischer Grundlage]. Of these true [wahren] laws we would have to require, that they only contain relations between observable quantities, that is, energy, light frequencies, intensities, and phases. As long as these laws are still unknown, we have to always face the possibility that our provisional quantum rules will fail; one of our main tasks will be to delimit [abgrenzen] the validity of these rules by comparison with experience. (Born 1925, 113–114)
As an (obvious) side remark, we draw attention to the
similarity between Born’s formulations in the second half
of the above cited passage and
Born’s book attempts an axiomatic-deductive approach to
The title ‘Atommechanik’ of this lecture, which I delivered in the winter-semester 1923/24 in Göttingen, is formed after the label ‘Celestial Mechanics.’ In the same way as the latter labels that part of theoretical astronomy which is concerned with the calculation of trajectories of heavenly bodies according to the laws of mechanics, the word ‘Atommechanik’ is meant to express that here we deal with the facts of atomic physics from the particular point of view of applying mechanical principles. This means that we are attempting a deductive presentation of atomic theory. The reservations, that the theory is not sufficiently mature [reif], I wish to disperse with the remark that we are dealing with a test case [Versuch], a logical experiment, the meaning of which just lies in the determination of the limits to which the principles of atomic and quantum physics succeed, and to pave the way which shall lead us beyond those limits. I called this book ‘Volume I’ in order to express this program already in the title; the second volume shall then contain a higher approximation to the ‘final’ mechanics of atoms.
I am well aware that the promise of such a second volume is daring [kühn]; since presently we have only a few hints as to the nature of the deviations that need to be imposed onto the classical laws in order to explain the atomic properties. To these hints I count first of allHeisenberg’s rendering of the laws of multiplets and anomalous Zeeman effect, the new radiation theory of Bohr, Kramers, and Slater, the ensuing Ansätze of Kramers for a quantum-theoretic explanation of the phenomena of dispersion, and also some general considerations concerning the adaptation of perturbation theory to the quantum principles, which I recently communicated. But all this material, however extensive it might be, does not nearly suffice to shape a deductive theory from it. Therefore, the planned ‘2. Volume’ might remain unwritten for many years to come; its virtual existence may, for the time being, clarify the aim and sense [Ziel und Sinn] of this book. (Born 1925, v–vi)
Born continues and explicitly refers to (and suggests the reading of) Sommerfeld’s Atombau und Spektrallinien, almost as a prerequisite for a successful study of his own book. But he also stresses the difference, which lies in part in the deductive approach:
For us the mechanical-deductive approach always comes first [steht überall obenan]. Details of empirical facts will only be given when they are essential for the clarification, the support, or the refutation of theoretical strings of thought [Gedankenreihen]. (Born 1925, vi)
But, Born continues, there is a second difference from Atombau und Spektrallinien, namely with respect to the foundations of quantum theory, where
differences in the emphasis of certain features [Züge] are present; but I leave it to the author to find these out by direct comparison. As regards the relation of my understanding to that of Bohr and his school, I am not aware of any significant opposition. I feel particularly sympathetic with the Copenhagen researchers in my conviction, that it is a rather long way to go to a ‘final quantum theory.’ (Born 1925, vi)
It would be an interesting project to try to work out the
details of the “second difference,” concerning the foundations
of quantum theory, by close comparison of Born’s text with
Atombau und Spektrallinien. Later, as we know, Born in principle
favored the more abstract algebraic approach (
Born ends his introduction by acknowledging the help of several
people, foremost his assistant
Here I specifically mention the theorem concerning the uniqueness of action-angle variables which, according to my view, lies at the foundation of today’s quantum theory; the proof worked out by Hund forms the centre [Mittelpunkt] of the second chapter (§ 15). (Born 1925, vii)
Hund is also thanked for the presentation of
8.4 On Technical Issues: What Is Quantization?
A central concern of Born’s book is the issue of quantization rules, that is: How can one unambiguously generalize
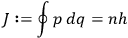
|
8.1 |
to systems with more than one degree of freedom?
The history of attempts to answer this question is
interesting, but also rather intricate, and involves
various suggestions by
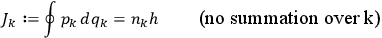
|
8.2 |
where
 labels the degrees of freedom
to be quantized, which need not necessarily exhaust all
physical degrees of freedom, of which there are
labels the degrees of freedom
to be quantized, which need not necessarily exhaust all
physical degrees of freedom, of which there are
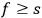 ,
as we shall discuss below.9 Here we adopt the notation from
Born’s book, where
,
as we shall discuss below.9 Here we adopt the notation from
Born’s book, where
 are
the generalized coordinates (configuration variables) and
momenta respectively. The apparent simplicity of
(8.2) is deceptive though. One thing
that needs to be clarified is the domain of integration implicit in the
are
the generalized coordinates (configuration variables) and
momenta respectively. The apparent simplicity of
(8.2) is deceptive though. One thing
that needs to be clarified is the domain of integration implicit in the
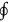 -symbol. It indicates that the
integration over
-symbol. It indicates that the
integration over
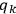 is to be performed over a full
period of that configuration variable.
In Sommerfeld’s words, emphasis in the original:
is to be performed over a full
period of that configuration variable.
In Sommerfeld’s words, emphasis in the original:
Each coordinate shall be extended over the full range necessary to faithfully label the phase of the system. For a cyclic azimuth in a plane this range isto
, for the inclination in space (geographic latitude
) twice the range between
and
, for a radial segment
[Fahrstrahl] likewise twice the covered interval from
to
for the motion in question. (Sommerfeld 1916, 7)
Another source of uncertainty concerns the choice of canonical
coordinates for which (8.2) is meant to
hold. Again in
Unfortunately a general rule for the choice of coordinates can hardly be given; it will be necessary to collect further experience by means of specific examples. In our problems it will do to use (planar and spatial) polar coordinates. We will come back to a promising rule of Schwarzschild and Epstein for the choice of coordinates in § 10. (Sommerfeld 1916, 6)
The rule that
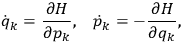
|
8.3 |
for time-independent Hamiltonians
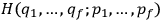 are solved by means
of a general solution
are solved by means
of a general solution
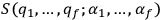 for the
Hamilton-Jacobi equation
for the
Hamilton-Jacobi equation
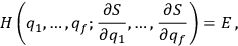
|
8.4 |
where
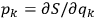 and
and
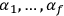 are constants of integration on which the energy
are constants of integration on which the energy
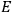 depends.
Second, and most important, is that this solution is obtained
by separation of variables:
depends.
Second, and most important, is that this solution is obtained
by separation of variables:
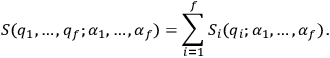
|
8.5 |
Note that this implies in particular that
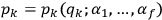 , i.e. the
, i.e. the
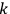 -th momentum only depends on the
-th momentum only depends on the
 -th configuration
variable and the
-th configuration
variable and the
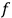 constants of integration
constants of integration
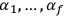 . This is indeed necessary for
(8.2) to make sense, since the right
hand side is a constant and can therefore not be meaningfully
equated to a quantity that depends nontrivially on phase space.
Rather, the meaning of (8.2) is to
select a subset of solutions through equations for the
. This is indeed necessary for
(8.2) to make sense, since the right
hand side is a constant and can therefore not be meaningfully
equated to a quantity that depends nontrivially on phase space.
Rather, the meaning of (8.2) is to
select a subset of solutions through equations for the
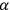 ’s.
However, separability is a very strong requirement indeed. In particular, it requires the integrability of the
dynamical system in question, a fact which only
’s.
However, separability is a very strong requirement indeed. In particular, it requires the integrability of the
dynamical system in question, a fact which only  have been introduced as so-called
‘action variables,’ which are conjugate to some
‘angle variables’
have been introduced as so-called
‘action variables,’ which are conjugate to some
‘angle variables’
 ; for then the action
variables constitute the
; for then the action
variables constitute the
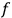 observables in involution, i.e.
their mutual Poisson brackets obviously all vanish.10
observables in involution, i.e.
their mutual Poisson brackets obviously all vanish.10
But even if we swallow integrability as a conditio sine qua non,
does separability ensure uniqueness? What is the strongest guarantee of
uniqueness
one can hope for? Well, for (8.2)
to make sense, any two allowed (by conditions yet to be formulated)
sets of canonical coordinates
 and
and
 must be such that the
must be such that the
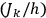 ’s
(calculated according to 8.2)
are integers if and only if the
’s
(calculated according to 8.2)
are integers if and only if the
 ’s are. This is
clearly the case if the allowed transformations are such
that among the action variables
’s are. This is
clearly the case if the allowed transformations are such
that among the action variables
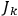 they amount to linear
transformations by invertible integer-valued
matrices:11
they amount to linear
transformations by invertible integer-valued
matrices:11

|
8.6a |
Here
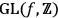 is the (modern) symbol for the group of invertible
is the (modern) symbol for the group of invertible
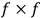 matrices with integer
entries. The most general transformations for the angle
variables compatible with (8.6a)
are
matrices with integer
entries. The most general transformations for the angle
variables compatible with (8.6a)
are
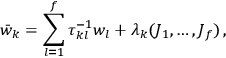
|
8.6b |
where the
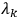 are general (smooth)
functions.12
are general (smooth)
functions.12
The task is now to carefully amend the
Born also states that the technical conditions under which
this result for multiply periodic systems can be derived
were already given in the unpublished thesis by
1A The position of the system shall periodically depend on
the angle variables
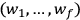 with primitive
period 1.
with primitive
period 1.
2B The Hamiltonian is transformed into a function
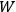 depending only on the
depending only on the
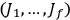 .13
.13
3C The phase-space function:
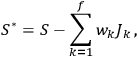
|
8.7 |
considered as function of the variables
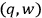 ,
which generates the canonical transformation
,
which generates the canonical transformation
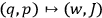 via
via
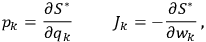
|
8.8 |
shall also be a periodic function of the
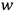 ’s with period 1.
’s with period 1.
A and B are immediately clear, but the more technical condition
C is not. And, as Born remarks, A and B do not suffice to lead
to the desired result. In fact, a simple canonical transformation
 compatible with A and B is
compatible with A and B is
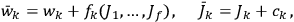
|
8.9 |
where the
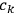 are arbitrary constants. Their possible
presence disturbs the quantization condition, since
are arbitrary constants. Their possible
presence disturbs the quantization condition, since
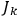 and
and
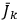 cannot, in general, both simultaneously be integer multiples of
cannot, in general, both simultaneously be integer multiples of
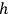 . Condition C now eliminates this
freedom. After some manipulations the following result
is stated:
. Condition C now eliminates this
freedom. After some manipulations the following result
is stated:
Theorem (Uniqueness for non-degenerate systems) If, for a mechanical system, variablescan be introduced satisfying conditions A-C, and if there exist no commensurabilities between the quantities
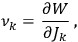
|
8.10 |
then the action variablesare determined uniquely up to transformations of type (8.6a) [that is, linear transformations by
]. (Born 1925, 104)
For the proof, as well as for the ensuing interpretation of
the quantization condition, the notions of degeneracy
and commensurability are absolutely essential: An
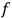 -tuple
-tuple
 of real numbers is called
of real numbers is called
 -fold
degenerate, where
-fold
degenerate, where
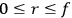 , if there are
, if there are
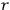 but not
but not
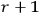 independent integer relations among them, that is, if
there is a set of
independent integer relations among them, that is, if
there is a set of
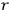 mutually independent
mutually independent
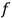 -tuples
-tuples
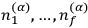 ,
,
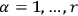 of integers, so that
of integers, so that
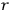 relations of the form
relations of the form
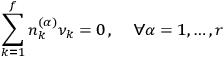
|
8.11 |
hold, but there are not
 relations of this sort.
The
relations of this sort.
The
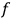 -tuple is simply called degenerate if it is
-tuple is simply called degenerate if it is
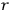 -fold
degenerate for some
-fold
degenerate for some
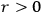 . A relation of the form
(8.11) is called a commensurability. If no
commensurabilities exist, the system is called non-degenerate
or incommensurable.
. A relation of the form
(8.11) is called a commensurability. If no
commensurabilities exist, the system is called non-degenerate
or incommensurable.
It is clear that a relation of the form (8.11)
with
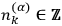 exists if and only if it
exists for
exists if and only if it
exists for
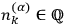 (rational numbers).
Hence a more compact definition of
(rational numbers).
Hence a more compact definition of
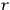 -fold degeneracy is
the following: Consider the real numbers
-fold degeneracy is
the following: Consider the real numbers
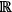 as a vector space over the rational numbers
as a vector space over the rational numbers
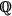 (which is infinite dimensional). The
(which is infinite dimensional). The
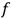 vectors
vectors
 are
are
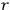 -fold degenerate if and only if their span is
-fold degenerate if and only if their span is
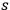 -dimensional, where
-dimensional, where
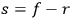 .
.
Strictly speaking, we have to distinguish between proper
(eigentlich, Born) and improper (or contingent)
(zufällig, Born) degeneracies. To understand the
difference, recall that the
frequencies are defined through (8.10),
so that each of them is a function of the action variables
 . A proper degeneracy holds identically for all
considered values,
. A proper degeneracy holds identically for all
considered values,
 , (the set of which must contain at least an open interval of values around each considered value,
, (the set of which must contain at least an open interval of values around each considered value,
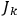 ), whereas an improper degeneracy only holds for singular
values of the
), whereas an improper degeneracy only holds for singular
values of the
 ’s. This distinction should then also be made
for the notion of
’s. This distinction should then also be made
for the notion of
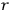 -fold degeneracy: a proper
-fold degeneracy: a proper
 -fold
degeneracy of frequencies is one that holds identically for
a whole neighborhood of values
-fold
degeneracy of frequencies is one that holds identically for
a whole neighborhood of values
 around the
considered value.
around the
considered value.
The possibility of degeneracies and their relevance for the
formulation of quantization conditions was already anticipated
by  vanished, say
vanished, say
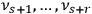 where
where
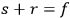 , then no quantum condition should be
imposed on the corresponding actions
, then no quantum condition should be
imposed on the corresponding actions
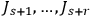 .
The rationale he gave for that description was that defining
equation (8.10) for the frequencies showed
that the energy
.
The rationale he gave for that description was that defining
equation (8.10) for the frequencies showed
that the energy
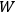 was independent of
was independent of
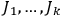 .
In his words (but our notation):
.
In his words (but our notation):
This amendment to the prescription [of quantization] is suggested by the remark, that for a vanishing mean motion, the equation
shows that the energy becomes independent of the variables
, that therefore these variables have no relation to the energetic process within the system. (Schwarzschild 1916, 550)
From that it is clear that the independence of the energy
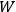 from
the
from
the
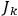 for which
for which
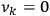 is only given if the system is
properly degenerate; otherwise we just have a stationary
point in
is only given if the system is
properly degenerate; otherwise we just have a stationary
point in
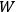 with respect to
with respect to
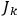 at one particular
at one particular
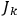 value.
So
value.
So  (for some open neighborhood).
(for some open neighborhood).
Now, it is true that for a
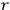 -fold degenerate system (proper
or improper) a canonical transformation exists such that, say,
the first
-fold degenerate system (proper
or improper) a canonical transformation exists such that, say,
the first
 frequencies
frequencies
 are
non-degenerate, whereas the remaining
are
non-degenerate, whereas the remaining
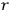 frequencies
frequencies

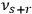 are all zero (only for the
particular values of
are all zero (only for the
particular values of
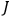 ’s in the improper case). The number
’s in the improper case). The number
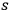 of independent frequencies is called the degree of periodicity
of the system (Born 1925, 105).
Hence
of independent frequencies is called the degree of periodicity
of the system (Born 1925, 105).
Hence 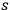 action variables
action variables
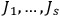 should be quantized, but not the remaining
should be quantized, but not the remaining
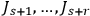 . If the degeneracies are improper,
similar systems with arbitrarily close values of the
. If the degeneracies are improper,
similar systems with arbitrarily close values of the
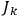 would have these variables
quantized, so that it would seem physically unreasonable to treat
such singular cases differently, as
would have these variables
quantized, so that it would seem physically unreasonable to treat
such singular cases differently, as
Born now proceeds to generalize the uniqueness theorem to degenerate
systems. For this, one needs to find the most general
transformations that preserve conditions A-C and, in addition, preserve
the separation into
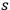 independent and
independent and
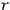 mutually
dependent (vanishing) frequencies. This can indeed be done,
so that the above theorem has the following natural
generalization:
mutually
dependent (vanishing) frequencies. This can indeed be done,
so that the above theorem has the following natural
generalization:
Theorem (Uniqueness for degenerate systems) If, for a mechanical system, variablescan be introduced satisfying conditions A-C, then they can always be chosen in such a way that the first
of the partial derivatives
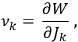
|
8.12 |
i.e. theare incommensurable and the others
, where
, vanish. Then the first
action variables,
, are determined uniquely up to transformations of type (8.6a) [that is, linear transformations by
]. (Born 1925, 108)
In the next section (§ 16), Born completes these results
by showing that adiabatic invariance holds for
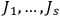 but not for
but not for
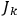 for
for
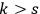 , even if the degeneracy is merely
improper (Born 1925, 111).
He therefore arrives at the following
, even if the degeneracy is merely
improper (Born 1925, 111).
He therefore arrives at the following
Quantization rule: Let the variablesfor a mechanical system satisfying conditions A-C be so chosen that
are incommensurable and
(
) vanish (possibly
). The stationary motions of this systems are then determined by
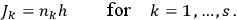
|
8.13 |
Born acknowledges that
8.4.1 A Simple System with (Proper) Degeneracies
To illustrate the occurrence of degeneracies, we present, in a slightly abbreviated form, the example of the 3-dimensional harmonic oscillator, which Born discusses in § 14 for the same purpose. Its Hamiltonian reads
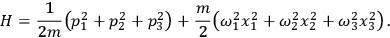
|
8.14 |
The general solution to the 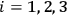 ):
):
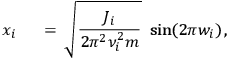
|
8.15a |
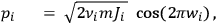
|
8.15b |
where
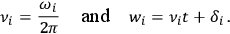
|
8.15c |
The
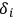 and
and
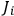 are six integration constants, in terms
of which the total energy reads
are six integration constants, in terms
of which the total energy reads
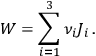
|
8.16 |
Now, a one-fold degeneracy occurs if the frequencies
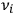 obey
a single relation of the form
obey
a single relation of the form
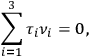
|
8.17 |
where
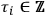 . This happens, for example, if
. This happens, for example, if
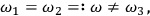
|
8.18 |
in which case the Hamiltonian is invariant under rotations around the third axis. The energy then only depends on
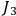 and the sum
and the sum
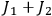 . Introducing coordinates
. Introducing coordinates
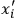 with respect to a system of axes that are rotated by an angle
with respect to a system of axes that are rotated by an angle
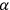 around the third axis,
around the third axis,
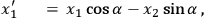
|
8.19a |
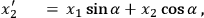
|
8.19b |
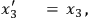
|
8.19c |
under which transformation the momenta transform just like the coordinates.14
The new action variables,
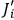 , are given in terms of the old
, are given in terms of the old
 by:
by:
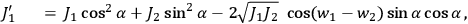
|
8.20a |
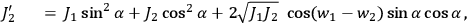
|
8.20b |

|
8.20c |
As Born stresses, the
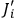 ’s depend not only on the
’s depend not only on the
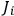 ’s, but also
on the
’s, but also
on the
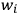 ’s, more precisely on the difference
’s, more precisely on the difference
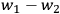 , which
is a constant, (
, which
is a constant, (
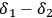 ), along the dynamical trajectory
according to (8.15c) and (8.18),
as it must be (since the
), along the dynamical trajectory
according to (8.15c) and (8.18),
as it must be (since the
 ’s are constant). It is now clear that,
for general
’s are constant). It is now clear that,
for general
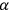 , the conditions
, the conditions
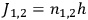 and
and
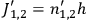 are mutually incompatible.
However, (8.20) show that the sums
are invariant
are mutually incompatible.
However, (8.20) show that the sums
are invariant
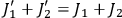
|
8.21 |
hence a condition for the sum
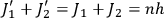
|
8.22a |
together with

|
8.22b |
makes sense.
But what about coordinate changes other than just rotations?
To see what happens, Born considers instead of
(8.19) the transformation to cylindrical
polar coordinates
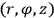 with conjugate momenta
with conjugate momenta
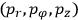 (cf. footnote 14):
(cf. footnote 14):
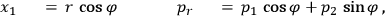
|
8.23a |

|
8.23b |

|
8.23c |
The transformation equations from the old
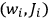 to the new
action variables
to the new
action variables
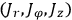 are:15
are:15

|
8.24a |

|
8.24b |
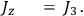
|
8.24c |
The total energy expressed as a function of the new action variables reads:
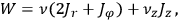
|
8.25 |
where here and in (8.24)
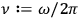 and
and
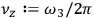 (cf. 8.18).
Again it is only the combination
(cf. 8.18).
Again it is only the combination
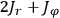 that enters the energy
expression, and from (8.24) we see immediately
that
that enters the energy
expression, and from (8.24) we see immediately
that

|
8.26 |
Again, conditions of the form
 ,
,
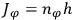 , and
, and
 would pick out different “quantum orbits”
[Quantenbahnen, Born] than those corresponding
to
would pick out different “quantum orbits”
[Quantenbahnen, Born] than those corresponding
to
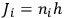 . The energies, however, are the same.
. The energies, however, are the same.
8.5 Einstein’s View
By 1917
In this paper Einstein suggested replacing the quantum condition (8.2) with
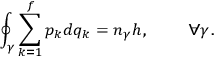
|
8.27 |
First of all one should recognize that here the sum forms the integrand, rather
than each individual term
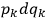 as in
(8.2).
Second, (8.27) is not just one but
many conditions, as many as there are independent paths
(loops)
as in
(8.2).
Second, (8.27) is not just one but
many conditions, as many as there are independent paths
(loops)
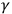 along which the integrand is integrated.
along which the integrand is integrated.
Let us explain the meaning of all this in a modernized terminology. For this, we first point out that the integrand has a proper geometric meaning, since
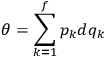
|
8.28 |
is the coordinate expression of a global one-form on
phase space (sometimes called the Liouville form),17 quite in
contrast to each individual term
 , which have no
coordinate-independent, geometric meaning. Being a one-form
it makes unambiguous sense to integrate it along paths.
The paths
, which have no
coordinate-independent, geometric meaning. Being a one-form
it makes unambiguous sense to integrate it along paths.
The paths
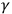 considered here are all closed, i.e. loops,
hence the
considered here are all closed, i.e. loops,
hence the
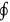 -sign. But what are the loops
-sign. But what are the loops
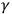 that may enter (8.27)? For their
characterisation it is crucial to assume that the system
be integrable. This means that there are
that may enter (8.27)? For their
characterisation it is crucial to assume that the system
be integrable. This means that there are
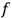 (
(
 number
of degrees of freedom) functions on phase space,
number
of degrees of freedom) functions on phase space,
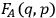 (
(
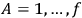 ), the energy being one of them, whose
mutual Poisson brackets vanish:
), the energy being one of them, whose
mutual Poisson brackets vanish:
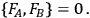
|
8.29 |
This implies that the trajectories remain on the level sets for the
 -component function
-component function
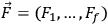 , which can be shown to be
, which can be shown to be
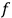 -dimensional tori
-dimensional tori
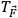 embedded in
embedded in
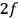 -dimensional phase space. From (8.29) it follows that these tori are geometrically special (Lagrangian) submanifolds: The differential of the one form (8.27), restricted to the tangent spaces of these tori, vanishes identically. By Stokes’s theorem this implies that any two integrals of
-dimensional phase space. From (8.29) it follows that these tori are geometrically special (Lagrangian) submanifolds: The differential of the one form (8.27), restricted to the tangent spaces of these tori, vanishes identically. By Stokes’s theorem this implies that any two integrals of
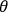 over loops
over loops
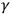 and
and
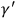 within the same torus
within the same torus
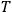 coincide in value (possibly up to a sign, depending on the orientation given to the loops) if there is a 2-dimensional surface
coincide in value (possibly up to a sign, depending on the orientation given to the loops) if there is a 2-dimensional surface
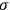 within
within
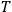 whose boundary is just the union of
whose boundary is just the union of
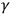 and
and
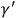 . This defines an equivalence relation on the set of loops on
. This defines an equivalence relation on the set of loops on
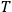 whose equivalence classes are called homology classes (of dimension 1). The homology classes form a finitely generated Abelian group (since the level sets are compact) so that each member can be uniquely written as a linear combination of
whose equivalence classes are called homology classes (of dimension 1). The homology classes form a finitely generated Abelian group (since the level sets are compact) so that each member can be uniquely written as a linear combination of
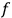 basis loops (i.e. their classes) with integer coefficients. For example, if one pictures the
basis loops (i.e. their classes) with integer coefficients. For example, if one pictures the
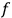 -torus as an
-torus as an
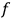 -dimensional cube with pairwise identifications of opposite faces through translations, an
-dimensional cube with pairwise identifications of opposite faces through translations, an
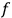 -tuple of basis loops is represented by the straight lines-segments connecting the midpoints of opposite faces. Each such basis is connected to any other by a linear
-tuple of basis loops is represented by the straight lines-segments connecting the midpoints of opposite faces. Each such basis is connected to any other by a linear
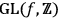 transformation.
transformation.
Now we can understand how (8.27) should be read, namely as a condition that selects, out of a continuum, a discrete subset of tori
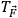 , which may be characterized by discretized values for the
, which may be characterized by discretized values for the
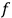 observables
observables
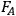 . In light of the last remark of the previous paragraph, it does not matter which basis for the homology classes of loops one chooses to evaluate (8.27). This leads to a quantization condition independent of the need to separate variables.
. In light of the last remark of the previous paragraph, it does not matter which basis for the homology classes of loops one chooses to evaluate (8.27). This leads to a quantization condition independent of the need to separate variables.
What remains undecided at this stage is how to proceed in cases where degeneracies occur. In the absence of degeneracies, the torus is uniquely determined. It is the closure of the phase space trajectory for all times. If degeneracies exist, that closure will define a torus of dimension
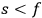 , the embedding of which in a torus of dimension
, the embedding of which in a torus of dimension
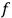 is ambiguous since the latter is not uniquely determined by the motion of the system. This we have seen in Born’s examples above. Even simpler examples would be the planar harmonic oscillator and planar Keplerian motion (cf. Arnold 1978, sec. 51). In such cases one has to decide whether (8.27) is meant to apply only to the
is ambiguous since the latter is not uniquely determined by the motion of the system. This we have seen in Born’s examples above. Even simpler examples would be the planar harmonic oscillator and planar Keplerian motion (cf. Arnold 1978, sec. 51). In such cases one has to decide whether (8.27) is meant to apply only to the
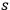 generating loops of the former, lower-dimensional torus or to all
generating loops of the former, lower-dimensional torus or to all
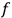 of the latter, thus introducing an
of the latter, thus introducing an
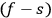 -fold ambiguity in the determination of the “quantum orbits” [Quantenbahnen, Born].
-fold ambiguity in the determination of the “quantum orbits” [Quantenbahnen, Born].
The geometric flavor of these arguments is clearly present in 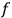 -dimensional configuration space whose coordinates are defined by the
-dimensional configuration space whose coordinates are defined by the
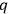 ’s and regards the
’s and regards the
 ’s as certain ‘functions’ on it, defined through an
’s as certain ‘functions’ on it, defined through an
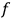 -parameter family of solutions. Locally in
-parameter family of solutions. Locally in
 -space (i.e. in a neighborhood or each point)
-space (i.e. in a neighborhood or each point) 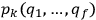 . However, following a dynamical trajectory that is dense in a portion of
. However, following a dynamical trajectory that is dense in a portion of
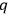 -space the values
-space the values
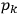 need not return to their original values. Einstein distinguishes between two cases: either the number of mutually different
need not return to their original values. Einstein distinguishes between two cases: either the number of mutually different
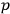 -values when the trajectory returns to within a small neighborhood
-values when the trajectory returns to within a small neighborhood
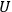 around a point in
around a point in
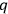 -space is finite, or it is infinite. In the latter case, Einstein’s quantization condition does not apply. In the former case, Einstein’s considers what he, in the letter to
-space is finite, or it is infinite. In the latter case, Einstein’s quantization condition does not apply. In the former case, Einstein’s considers what he, in the letter to 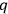 -space, that is, a finite-sheeted covering. The components
-space, that is, a finite-sheeted covering. The components
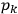 will then be a well-defined (single-valued) co-vector field over the dynamically allowed portion of
will then be a well-defined (single-valued) co-vector field over the dynamically allowed portion of
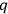 -space (see (Stone 2005) for a lucid discussion with pictures).
-space (see (Stone 2005) for a lucid discussion with pictures).
In a most interesting, one and a half page supplement added as proof, Einstein points out that the first type of motion, where
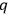 -space trajectories return with infinitely many mutually different
-space trajectories return with infinitely many mutually different
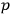 -values, may well occur for simple systems with relatively few degrees of freedom, e.g. that of three point-like masses moving under the influence of their mutual gravitational attractions, as was first pointed out by
-values, may well occur for simple systems with relatively few degrees of freedom, e.g. that of three point-like masses moving under the influence of their mutual gravitational attractions, as was first pointed out by
Hence one arrives at the conclusion that the crucial question concerning the applicability of quantization conditions is that of integrability, i.e. whether sufficiently many constants of motion exist; other degrees of complexity, like the number of degrees of freedom, do not directly matter. As we know from Poincaré’s work, non-integrability occurs already at the 3-body level for simple 2-body interactions. But what is the meaning of “Quantum Theory” if “quantization” is not a universally applicable procedure?18
In the letter to
As pretty as this may appear, it is just restricted to the special case where thecan be represented as (multi-valued) functions of the
. It is interesting that this restriction just nullifies the validity of statistical mechanics. The latter presupposes that upon recurrence of the
, the
of a system in isolation assume all values by and by which are compatible with the energy principle. It seems to me, that the true [wirkliche] mechanics is such that the existence of the integrals (which exclude the validity of statistical mechanics) is already assured by the general foundations. But how to start??19 (Kormos Buchwald 1987–2005, Vol. 8, Part A, Doc. 350, 465, my emphasis)
Did we just witness
8.6 Final Comments
In his book, Born also mentions 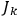 ’s and hence impossible to pose quantization rules in general. His conclusion from this is that, for the time being,
one should adopt a pragmatic attitude:
’s and hence impossible to pose quantization rules in general. His conclusion from this is that, for the time being,
one should adopt a pragmatic attitude:
Even though the mentioned approximation scheme does not converge in the strict sense, it has proved useful in celestial mechanics. For it could be shown [by Poincaré] that the series showed a type of semi-convergence. If appropriately terminated they represent the motion of the perturbed system with great accuracy, not for arbitrarily long times, but still for practically very long times. From this one sees on purely theoretical grounds, that the absolute stability of atoms cannot be accounted for in this way. However, for the time being one will push aside [sich hinwegsetzen] this fundamental difficulty and make energy calculations test-wise, in order to see whether one obtains similar agreements as in celestial mechanics. (Born 1925, 292–293)
Ten pages before that passage, in the introduction to the chapter on perturbation theory, Born stressed the somewhat ambivalent situation perturbation theory in atomic physics faces in comparison to celestial mechanics: On one hand, ‘perturbations’ caused by electron-electron interactions are of the same order of magnitude than electron-nucleus interactions, quite in contrast to the solar system, where the sun is orders of magnitude heavier than the planets. On the other hand, the quantum conditions drastically constrain possible motions and could well act as regulator. As regards the analytical difficulties already mentioned above, he comments in anticipation:
Here [convergence of Fourier series] an insurmountable analytical difficulty seems to inhibit progress, and one could arrive at the opinion that it is impossible to gain a theoretical understanding of atomic structures up to Uranium. (Born 1925, 282–283)
However,
The aim of the investigations of this chapter shall be to demonstrate, that this difficulty is not essential. It would indeed be strange [sonderbar] if Nature barricaded herself behind the analytical difficulties of the-body problem against the advancement of knowledge [das Vordringen der Erkenntnis]. (Born 1925, 282–283)
In the course of the development of his chapter on perturbation theory very interesting technical points come up, one of them being connected with the apparent necessity to impose quantization conditions for the unperturbed action variables conjugate to angles whose frequencies are improperly degenerate. But the discussion of this is quite technical and extraneous to Born’s approach to the quantization procedure.
References
Abraham, Ralph, Jerrold E. Marsden (1978). Foundations of Mechanics. Reading, MA: Benjamin/Cummings Publishing Company.
Arnold, Vladimir Igorevich (1978). Mathematical Methods of Classical Mechanics. New York: Springer.
Born, Max (1925). Vorlesungen über Atommechanik. Erster Band. Volume II of . Berlin: Julius Springer.
Born, Max, Pascual Jordan (1930). Elementare Quantenmechanik (zweiter Band der Vorlesungen über Atommechanik). Volume IX of . Berlin: Julius Springer.
Burgers, Johannes Martinus (1918) Het atoommodel van Rutherford-Bohr. phdthesis. University of Leyden
Charlier, Carl Ludwig (1902). Die Mechanik des Himmels. Leipzig: Veit.
- (1907). Die Mechanik des Himmels. Leipzig: Veit.
de Broglie, Louis (1925). Recherches sur la théorie des quanta. Annales de Physique 3(10 Série): 22-128
- (1929). Einführung in die Wellenmechanik. Leipzig: Akademische Verlagsgesellschaft.
Epstein, Paul S. (1916a). Zur Theorie des Starkeffektes. Annalen der Physik 355(13): 489-520
- (1916b). Zur Quantentheorie. Annalen der Physik 356(18): 168-188
Frenkel, Jakov (1929). Einführung in die Wellenmechanik. Berlin: Julius Springer.
Goldstein, Herbert, Charles P. Poole Jr, C.P. P. (2001). Classical Mechanics. Reading, MA: Addison-Wesley.
Green, Herbert S., Max Born (1965). Matrix Mechanics. Groningen: P. Noordhoff Ltd. Scientific Publications.
Gutzwiller, Martin C. (1990). Chaos in Classical and Quantum Mechanics. New York: Springer.
Haas, Arthur (1928). Materiewellen und Quantenmechanik. Leipzig: Akademische Verlagsgesellschaft.
Heisenberg, Werner (1925). Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen. Zeitschrift für Physik 33(1): 879-893
- (1967). Einführung in die einheitliche Feldtheorie der Elementarteilchen. Stuttgart: S. Hirzel.
Hermann, Armin (1968). Albert Einstein/Arnold Sommerfeld Briefwechsel. Sechzig Briefe aus dem goldenen Zeitalter der modernen Physik. Basel: Schwabe & Co..
Ishiwara, Jun (1915). Die universelle Bedeutung des Wirkungsquantums. Toyko Sugaku Buturigakkawi Kizi (Proceedings of the Tokyo Mathematical and Physical Society) 8(5): 106-116
Keller, Joseph B. (1958). Corrected Bohr-Sommerfeld Quantum Conditions for Nonseparable Systems. Annals of Physics 4(2): 180-188
Kormos Buchwald, Diana et al. (1987–2005). The Collected Papers of Albert Einstein. Princeton: Princeton University Press.
Kronig, Ralph, Victor F. Weisskopf (1964). Collected Scientific Papers by Wolfgang Pauli. New York: Interscience Publishers.
Pauli, Wolfgang (1925). Review of Max Born: Vorlesungen über Atommechanik. Erster Band. Die Naturwissenschaften 13: 487-488
- (1930). Review of Max Born & Pascual Jordan: Elementare Quantenmechanik. Zweiter Band der Vorlesungen über Atommechanik. Die Naturwissenschaften 18: 602
Planck, Max (1916). Die physikalische Struktur des Phasenraumes. Annalen der Physik 355(12): 385-418
Schwarzschild, Karl (1916). Zur Quantenhypothese. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin
Seth, Suman (2010). Crafting the Quantum. Arnold Sommerfeld and the Practice of Theory, 1890–1926. Cambridge, MA: The MIT Press.
Sommerfeld, Arnold (1916). Zur Quantentheorie der Spektrallinien. Annalen der Physik 356(17): 1-94
- (1929). Atombau und Spektrallinien. Wellenmechanischer Ergänzungsband. Braunschweig: Friedrich Vieweg und Sohn.
- (1977). Vorlesungen über theoretische Physik. Band 1 Mechanik. Thun: Harri Deutsch.
Stone, Douglas A. (2005). Einstein's Unknown Insight and the Problem of Quantizing Chaos. Physics Today 58(8): 37-43
Wilson, William (1915). The Quantum-Theory of Radiation and Line Spectra. Philosophical Magazine 6th Series 29(174): 795-802
Footnotes
As usual, I use the term “Bohr-Sommerfeld quantization” throughout as shorthand for what probably should be called Bohr-Ishiwara-Wilson-Planck-Sommerfeld-Epstein-Schwarzschild … quantization.
Born and Jordan mention the following four books: Arthur Haas’s Materiewellen und Quantenmechanik (1928), Arnold Sommerfeld’s Atombau und Spektrallinien, Vol. 2 (Wellenmechanischer Ergänzungsband) (1929), Louis de Broglie’s Einführung in die Wellenmechanik (1929), and Yakov Frenkel’s Einführung in die Wellenmechanik (1929).
The preface is dated November 1924.
A partial revival and refinement of Bohr-Sommerfeld quantization occurred during the late 1950s, as a tool to construct approximate solutions to Schrödinger’s equation, even for non-separable systems (Keller 1958); see also (Gutzwiller 1990). Ever since it has remained an active field of research in atomic and molecular physics.
In the latest editions (2001 English, 2006 German) (Goldstein et.al. 2001) the authors seem to have erased all references to Born’s book.
Translations are the author’s unless otherwise noted.
Here Born adds the following footnote: “Measurements of atomic radii and the like do not lead to better approximations to reality [Wirklichkeit] as, say, the coincidence between orbital and light frequencies.”
The implication of integrability for separability is far less clear (compare, e.g., Gutzwiller 1990). Classic results concerning sufficient conditions for separability were obtained by Stäckel (see Charlier 1902).
Note that the inverse matrices must also be
integer-valued; hence the matrices must have determinant equal
to
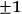 .
.
We follow Born’s notation, according to which
the Hamiltonian, considered as function of the action
variables, is denoted by
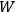 .
.
Generally, the momenta, being elements of the vector space dual to the velocities, transform via the inverse-transposed of the Jacobian (differential) for the coordinate transformation. But for linear transformations the Jacobian is just the transformation matrix and it being an orthogonal matrix implies that its inverse equals its transpose.
Einstein’s paper was cited by de Broglie in his thesis (de Broglie 1925), where he spends slightly more than a page (pages 64–65 of Section II in Chapter III) discussing the “interpretation of Einstein’s quantisation condition,” and also in Schrödinger’s “Quantisation as Eigenvalue Problem”, where in the Second Communication he states in a footnote that Einstein’s quantization condition “amongst all older versions stands closest to the present one [Schrödinger’s].” However, after matrix and wave mechanics settled, Einstein’s paper seems to have been largely forgotten until Keller (1958) reminded the community of its existence.
In the terminology of differential geometry, phase
space is the cotangent bundle
 over configuration space
over configuration space
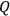 with projection map
with projection map
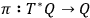 . The one-form
. The one-form
 on
on
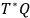 is defined by the following rule:
Let
is defined by the following rule:
Let
 be a point in
be a point in
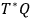 and
and
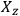 a vector in the
tangent space of
a vector in the
tangent space of
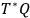 at
at
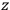 , then
, then
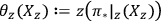 .
Here the symbol on the right denotes the differential of
the projection map
.
Here the symbol on the right denotes the differential of
the projection map
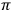 , evaluated at
, evaluated at
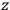 and then applied
to
and then applied
to
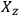 . This results in a tangent vector at
. This results in a tangent vector at
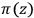 on
on
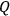 on which
on which
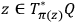 may be evaluated. In local
adapted coordinates
may be evaluated. In local
adapted coordinates
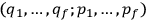 the projection map
the projection map
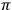 just projects onto the
just projects onto the
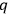 s.
Then, for
s.
Then, for
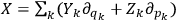 we have
we have
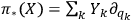 and
and
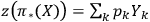 , so that
, so that
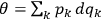 .
.
Even today this question has not yet received a unanimously accepted answer.
So hübsch nun diese Sache ist, so ist sie eben auf den Spezialfall beschränkt, dass die
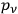 als (mehrdeutige) Funktion der
als (mehrdeutige) Funktion der
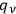 dargestellt werden können. Es ist interesstant, dass diese Beschränkung gerade die Gültigkeit der statistischen Mechanik aufhebt. Denn diese setzt voraus, dass die
dargestellt werden können. Es ist interesstant, dass diese Beschränkung gerade die Gültigkeit der statistischen Mechanik aufhebt. Denn diese setzt voraus, dass die
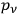 eines sich selbst überlassenen Systems bei Wiederkehr der
eines sich selbst überlassenen Systems bei Wiederkehr der
 nach und nach alle mit dem Energieprinzip vereinbaren Wertsysteme annehmen. Es scheint mir, dass die wirkliche Mechanik so ist, dass die Existenz der Integrale, (welche die Gültigkeit der statistischen Mechanik ausschliessen), schon vermöge der allgemeinen Grundlagen gesichert ist. Aber wie ansetzen??
nach und nach alle mit dem Energieprinzip vereinbaren Wertsysteme annehmen. Es scheint mir, dass die wirkliche Mechanik so ist, dass die Existenz der Integrale, (welche die Gültigkeit der statistischen Mechanik ausschliessen), schon vermöge der allgemeinen Grundlagen gesichert ist. Aber wie ansetzen??




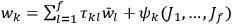 ,
into which our equation turns if we redefine the
functions through
,
into which our equation turns if we redefine the
functions through
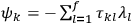 .
.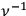 in his formula (21) in § 14 of Chapter 2. My formulae correct Born’s formulae on his p. 98.
in his formula (21) in § 14 of Chapter 2. My formulae correct Born’s formulae on his p. 98.