The problems presented in Chapters 2–5 were so different one from the others that it was necessary to accompany each of them with a copious commentary. In order to allow the reader who may like to explore some Old Babylonian texts without being held firmly by the hand, this appendix contains problems in translation only, or at most accompanied by the most necessary clarifications. Some are counterparts of problems that were presented above and come from the same tablets.
TMS XVI #2
13The 4th of the width to that by which the length goes beyond the width, to join,
1415′. You, 15′ to 4 raise, 1 you see, what is it?
154 and 1 posit.
1615′ scatter. 10′, the going-beyond, and 5′, the joined, posit. 20′, the width,
17to 10′, the going-beyond, join, 30′ the length, and 20′, to tear out, posit. 5′ to 4 raise,
1820′ you see. 20′, the width, to 4 raise, 1°20′ you see.
1930′, the length, to 4 raise, 2 you see. 20′, the width,
20from 1°20′ tear out, 1 you see. 1
21from 2, the lengths, tear out, 1 you see, what is it?
22From 4, of the fourth, 1 tear out, 3 you see. igi 4 detach, 15′ you see.
2315′ to 3 raise, 45′ you see, as as much as (there is) of widths posit. Posit to tear out.
241 as as much as (there is) of lengths posit. [...] 1 take, to 1 length
25raise, 30′ you see. 20′ the width, 20′ to 45′, (as much as (there is) of) widths, raise,
2615′ you see, 15′ to 15′ join, 30′ you see, 30 the length.
Commentary: see #1 of the same tablet, page
TMS VII #1
1The 4th of the width to the length I have joined, its 7
 th
th
 to 10 I have gone,
to 10 I have gone,
2as much as the heap of length and
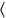 width
width
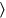 . You, 4 posit; 7 posit;
. You, 4 posit; 7 posit;
310 posit; 5′ to 7 raise, 35′ you see.
430′ and 5′ single out. 5′, the step, to 10 raise,
550′ you see. 30′ and 20′, posit. 5′, the step, to 4, of the fourth of the width,
6raise: 20′ you see, 20′, the width. 30′ to 4, of the fourth,
7raise, 2 you see. 2 posit, lengths. 20′ from 20′ tear out,
8and from 2, 30′ tear out, 1°30′ you see.
9From 4, of the fourth, 1 tear out, 3 {…} you see.
10igi 3 detach, 20′ you see. 20′ to 1°30′ raise:
1130′ you see, 30′ the length. 30′ from 50′ tear out, 20′ you see, 20′ the width.
12Turn back. 7 to 4, of the fourth, raise, 28 you see.
1310 from 28 tear out, 18 you see. igi 3 detach,
1420′ you see. 20′ to 18 raise, 6 you see, 6 (for) the length.
156 from 10 tear out, 4 (for) the width. 5′ to 6 raise,
1630′ the length. 5′ to 4 raise, 20′ you see, 20′ the
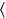 width
width
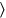 .
.
Commentary: see #2 of the same tablet, page
VAT 8389 #1
Obv. I
1From 1 bùr 4 gur of grain I have collected,
2from 1 second bùr 3 gur of grain I have collected.
3grain over grain, 8‵20 it went beyond
4My plots I have accumulated: 30‵.
5My plots what?
630‵, the bùr, posit. 20‵, the grain which he has collected, posit.
730‵, the second bùr, posit.
815‵, the grain which he has collected,
98‵20 which the grain over the grain went beyond,
10and 30‵ the accumulation of the surfaces of the plots posit:
1130‵ the accumulation of the surfaces of the plots
12to two break: 15‵.
1315‵ and 15‵ until twice posit:
14igi 30‵, of the bùr, detach:
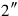 .
.
15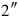 to 20‵, the grain which he has collected,
to 20‵, the grain which he has collected,
16raise, 40′ the false grain; to 15‵ which until twice
17you have posited,
18raise, 10‵ may your head hold!
19igi 30, of the second bùr, detach,
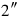 .
.
20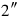 to 15‵, the grain
to 15‵, the grain
21raise, 30′ the false grain; to 15 which until twice
22you have posited, raise, 7‵30.
2310‵ which your head holds
24over 7‵30 what goes beyond? 2‵30 it goes beyond.
252‵30 which it goes beyond, from 8‵20
26which the grain over the grain goes beyond,
Obv. II
1tear out: 5‵50 you leave.
25‵50 which you have left
3may your head hold!
440′, the change, and 30′, the change,
5accumulate: 1°10′. The igi I do not know.
6What to 1°10′ may I posit
7which 5‵50 which your head holds gives me?
85‵ posit. 5‵ to 1°10 raise.
95‵50 it gives to you.
105‵ which you have posited, from 15‵ which until twice
11you have posited, from one tear out,
12to one join:
13The first is 20‵, the second is 10‵.
1420‵ (is) the surface of the first plot, 10‵ (is) the surface of the second plot.
15If 20‵ (is) the surface of the first plot,
1610‵ the surface of the second plot, their grains what?
17igi 30‵, of the bùr, detach:
 .
.
18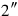 to 20‵, the grain which he has collected,
to 20‵, the grain which he has collected,
19raise, 40′. To 20‵, the surface of the first plot,
20raise, 13‵20 the grain of 20‵, the surface of the plot.
21igi 30‵, of the second bùr, detach:
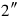 .
.
22 to 15‵, the grain which he has collected, raise, 30′.
to 15‵, the grain which he has collected, raise, 30′.
2330′ to 10‵, the surface of the second plot
24raise, 5 the grain of the surface of the second plot.
2513‵30 the grain of ¿the surface? of the first plot
26over 5 the grain of ¿the surface? of the second plot
27what goes beyond? 8‵20 it goes beyond.
This problem belongs to one of two twin tablets, containing a total of ten problems about the rent paid for two parcels of a field. On one parcel the rent is 4 gur
As explained on page
A modern reader may find it strange that the two rents per bùr, which in lines I.1–2 are given in gur (per bùr), are translated into sìla in lines I.6–7 without multiplication; in general, as we see, the text skips no intermediate step. The explanation is that the conversion is made by means of a “metrological table”
The modern reader may also wonder that the text does not indicate once for all the value of the bùr in sìla and its igi. Once more the reason is that the text describes the Old Babylonian calculational technique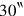 sar per bùr) and 2 (
sar per bùr) and 2 (
 , igi 30‵)—and afterwards, by means of the multiplication
, igi 30‵)—and afterwards, by means of the multiplication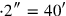 sìla per sar).
sìla per sar).
A small explanation may be necessary in order to facilitate understanding of the procedure: first the text determines what the difference between the two rents would be if the two parcels had been equal in area, that is, 15‵ sar each. This difference is not large enough—it is 2‵30 sìla, 5‵50 sìla too small—and therefore the first parcel must be enlarged. Each time a sar is transferred from the second to the first parcel, the difference grows by 40′+30′ sìla (the two “changes”
At the end we find a numerical verification
VAT 8390 #1
Obv. I
1Length and width I have made hold: 10‵ the surface.
2The length to itself I have made hold:
3a surface I have built.
4So much as the length over the width went beyond
5I have made hold, to 9 I have repeated:
6as much as that surface which the length by itself
7was made hold.
8The length and the width what?
910‵ the surface posit,
10and 9 (to) which he has repeated posit:
11The equalside of 9 (to) which he has repeated what? 3.
123 to the length posit
133 to the width posit.
14Since “so much as the length over the width went beyond
15I have made hold,” he has said
161 from 3 which to the width you have posited
17tear out: 2 you leave.
182 which you have left to the width posit.
193 which to the length you have posited
20to 2 which
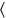 to
to
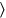 the width you have posited raise, 6.
the width you have posited raise, 6.
21igi 6 detach: 10′.
2210′ to 10‵ the surface
23The equalside of 1‵40 what? 10.
Obv. II
110 to 3 which to the length you have posited
2raise, 30 the length.
310 to 2 which to the width you have posited
4raise, 20 the width.
5If 30 the length, 20 the width,
6the surface what?
730 the length to 20 the width raise, 10‵ the surface.
830 the length together with 30 make hold: 15‵.
930 the length over 20 the width what goes beyond? 10 it goes beyond.
1010 together with 10 make hold: 1‵40.
111‵40 to 9 repeat: 15‵ the surface.
1215‵ the surface, as much as 15‵ the surface which the length
13by itself was made hold.
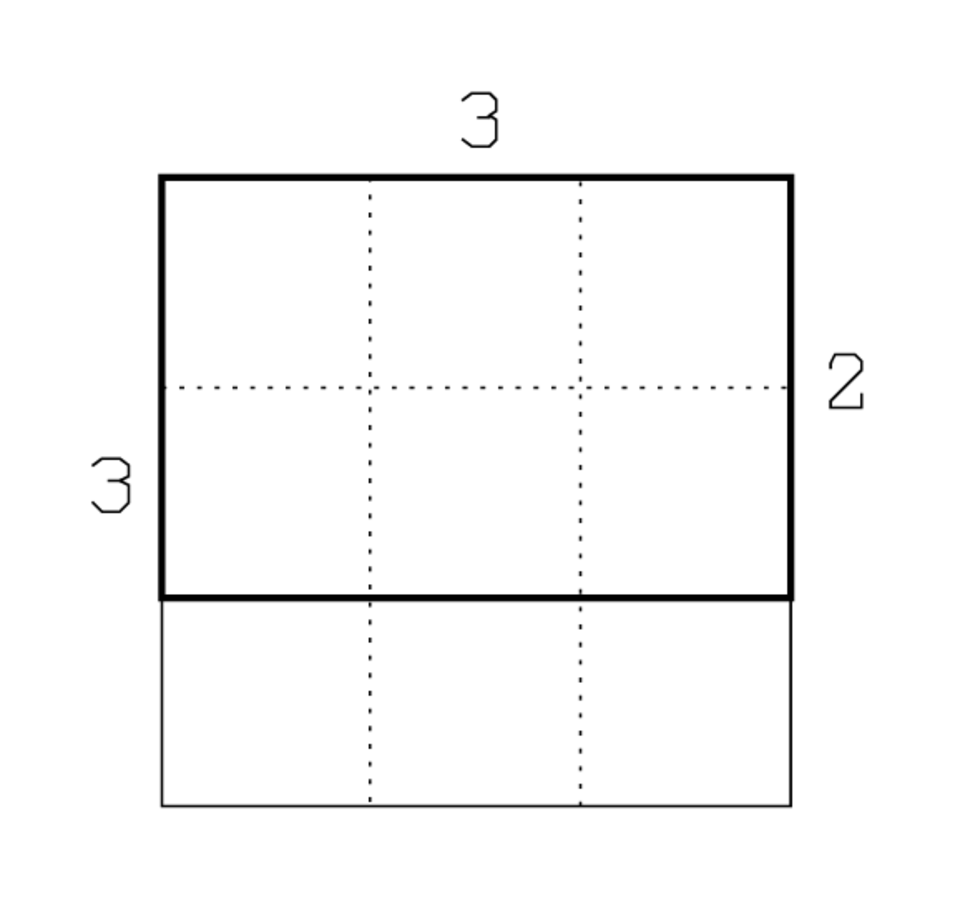
As support for the interpretation, a diagram may serve (Figure 1). Then the text almost explains itself, in particular if one keeps in mind BM 13901 #10
One should take note of the use of the multiplicative operations “make hold,” “raise”
VAT 8520 #1
Obv.
1The 13th from the heap of the igûm and the igibûm
2to 6 I have repeated, from the inside of the igûm
3I have torn out: 30′ I have left. 1 the surface. The igûm and the igibûm what?
4Since “the thirteenth of the heap of the igûm and the igibûm
5to 6 I have repeated, from the inside of the igûm
6I have torn out: 30′ I have left,” he has said,
713, of the thirteenth, posit; 6 to which he has repeated posit;
81, the surface, posit; and 30′ which he has left posit.
9From 13, of the thirteenth, 6 to which he has repeated
10tear out. 7 you leave.
117 which you leave and 6 to which you have repeated,
12may your head hold!
137 to 6 raise, 42 to 1, the surface, raise, 42.
1442, may your head hold!
1513, of the thirteenth, to 30′ which he has left
16raise, 6°30′ to two break: 3°15′.
173°15′ together with 3°15′ make hold:
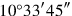 .
.
18To
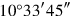 , 42 which your head holds
, 42 which your head holds
19join,
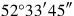 .
.
20The equal of
 what? 7°15′.
what? 7°15′.
217°15′ and 7°15′, its counterpart, lay down:
223°15′, the made-hold, from one tear out, to the other join:
23The first is 10°30, the other is 4.
24What to 7, which your head holds, should I posit
25which 10°30′ gives me? 1°30′ posit. 1°30′ to 7 raise,
2610°30′ it gives you. 1°30′ which you have posited is the igûm.
27igi 6, which your head holds, detach, 10′.
2810′ to 4 raise, 40′ is the igibûm.
29Since 1°30′ is the igûm, 40′ is the igibûm, the surface is what?
301°30′, the igûm, to 40′, the igibûm, raise, 1 is the surface.
311°30, the igûm
Rev.
1The thirteenth of 2°10′ what? 10′.
210′ to 6 repeat: 1, from 1°30,
3the igûm, tear out: 30′ you leave.
Like YBC 6967
As regards the mathematical structure and the procedure, one may compare with TMS IX #3
Str 368
Obv.
1I have taken a reed, its measure I do not know.
21 kùš I have cut off. 1 sixty (steps along) the length I have gone.
3(With) what I have cut off I have enlarged it
4with 30 (steps) of that (along) the width I have gone.
56‵15 is the surface. The head (initial length) of the reed what?
6You, by your proceeding,
71‵ and 30 posit. (For) the reed which you do not know
81 posit, to 1 sixty which you have gone
9you raise: 1‵ is the false length.
1030 to this 1 raise, 30 is the false width.
1130, the false width to 1‵, the false length,
12raise, 30‵ the false surface.
1330‵ to 6‵15, the true surface,
Rev.
1raise:
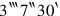 it gives you.
it gives you.
25′ which you have cut off to the false length raise,
35 it gives you. 5 to the false width raise,
42‵30 it gives you.
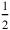 of 2‵30 break, 1‵15
of 2‵30 break, 1‵15
51‵15 make encounter,

6to
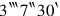 join,
join,
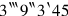 .
.
7What is equal? 13‵45 is equal.
81‵15 which you have made encounter to the inside join,
915‵ it gives you. igi 30‵, the false surface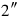 .
.
10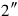 to 15‵ raise, 30′ is the head of the reed.
to 15‵ raise, 30′ is the head of the reed.
This is the rectangle version of the “broken reed”
YBC 6504 #1
Obv.
1So much as length over width goes beyond, I have made confront itself, from the inside of the surface
2I have torn it out:
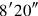 . Length over width 10′ goes beyond.
. Length over width 10′ goes beyond.
3By your proceeding, 10′ you make hold:
4 to
to
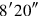 you join: 10′ you posit.
you join: 10′ you posit.
5Half of 10′ you break: 5′ you posit.
65′ you make hold:
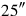 you posit.
you posit.
7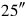 , the surface, to 10′ you join:
, the surface, to 10′ you join:
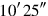 you posit.
you posit.
8By
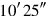 , 25′ is equal. 5′ to 25′ you join:
, 25′ is equal. 5′ to 25′ you join:
930′, the length, you posit. 5′ from 25′ your tear out:
1020′, the width, you posit.
This problem deals with the same mutilated rectangle as #4 of the same tablet (see page
In this first problem, we know the side of the square that has been “torn out.” It is therefore easily reduced to the type we know from YBC 6967
Exceptionally in this type, the “joining”
YBC 6504 #3
Rev.
1So much as length over
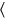 width
width
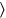 goes beyond, made encounter, from inside the surface I have torn out,
goes beyond, made encounter, from inside the surface I have torn out,
2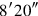 . 30′ the length, its width what?
. 30′ the length, its width what?
330′ made encounter: 15′ you posit.
4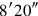 from inside 15′ you tear out,
from inside 15′ you tear out,
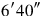 you posit.
you posit.
5Half of 30′ you break:
615′ made encounter:
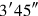 you posit.
you posit.
7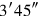 to
to
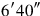 you join:
you join:
 you posit.
you posit.
8By
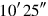 , 25′ is equal. 15′ from 25′ you tear out:
, 25′ is equal. 15′ from 25′ you tear out:
910′ you posit. 10′ from 30′ you tear out:
1020′, the width, you posit.
This is the third problem on the length leaves a remainder that can be decomposed as a square
on the length leaves a remainder that can be decomposed as a square
 and a rectangle
and a rectangle

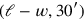 . These can be reconfigured as a gnomon, as shown in the diagram. We may look at the process as a “change of variable”—the problem now concerns a square
. These can be reconfigured as a gnomon, as shown in the diagram. We may look at the process as a “change of variable”—the problem now concerns a square
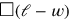 and 30 of its sides, and its solution follows the book for such problems.
and 30 of its sides, and its solution follows the book for such problems.
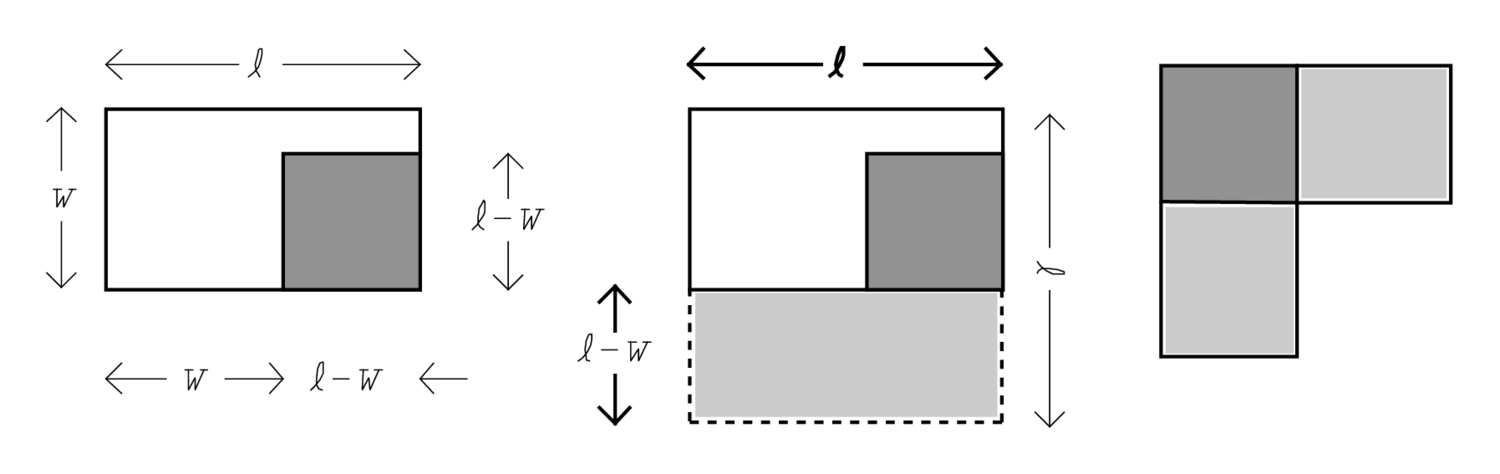
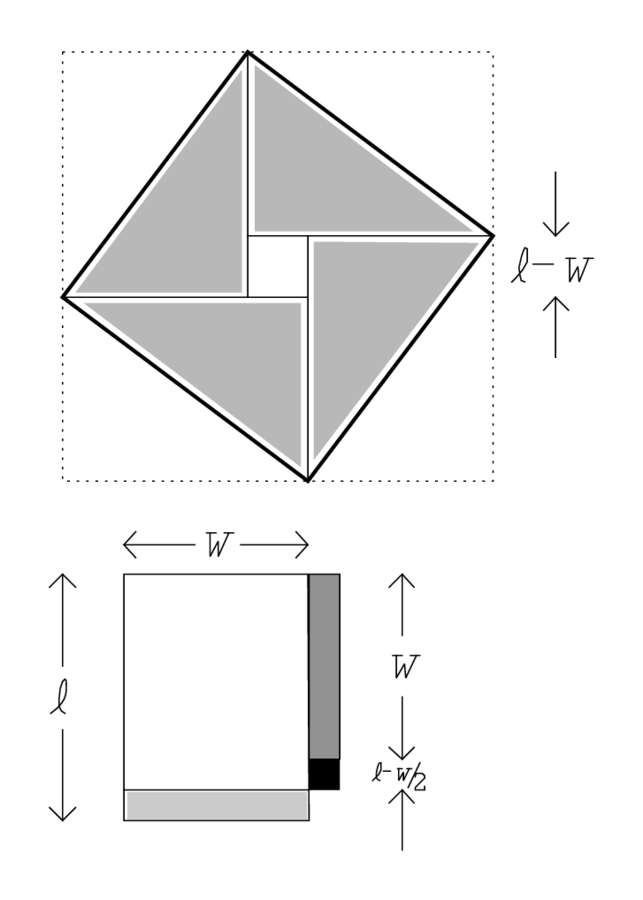
Fig. 2: The geometry behind YBC 6504 #3, in slightly distorted proportions.
BM 85200+VAT 6599 #23
Rev. I
19An excavation. So much as I have made confront itself, and 1 kùš, going beyond, that is the depth. 1°45′ of dirt I have torn out.
20You, 5′, going beyond, to 1, the conversion, raise, 5′ you see; to 12 raise, 1 you see.
215′ make confront itself,
 you see.
you see.
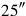 to 1 raise,
to 1 raise,
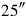 you see. igi 25 detach,
you see. igi 25 detach,
222‵24 you see. 2‵24 to 1°45′ raise, 4‵12 you see.
23from “equal, 1 joined,” 6 ¿1? is/are equal(s). 6 to 5′ raise, 30′ you see, confronts itself. 6 (error for 7) the depth.
24The procedure.
This problem comes from the same tablet as the “excavation problem”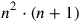 , called “equal, 1 joined.”
, called “equal, 1 joined.”
Db2–146
Obv.
1If, about a (rectangle with) diagonal, (somebody) asks you
2thus, 1°15 the diagonal, 45′ the surface;
3length and width corresponding to what? You, by your proceeding,
41°15′, your diagonal, its counterpart lay down:
5make them hold:
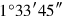 comes up,
comes up,
6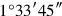 ¿may your? hand ¿hold?
¿may your? hand ¿hold?
745′ your surface to two bring: 1°30′ comes up.
8From
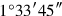 cut off: {…}
cut off: {…}
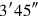 the remainder.
the remainder.
9The equal of
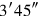 take: 15′ comes up. Its half-part,
take: 15′ comes up. Its half-part,
10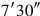 comes up, to
comes up, to
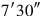 raise:
raise:
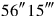 comes up
comes up
11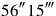 your hand. 45′ your surface over your hand,
your hand. 45′ your surface over your hand,
12 comes up. The equal of
comes up. The equal of
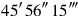 take:
take:
13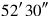 comes up,
comes up,
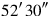 its counterpart lay down,
its counterpart lay down,
14 which you have made hold to one
which you have made hold to one
15join: from one
16cut off. 1 your length, 45 the width. If 1 the length,
1745 the width, the surface and the diagonal corresponding to what?
18You, by your making, the length make hold:
191 comes up … may your head hold.
Rev.
20… : 45′, the width, make hold:
21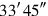 comes up. To your length join:
comes up. To your length join:
22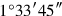 comes up. The equal of
comes up. The equal of
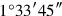 take:
take:
231°15′ comes up. 1°15′ your diagonal. Your length
24to the width raise, 45′ your surface.
25Thus the procedure.
26
This is one of the texts from the Eshnunna region, and thus belongs to the earliest phase (and as we see, it uses the phrase “to one join, from one cut off,” not respecting the “norm of concreteness”). With fair precision it can be dated to c. 1775 bce. The problem is one of the riddles which the Old Babylonian school
Lines 1–9 find the difference between the length and the width of the rectangle; the method is shown in the upper part of Figure 3. Afterwards, the sides are found from this difference and the area by the procedure which we already know perfectly well, for instance from YBC 6967
The “hand”
In the end we have a proof with an unmistakeable trace of the “Pythagorean rule” in abstract formulation (the length make hold, without the usual identification of its numerical value).
Footnotes
The tablet is damaged at this point, but the traces of signs that remain could well come from the word takkirtum, which means “change” or “modification” but does not occur in other mathematical texts. In any case, this philological doubt does not touch the interpretation of the mathematical procedure.