“Useless mathematics”
At some moment in the late 1970s, the Danish Union of Mathematics Teachers for the pre-high-school level asked its members a delicate question: to find an application of second-degree equations that fell inside the horizon of their students.
One member did find such an application: the relation between duration and counter numbers on a compact cassette reader (thus an application that at best the parents of today’s students will remember!). That was the only answer.
Many students will certainly be astonished to discover that even their teachers do not know why second-degree equations are solved. Students as well as teachers will be no less surprised that such equations have been taught since 1800 bce without any possible external reference point for the students—actually for the first 2500 years without reference to possible applications at all (only around 700 ce did Persian and Arabic astronomers possibly start to use them in trigonometric computation).
We shall return to the question why one taught, and still teaches, second-degree equations. But first we shall look at how the earliest second-degree equations, a few first-degree equations and a single cubic equation looked, and examine the way they were solved. We will need to keep in mind that even though some of the
Rudiments of General History
Mesopotamia (“Land between the rivers”) has designated since antiquity the region around the two great rivers Euphrates and Tigris—grossly, contemporary Iraq. Around 3500 bce, the water level in the Persian Gulf had fallen enough to allow large-scale irrigation agriculture in the southern part of the region, and soon the earliest
The earliest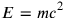 can be explained and even pronounced in any language but does not allow us to decide in which language Einstein thought). During the first half of the third millennium, however, phonetic and grammatical complements were introduced, and around 2700 bce the language was unmistakably
can be explained and even pronounced in any language but does not allow us to decide in which language Einstein thought). During the first half of the third millennium, however, phonetic and grammatical complements were introduced, and around 2700 bce the language was unmistakably
Around 2340, an Akkadian conqueror subdued the whole of Mesopotamia (Akkadian is a Semitic language, from the same language family as Arabic and Hebrew, and it had been amply present in the region at least since 2600). The Akkadian regional state lasted until c. 2200, after which followed a century of competing city states. Around 2100, the city-state of
In the long run, the bureaucracy was too costly, and around 2000 a new phase of smaller states begins. After another two centuries another phase of centralization centred around the city of Babylon sets in—from which moment it is meaningful to speak of southern and central Mesopotamia as
The phase from 2000 until the definitive collapse of the Babylonian central state around 1600 is known as the
The First Algebra and the First Interpretation
Before speaking about algebra, one should in principle know what is meant by that word. For the moment, however, we shall leave aside this question; we shall return to it in the end of the book; all we need to know for the moment is that algebra has to do with

Fig. 1.1: The cuneiform version of the problem BM 13901 #1.
Indeed, when historians of mathematics
Let us accept it in order to enter their thinking, and let us look at a very simple example extracted from a text written during the eighteenth century bce in the transliteration normally used by Assyriologists—as to the function of italics and small caps, see page
1a.šàl[am] ù mi-it-ḫar-ti ak-m[ur-m]a 45-e 1 wa-ṣi-tam
2ta-ša-ka-an ba-ma-at 1 te-ḫe-pe [3]0 ù 30 tu-uš-ta-kal
315 a-na 45 tu-ṣa-ab-ma 1-[e] 1 íb.si8 30 ša tu-uš-ta-ki-lu
4lìb-ba 1 ta-na-sà-aḫ-ma 30 mi-it-ḫar-tum
The unprepared reader, finding this complicated, should know that for the pioneers it was almost as complicated. Eighty years later we understand the technical
Cuneiform Writing
From
The signs for numbers and measures, however, were made by vertical or oblique impression of a cylindrical stylus.
With time, the character of the script changed in two ways. Firstly, instead of tracing signs consisting of curved lines one impressed them with a stylus with sharp edges, dissolving the curved lines into a sequence of straight segments. In this way, the signs seem to be composed of small wedges (whence the name “cuneiform”).
In the second half of the third millennium, numerical and metrological signs came to be written in the same way. The signs became increasingly stylized, loosing their pictographic quality; it is then not possible to guess the underlying drawing unless one knows the historical
Let us for instance look at the character which initially depicted a vase with a spout (left).
In
The other change concerns the use of the way the signs were used (which implies that we should better speak of them as “characters”). The Sumerian word for the vase is dug. As various literary genres developed alongside accounting (for instance, royal inscriptions, contracts and proverb collections), the scribes needed ways to write syllables that serve to indicate grammatical declinations or proper nouns. This
Words to be read as
Assyriologists distinguish
It was already known that these numbers were written in a place-value system with base 60 but without indication of absolute order of magnitude (see the box  ). Let us therefore try to
). Let us therefore try to
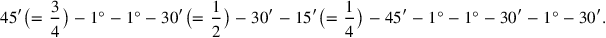
|
In order to make the next step one needs some fantasy. Noticing that
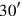 is
is
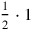 and
and
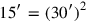 we may think of the equation
we may think of the equation
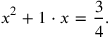
|
Today we solve it in these steps (neglecting negative numbers, a modern invention):
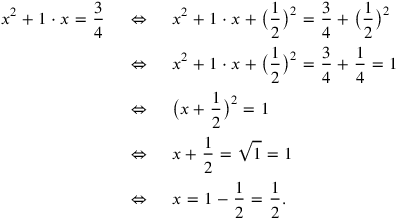
|
As we see, the method is based on addition, to both sides of the equation, of the square on half the coefficient of the first-degree term
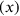 —here
—here
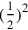 . That allows us to rewrite the left-hand side as the square on a binomial:
. That allows us to rewrite the left-hand side as the square on a binomial:
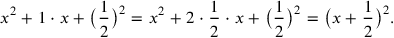
|
This small trick is called a
Comparing the ancient text and the modern solution we notice that the same numbers occur in almost the same order. The same holds for many other texts. In the early 1930s historians of mathematics thus became convinced that between 1800 and 1600 bce the Babylonian scribes knew something very similar to our equation algebra. This period constitutes the second half of what is known as the “Old Babylonian” epoch (see the box “Rudiments of General History,” page
The next step was to 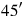 and
and
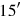 (that is, of
(that is, of
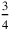 and
and
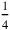 ) produces 1. When other texts
) produces 1. When other texts
In this way, the scholars of the 1930s came to choose a purely
1I have added the surface and (the side of) my square: 45′.
2You posit 1°, the unit. You break into two
 . You multiply (with each other) [30′] and 30′:
. You multiply (with each other) [30′] and 30′:
315′. You join
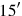 to
to
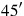 : 1°.
: 1°.
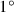 is the square of
is the square of
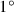 . 30′, which you have multiplied (by itself),
. 30′, which you have multiplied (by itself),
4from
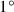 you subtract:
you subtract:
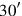 is the (side of the) square.
is the (side of the) square.
Such translations are still found today in general histories of mathematics. They explain the numbers that occur in the texts, and they give an almost modern impression of the Old Babylonian methods. There is no fundamental difference between the above translation and the solution by means of equations. If the side of the square is
 , then its area is
, then its area is
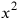 . Therefore, the first line of the text—the problem to be solved—corresponds to the equation
. Therefore, the first line of the text—the problem to be solved—corresponds to the equation
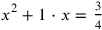 . Continuing the reading of the translation we see that it follows the symbolic transformations on page
. Continuing the reading of the translation we see that it follows the symbolic transformations on page
However, even though the present translation as well as others made according to the same principles explain the numbers of the texts, they agree less well with their words, and sometimes not with the order of operations. Firstly, these translations do not take the geometrical character of the terminology into account, supposing that words and expressions like “(the side of) my square,” “length,” “width” and “area” of a rectangle denote nothing but unknown numbers and their products. It must be recognized that in the 1930s that did not seem impossible a priori—we too speak of
 as the “square of 3” without thinking of a quadrangle.
as the “square of 3” without thinking of a quadrangle.
But there are other problems.
The Sexagesimal Place-Value System
The Old Babylonian mathematical texts make use of a place-value with no indication of a “sexagesimal point.” In our notation, which also employs place value, the digit “
with no indication of a “sexagesimal point.” In our notation, which also employs place value, the digit “
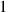 ” may certainly represent the number
” may certainly represent the number
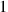 , but also the numbers
, but also the numbers
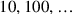 , as well as
, as well as
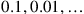 . Its value is determined by its distance from the decimal point.
. Its value is determined by its distance from the decimal point.
Similarly, “
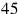 ” written by a Babylonian scribe may mean
” written by a Babylonian scribe may mean
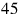 ; but it may also stand for
; but it may also stand for
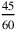 (thus
(thus
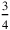 ); for
); for
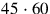 ; etc. No decimal point determines its “true” value. The system corresponds to the slide rule of which engineers made use before the arrival of the electronic pocket calculator. This device also had no decimal point, and thus did not indicate the absolute order of magnitude. In order to know whether a specific construction would ask for
; etc. No decimal point determines its “true” value. The system corresponds to the slide rule of which engineers made use before the arrival of the electronic pocket calculator. This device also had no decimal point, and thus did not indicate the absolute order of magnitude. In order to know whether a specific construction would ask for
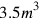 ,
,
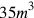 or
or
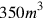 of concrete, the engineer had recourse to mental calculation.
of concrete, the engineer had recourse to mental calculation.
For writing numbers between 1 and 59, the Babylonians made use of a vertical wedge (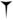 ) repeated until 9 times in fixed patterns for the numbers 1 to 9, and of a Winkelhaken (a German loanword originally meaning “angular hook”) (
) repeated until 9 times in fixed patterns for the numbers 1 to 9, and of a Winkelhaken (a German loanword originally meaning “angular hook”) ( ) repeated until 5 times for the
) repeated until 5 times for the 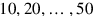 .
.
A modern reader is not accustomed to reading numbers with undetermined order of magnitude. In translations of Babylonian mathematical texts it is therefore customary to indicate the order of magnitude that has to be attributed to numbers. Several methods to do that are in use. In the present work we shall employ a generalization of the degree-minute-second notation. If  means
means
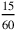 , we shall transcribe it
, we shall transcribe it
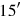 , if it corresponds to
, if it corresponds to
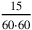 , we shall write
, we shall write
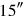 . If it represents
. If it represents
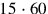 , we write
, we write
 , etc. If it stands for
, etc. If it stands for
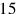 , we write
, we write
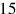 or, if that is needed in order to avoid misunderstandings,
or, if that is needed in order to avoid misunderstandings,
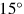 .
. 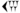 understood as
understood as
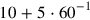 will thus be transcribed
will thus be transcribed

 understood as
understood as
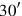 thus means
thus means
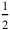 .
.
 understood as
understood as
 means
means
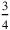 .
.
 understood as
understood as
 means
means
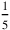 ; understood as
; understood as
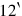 it means
it means
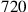 .
.
 understood as
understood as
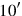 means
means
 .
.
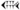 may mean
may mean
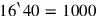 or
or
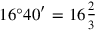 , etc.
, etc.
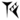 may mean
may mean
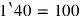 ,
,
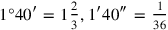 , etc.
, etc.
Outside school, the Babylonians employed the place-value system exclusively for intermediate calculations (exactly as an engineer used the slide rule fifty years ago). When a result was to be inserted into a contract or an account, they could obviously not allow themselves to be ambiguous; other notations allowed them to express the precise number they intended.
Certainly, we too know about
Synonyms, it is true, can also be found in Old Babylonian mathematics. Thus, the verbs “to tear out”
A translation which mixes up operations which the Babylonians treated as distinct may explain why the Babylonian calculations lead to correct results; but it cannot penetrate their mathematical thought.
Further, the traditional translations had to skip certain words which seemed to make no sense. ” (or even “from the heart” or “from the bowels”). Not seeing how a number 1 could possess an
” (or even “from the heart” or “from the bowels”). Not seeing how a number 1 could possess an
Other words were translated in a way that differs so strongly from their normal meaning that it must arouse suspicion.
Finally, the order in which operations are performed is sometimes different from what seems natural in the arithmetical reading.
In spite of these objections, the interpretation
A New Reading
As we have just seen, the arithmetical interpretation is unable to account for the words which the Babylonians used to describe their procedures. Firstly, it conflates operations that the Babylonians treated as distinct; secondly, it is based on operations whose order does not always correspond to that of the Babylonian calculations. Strictly speaking, rather than an interpretation it thus represents a control of the correctness of the Babylonian methods based on modern techniques.
A genuine interpretation
In the following chapters we are going to analyze a number of problems in a translation that corresponds to such an interpretation. First some general information will be adequate.
In our algebra we use x and y as substitutes or names for unknown numbers. We use this algebra as a tool for solving problems that concern other kinds of magnitudes, such as prices, distances, energy densities, etc.; but in all such cases we consider these other quantities as represented by numbers. For us, numbers constitute the fundamental representation
With the Babylonians, the fundamental representation
An important characteristic of Babylonian geometry allows it to serve as an “algebraic” representation: it always deals with measured quantities. The measure of its segments and areas may be treated as unknown—but even then it exists as a numerical measure, and the problem consists in finding its value.
Every measuring operation presupposes a metrology, a system of measuring units; the numbers that result from it are concrete numbers. That cannot be seen directly in the problem that was quoted above on page
The standard unit for horizontal distance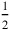 nindan, that is, c. 3 m. For vertical distances
nindan, that is, c. 3 m. For vertical distances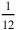 nindan (that is, c. 50 cm).
nindan (that is, c. 50 cm).
The standard unit for areas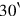 sar
sar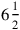 ha.
ha.
The standard unit for hollow measures
Finally, the standard unit for weights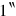 shekel, c. 30 kilogram. This last unit is equal to the talent of the Bible (where a talent
shekel, c. 30 kilogram. This last unit is equal to the talent of the Bible (where a talent
There are two additive operations
“Heaping,”
The sum resulting from a “joining”
There are also two subtractive operations
The difference in the first subtraction is called “the remainder”
There are several synonyms or near-synonyms for “tearing out.” We shall encounter “cutting off” (ḫarāṣum) (AO 8862 #2, page
Four distinct operations
First, there is the one which appears in the Old Babylonian version of the multiplication table. The Sumerian term (a.rá, derived from the Sumerian verb rá, “to go”) can be translated “steps of.”
1 step of 6 is 6
2 steps of 6 are 12
3 steps of 6 are 18
…
Three of the texts we are to encounter below (TMS VII #2 (TMS VII #2, line 18; TMS IX #3, line 21); TMS VIII #1 line 1 joins a magnitude s n times to another magnitude
(TMS VII #2, line 18; TMS IX #3, line 21); TMS VIII #1 line 1 joins a magnitude s n times to another magnitude
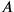 , with outcome
, with outcome
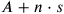 .
.
The second “multiplication” is defined by the verb “to raise”
The third “multiplication” (šutakūlum/gu7.gu7), “to make
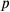 and
and
 hold each other”—or simply, because that is almost certainly what the Babylonians thought of, “make
hold each other”—or simply, because that is almost certainly what the Babylonians thought of, “make
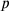 and
and
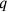 hold
hold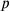 and
and
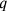 , and “to make
, and “to make
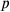 and
and
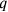 hold” means to construct a rectangle contained by the sides
hold” means to construct a rectangle contained by the sides
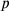 and
and
 . Since
. Since
 and
and
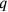 as well as the area
as well as the area
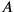 of the rectangle are all measurable, almost all texts give the numerical value of
of the rectangle are all measurable, almost all texts give the numerical value of
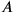 immediately after prescribing the operation—“make 5 and 5 hold: 25”—without mentioning the numerical multiplication of 5 by 5 explicitly. But there are texts that speak separately about the numerical multiplication, as “
immediately after prescribing the operation—“make 5 and 5 hold: 25”—without mentioning the numerical multiplication of 5 by 5 explicitly. But there are texts that speak separately about the numerical multiplication, as “
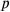 steps of
steps of
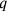 ,” after prescribing the construction, or which indicate that the process of “making hold” creates “a surface”
,” after prescribing the construction, or which indicate that the process of “making hold” creates “a surface”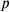 and
and
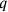 by the symbol
by the symbol
 (
(
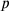 ,
,
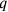 ), while
), while
 (
(
 ) will stand for the square which a segment a “holds together with itself” (in both cases, the symbol designates the configuration as well the area it contains, in agreement with the ambiguity inherent in the concept of “surface”). The corresponding numerical multiplications will be written symbolically as
) will stand for the square which a segment a “holds together with itself” (in both cases, the symbol designates the configuration as well the area it contains, in agreement with the ambiguity inherent in the concept of “surface”). The corresponding numerical multiplications will be written symbolically as

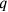 and
and

 .
.
The last “multiplication” (eṣēpum) is also no proper numerical multiplication. “To repeat” or “to repeat until
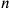 ” (where
” (where
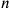 is an integer small enough to be easily imagined, at most 9) stands for a “physical” doubling or
is an integer small enough to be easily imagined, at most 9) stands for a “physical” doubling or
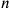 -doubling—for example that doubling of a right triangle with sides (containing the right angle)
-doubling—for example that doubling of a right triangle with sides (containing the right angle)
 and
and
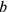 which produces a rectangle
which produces a rectangle
 (
(
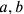 ).
).
The problem “what should I raise to d in order to get P?” is a division problem, with answer
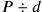 . Obviously, the Old Babylonian calculators knew such problems perfectly well. They encountered them in their “algebra” (we shall see many examples below) but also in practical planning: a worker can dig N nindan irrigation canal in a day; how many workers will be needed for the digging of 30 nindan in 4 days? In this example the problem even occurs twice, the answer being
. Obviously, the Old Babylonian calculators knew such problems perfectly well. They encountered them in their “algebra” (we shall see many examples below) but also in practical planning: a worker can dig N nindan irrigation canal in a day; how many workers will be needed for the digging of 30 nindan in 4 days? In this example the problem even occurs twice, the answer being
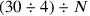 . But division
. But division
In order to divide 30 by 4, they first used a table (see Figure 1.2), in which they could read (but they had probably learned it by heart 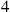 is
is
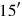 ; afterwards they “raised”
; afterwards they “raised”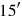 to
to
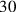 (even for that tables existed, learned by heart
(even for that tables existed, learned by heart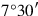 .9
.9

Fig. 1.2: Translation of the Old Babylonian table
Primarily , igi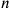 stands for the reciprocal of n as listed in the table or at least as easily found from it, not the number
stands for the reciprocal of n as listed in the table or at least as easily found from it, not the number
 abstractly. In this way, the Babylonians solved the problem
abstractly. In this way, the Babylonians solved the problem
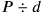 via a multiplication
via a multiplication 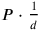 to the extent that this was possible.
to the extent that this was possible.
However, this was only possible if
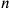 appeared in the igi
appeared in the igi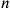 was a “regular number,”
was a “regular number,”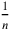 could be written as a finite “sexagesimal fraction.”
could be written as a finite “sexagesimal fraction.”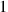
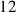 ,
,
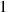
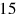 and
and
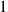
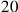 are omitted “to the left” since they are already present “to the right”).
are omitted “to the left” since they are already present “to the right”).
In practical computation, that was generally enough. It was indeed presupposed that all technical constants—for example, the quantity of dirt a worker could dig out in a day—were simple regular numbers. The solution of “algebraic” problems, on the other hand, often leads to divisions by a non-regular divisor
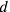 . In such cases, the texts write “what shall I posit to
. In such cases, the texts write “what shall I posit to
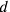 which gives me
which gives me
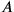 ?”, giving immediately the answer “posit
?”, giving immediately the answer “posit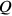 ,
,
 will it give you.”11 That has a very natural explanation: these problems were constructed backwards, from known results. Divisors would therefore always divide, and the teacher who constructed a problem already knew the answer as well as the outcome of divisions leading to it.
will it give you.”11 That has a very natural explanation: these problems were constructed backwards, from known results. Divisors would therefore always divide, and the teacher who constructed a problem already knew the answer as well as the outcome of divisions leading to it.
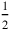 may be a fraction like any other:
may be a fraction like any other:
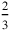 ,
,
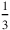 ,
,
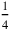 , etc. This kind of half, if it is the half of something, is found by raising that thing to 30′. Similarly, its
, etc. This kind of half, if it is the half of something, is found by raising that thing to 30′. Similarly, its
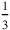 is found by raising to 20′, etc. This kind of half we shall meet in AO 8862 #2
is found by raising to 20′, etc. This kind of half we shall meet in AO 8862 #2
But
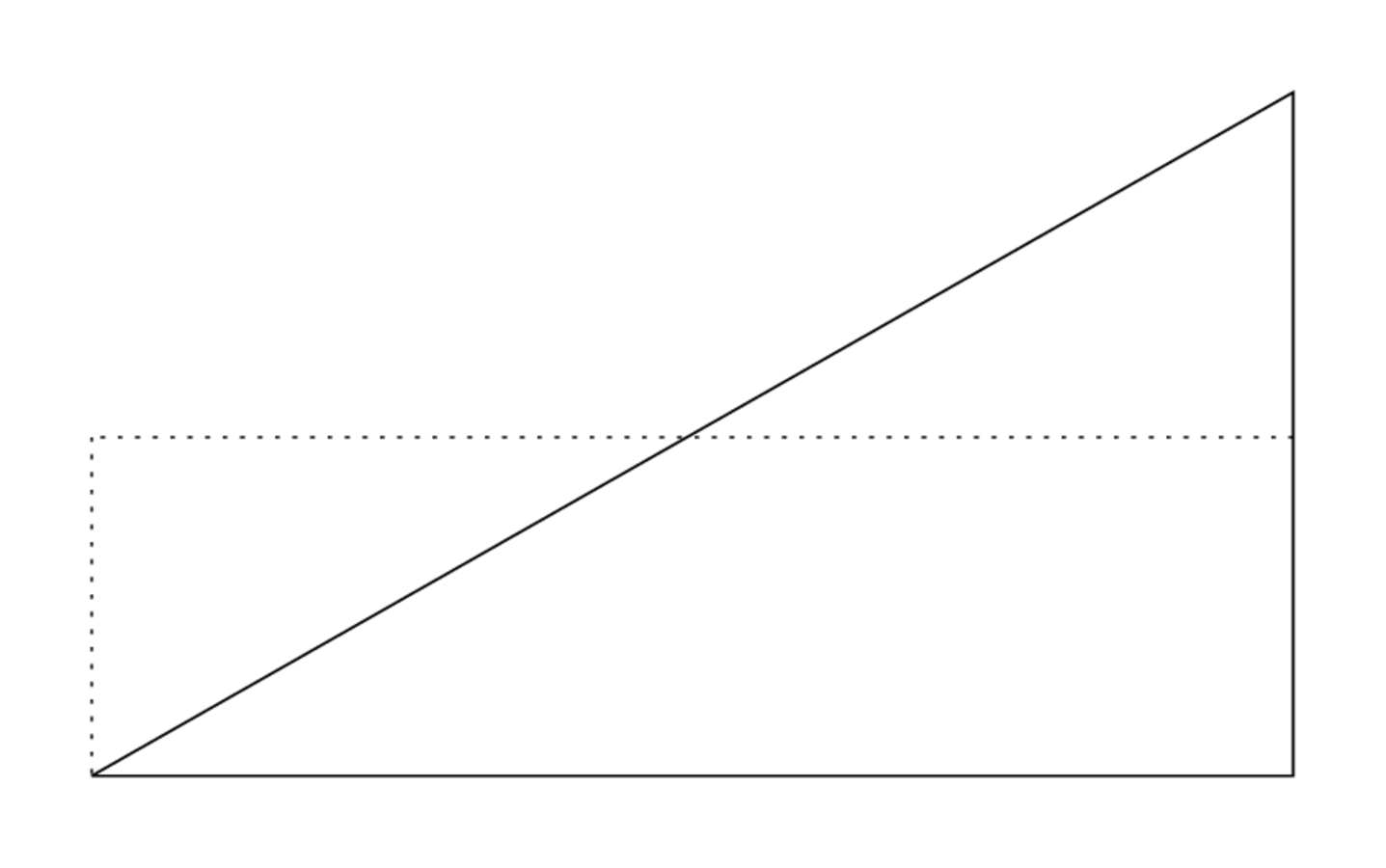
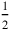 (in this case necessarily the half of something) may also be a “natural” or “necessary” half, that is, a half that could be nothing else. The radius of a circle is thus the “natural” half of the diameter: no other part could have the same role. Similarly, it is by necessity the exact half of the base that must be raised to the height of a triangle in order to give the area—as can be seen on the figure used to prove the formula (see Figure 1.3).
(in this case necessarily the half of something) may also be a “natural” or “necessary” half, that is, a half that could be nothing else. The radius of a circle is thus the “natural” half of the diameter: no other part could have the same role. Similarly, it is by necessity the exact half of the base that must be raised to the height of a triangle in order to give the area—as can be seen on the figure used to prove the formula (see Figure 1.3).
This “natural” half had a particular name (bāmtum), which we may translate “moiety.”
The product
 played no particular role, neither when resulting from a “raising”
played no particular role, neither when resulting from a “raising”
But the geometric square did have a particular status. One might certainly “make a and a hold” or “make a together with itself hold
In order to say that s is the side of a square area Q, a Sumerian phrase (used already in tables of inverse squares probably going back to Ur III
Just as there were tables
Concerning the Texts and the Translations
The texts that are presented and explained in the following are written in Babylonian, the language
As already indicated, our texts come from the second half of the Old Babylonian epoch, as can be seen from the handwriting and the language. Unfortunately it is often impossible to say more, since almost all of them come from illegal diggings and have been bought by museums on the antiquity market in Baghdad or Europe.
We have no direct information about the authors of the texts. They never present themselves, and no other source speaks of them. Since they knew how to write (and more than the rudimentary syllabic of certain laymen), they must have belonged to the broad category of scribes
All this, however, results from indirect arguments. Plausibly, the majority of scribes never produced mathematics on their own beyond simple computation; few were probably ever trained at the high mathematical level presented by our texts. It is even likely that only a minority of school teachers taught such matters. In consequence, and because several voices speak through the texts (see page
The English translations that follow—all due to the author of the book—do not distinguish between syllabically and logographically written words (readers who want to know must consult the transliterations in Appendix B). Apart from that, they are “conformal”
This is not to say that the Babylonians did not have a technical terminology but only their everyday language; but it is important that the technical meaning of a word be learned from its uses within the Old Babylonian texts and not borrowed (with the risk of being badly borrowed, as has often happened) from our modern terminology.
The Babylonian language structure is rather different from that of English, for which reason the conformal
In order to avoid completely illegible translations, the principle
Inscribed clay survives better than paper—particularly well when the city burns together with its libraries and archives, but also when discarded as garbage. None the less, almost all the tablets
Clay tablets have names, most often museum numbers. The small problem quoted above is the first one on the tablet BM 13901—that is, tablet #13901 in the British Museum tablet collection. Other names begin AO (Ancient Orient, Louvre, Paris), VAT (Vorderasiatische Texte, Berlin) or YBC (Yale Babylonian texts). TMS refers to the edition Textes mathématiques de Suse of a Louvre collection of tablets from Susa, an Iranian site in the eastern neighborhood of Babylon.
The tablets are mostly inscribed on both surfaces (“obverse” and “reverse”), sometimes in several columns, sometimes also on the edge; the texts are divided in lines read from left to right. Following the original editions, the translations indicate line numbers and, if actual, obverse/reverse and column.
Footnotes
However, around 1930 one had to begin with texts that were much more complex than the one we consider here, which was only discovered in 1936. But the principles were the same. The most important contributions in the early years were due to Otto Neugebauer, historian of ancient mathematics and astronomy, and the Assyriologist François Thureau-Dangin.
A literal retranslation of François Thureau-Dangin’s French translation. Otto Neugebauer’s German translation is equivalent except on one point: where Thureau-Dangin translated “1°, the unit” Neugebauer proposed “1, the coefficient.” He also transcribed place-value numbers differently.
Nobody, except perhaps Neugebauer, who on one occasion observes (correctly) that a text makes use of a wrong multiplication. In any case it must be noticed that neither he nor Thureau-Dangin ever chooses a wrong operation when restituting the missing part of a broken text.
More precisely, the word translated “length” signifies “distance”/“extension”/“length” while that which is translated “width” means “front”/“forehead”/“head.” They refer to the idea of a long and narrow irrigated field. The word for the area (eqlum/a.šà) originally means “field” but in order to reserve it for technical use the texts use other (less adequate) words when speaking of genuine fields to be divided. In what follows, the term will be translated “surface,” which has undergone a similar shift of meaning, and which stands both for the spatial entity and its area.
A similar distinction is created by other means for lengths and widths. If these stand for “algebraic” variables they are invariably written with the logograms uš and sag̃; if used for general purposes (the length of a wall, a walking distance) they may be provided with phonetic complements or written syllabically as šiddum and pūtum .
In the absence of a sexagesimal point it is in principle impossible to know whether the basic unit was 1 nindan, 60 nindan or
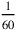 nindan. The choice of 1 nindan represents what (for us, at least) seems most natural for an Old Babylonian calculator, since it already exists as a unit (which is also true for 60 nindan but not for
nindan. The choice of 1 nindan represents what (for us, at least) seems most natural for an Old Babylonian calculator, since it already exists as a unit (which is also true for 60 nindan but not for
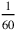 nindan) and because distances measured in nindan had been written without explicit reference to the unit for centuries before the introduction of the place-value system.
nindan) and because distances measured in nindan had been written without explicit reference to the unit for centuries before the introduction of the place-value system.
It is not to be excluded that the Babylonians thought of the mina as standard unit, or that they kept both possibilities open.
The verbal form used would normally be causative-reciprocative. However, at times the phrase used is “make p together with q hold” which seems to exclude the reciprocative interpretation.
When speaking of a “school” in the Old Babylonian context we should be aware that we only know it from textual evidence. No schoolroom has been identified by archaeologists (what was once believed to be school rooms has turned out to be for instance store rooms). We therefore do not know whether the scribes were taught in palace or temple schools or in the private homes of a master scribe instructing a handful of students; most likely, many were taught by private masters. The great number of quasi-identical copies of the table of reciprocals that were prepared in order to be learned by heart show, however, that future scribes were not (or not solely) taught as apprentices of a working scribe but according to a precisely defined curriculum; this is also shown by other sources.
It may seem strange that the multiplication of igi 4 by 30 is done by “raising.” Is this not a multiplication of a number by a number? Not necessarily, according the expression used in the texts when igi 4 has to be found: they “detach” it. The idea is thus a splitting into 4 equal parts, one of which is detached. It seems that what was originally split (when the place-value system was constructed) was a length—namely 1‵ [nindan], not 1 [nindan]. This Ur-III understanding had certainly been left behind; but the terminological habit had survived.
And, tacitly understood, that n itself can be written in this way. It is not difficult to show that all “regular numbers” can be written
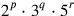 , where p, q and r are positive or negative integers or zero.
, where p, q and r are positive or negative integers or zero.
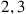 and
and
 are indeed the only prime numbers that divide 60. Similarly, the “regular numbers” in our decimal system are those that can be written
are indeed the only prime numbers that divide 60. Similarly, the “regular numbers” in our decimal system are those that can be written
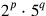 , 2 and 5 being the only prime divisors of 10.
, 2 and 5 being the only prime divisors of 10.
The expression “posit to” refers to the way simple multiplication exercises were written in school: the two factors were written one above the other (the second being “posited to” the first), and the result below both.
More precisely, the Babylonian word stands for “a situation characterized by the confrontation of equals.”
In Akkadian, the verb comes in the end of the phrase. This structure allows a number to be written a single time, first as the outcome of one calculation and next as the object of another one. In order to conserve this architecture of the text (“number(s)/operation: resulting number/new operation”), this final position of the verb is respected in the translations, ungrammatical though it is. The reader will need to get accustomed (but non-English readers should not learn it so well as to use the construction independently!).