TMS IX #3
19Surface, length, and width I have heaped, 1 the surface. 3 lengths, 4 widths heaped,
20its 17th to the width joined, 30′.
21You, 30′ to 17 go: 8°30′ you see.
22To 17 widths 4 widths join, 21 you see.
2321 as much as of widths posit. 3, of three lengths,
243, as much as of lengths posit. 8°30′, what is its name?
253 lengths and 21 widths heaped.
26 8°30′ you see,
27 3 lengths and 21 widths heaped.
28Since 1 to the length is joined and 1 to the width is joined, make hold:
291 to the heap of surface, length, and width join, 2 you see,
302 the surface. Since the length and the width of 2 the surface,
311°30′, the length, together with 1°20′, the width, are made hold,
321 the joined of the length and 1 the joined of the width,
33make hold, ¿1 you see.? 1 and 1, the various (things), heap, 2 you see.
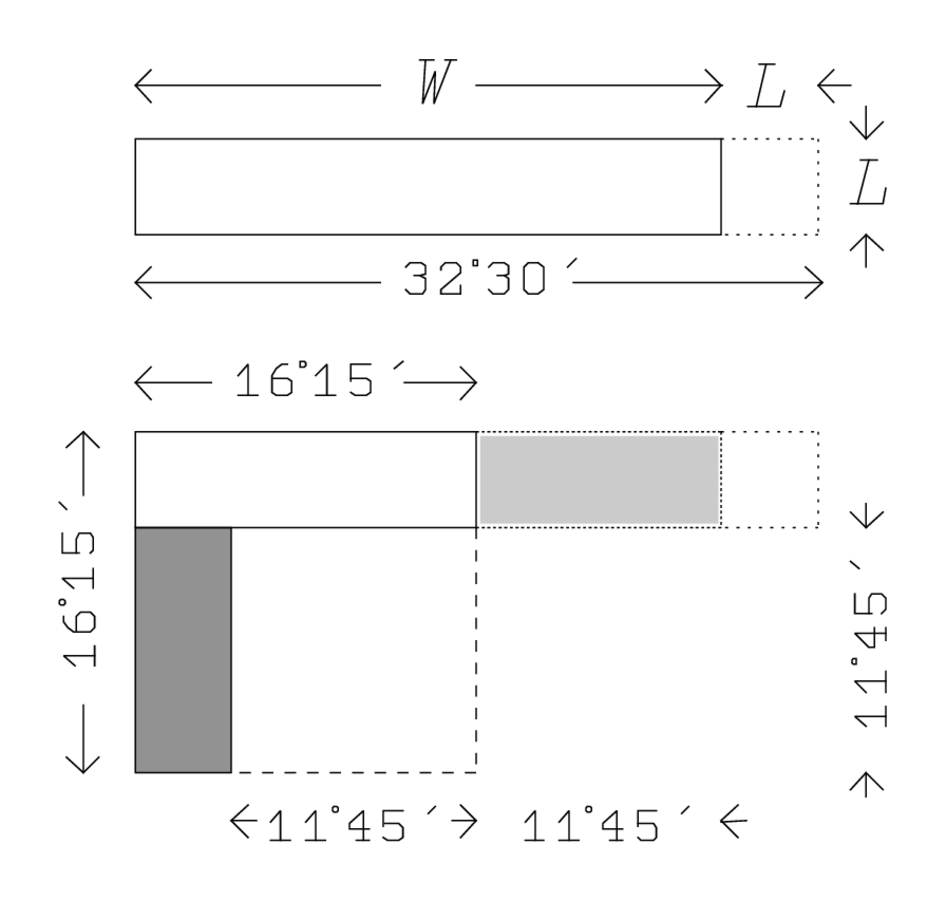
343…, 21…, and 8°30′ heap, 32°30′ you see;
35so you ask.
36… of widths, to 21, that heap:
37… to 3, lengths, raise,
381‵3 you see. 1‵3 to 2, the surface, raise:
392‵6 you see, ¿2‵6 the surface?. 32°30′ the heap break, 16°15′ you
 see
see
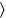 .
.
40{…}. 16°15′ the counterpart posit, make hold,
41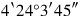 you see. 2‵6 ¿erasure?
you see. 2‵6 ¿erasure?
42from
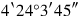 tear out,
tear out,
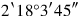 you see.
you see.
43What is equal? 11°45′ is equal, 11°45′ to 16°15′ join,
4428 you see. From the 2nd tear out, 4°30′ you see.
45igi 3, of the lengths, detach, 20′ you see. 20′ to 4°30′
46{…} raise: 1°30′ you see,
471°30′ the length of 2 the surface. What to 21, the widths, may I posit
48which 28 gives me? 1°20′ posit, 1°20′ the width
49of 2 the surface. Turn back. 1 from 1°30′ tear out,
5030′ you see. 1 from 1°20′ tear out,
5120′ you see.
Lines 19 and 20 present a system of two equations about a rectangle, one of the first and one of the second degree. The former is of the same type as the one explained in TMS XVI #1

|
In agreement with what we have seen elsewhere, the text multiplies the first-degree equation by 17 (using the Akkadian verb “to go,”
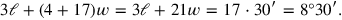
|
This is done in the lines 21–25, while the lines 26 and 27 summarize the result.
Lines 28–30 repeat the trick used in section #2 of the text (see Figure 3.10): the length and the width are prolonged by 1, and the square that is produced when that which the two “joined”1 “hold” is “joined” to the “heap”
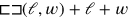 ; out of this comes a “surface 2,” the meaning of which is again explained in lines 30–33.
; out of this comes a “surface 2,” the meaning of which is again explained in lines 30–33.
The lines 34–37 are very damaged, too damaged to be safely reconstructed as far as their words are concerned. However, the numbers suffice to see how the calculations proceed. Let us introduce the magnitudes
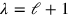 and
and
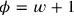 . The text refers to them as the length and width “of the surface 2”—in other words,
. The text refers to them as the length and width “of the surface 2”—in other words,
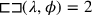 . Further,
. Further,
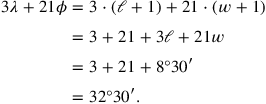
|
In order to facilitate the understanding of what now follows we may further introduce the variables
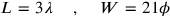
|
(but we must remember that the text has no particular names for these—in contrast to
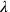 and
and
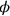 which do have names; we now speak about, not
which do have names; we now speak about, not
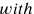 the Babylonian author). Lines 36–39 find that
the Babylonian author). Lines 36–39 find that
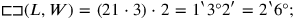
|
summing up we thus have
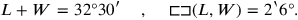
|
We have now come to line 39, and arrived at a problem type which we had not seen so far: A rectangle for which we know the area and the sum of the two sides.
Once again, a cut-and-paste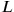 and
and
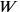 . This rectangle is composed from
. This rectangle is composed from
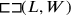 , traced in full, and a square
, traced in full, and a square
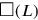 to its right, drawn with a dotted line. Next, we let the two “moieties” of this segment “hold” a square (lines 39–40). As we see, that part of the original rectangle
to its right, drawn with a dotted line. Next, we let the two “moieties” of this segment “hold” a square (lines 39–40). As we see, that part of the original rectangle
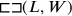 which falls outside the new square can just be fitted into it so as to form a gnomon together with that part which stays in place. In its original position, this piece appears in light shading, whereas it is darkly shaded in its new position.
which falls outside the new square can just be fitted into it so as to form a gnomon together with that part which stays in place. In its original position, this piece appears in light shading, whereas it is darkly shaded in its new position.
One part of the new square
 (16°15′) is constituted by the gnomon, whose area results from recombination of the original rectangle
(16°15′) is constituted by the gnomon, whose area results from recombination of the original rectangle
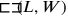 ; this area is hence 2‵6. We also know the area of the outer square,
; this area is hence 2‵6. We also know the area of the outer square,
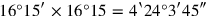 (lines 40 and 41). When the gnomon is “torn out” (lines 41 and 42),
(lines 40 and 41). When the gnomon is “torn out” (lines 41 and 42),
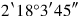 remains for the square contained by the gnomon. Its side (that which “is equal”) is 11°45′, which must now be “joined” to one of the pieces 16°15′ (which gives us
remains for the square contained by the gnomon. Its side (that which “is equal”) is 11°45′, which must now be “joined” to one of the pieces 16°15′ (which gives us
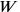 ) and “torn out” from the other, its “counterpart” (which gives us
) and “torn out” from the other, its “counterpart” (which gives us
 ). This time, however, it is not the same piece that is “joined”
). This time, however, it is not the same piece that is “joined”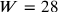 and
and
 . Finally, the text determines first
. Finally, the text determines first
 and
and
 and then
and then
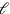 and
and
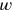 —we remember that
—we remember that
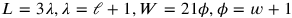 . Since 28 has no igi, line 48 explains that
. Since 28 has no igi, line 48 explains that
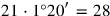 .
.
AO 8862 #2
I
30Length, width. Length and width
31I have made hold: A surface I have built.
32I turned around (it). The half of the length
33and the third of the width
34to the inside of my surface
35I have joined: 15.
36I turned back. Length and width
37I have heaped: 7.
II
1Length and width what?
2You, by your proceeding,
32 (as) inscription of the half
4and 3 (as) inscription
5of the third you inscribe:
6igi 2, 30′, you detach:
730′ steps of 7, 3°30′; to 7,
8the things heaped, length and width,
9I bring:
103°30′ from 15, my things heaped,
11cut off:
1211°30′ the remainder.
13Do not go beyond. 2 and 3 make hold:
143 steps of 2, 6.
15igi 6, 10′ it gives you.
1610′ from 7, your things heaped,
17length and width, I tear out:
186°50′ the remainder.
19Its moiety, that of 6°50′, I break:
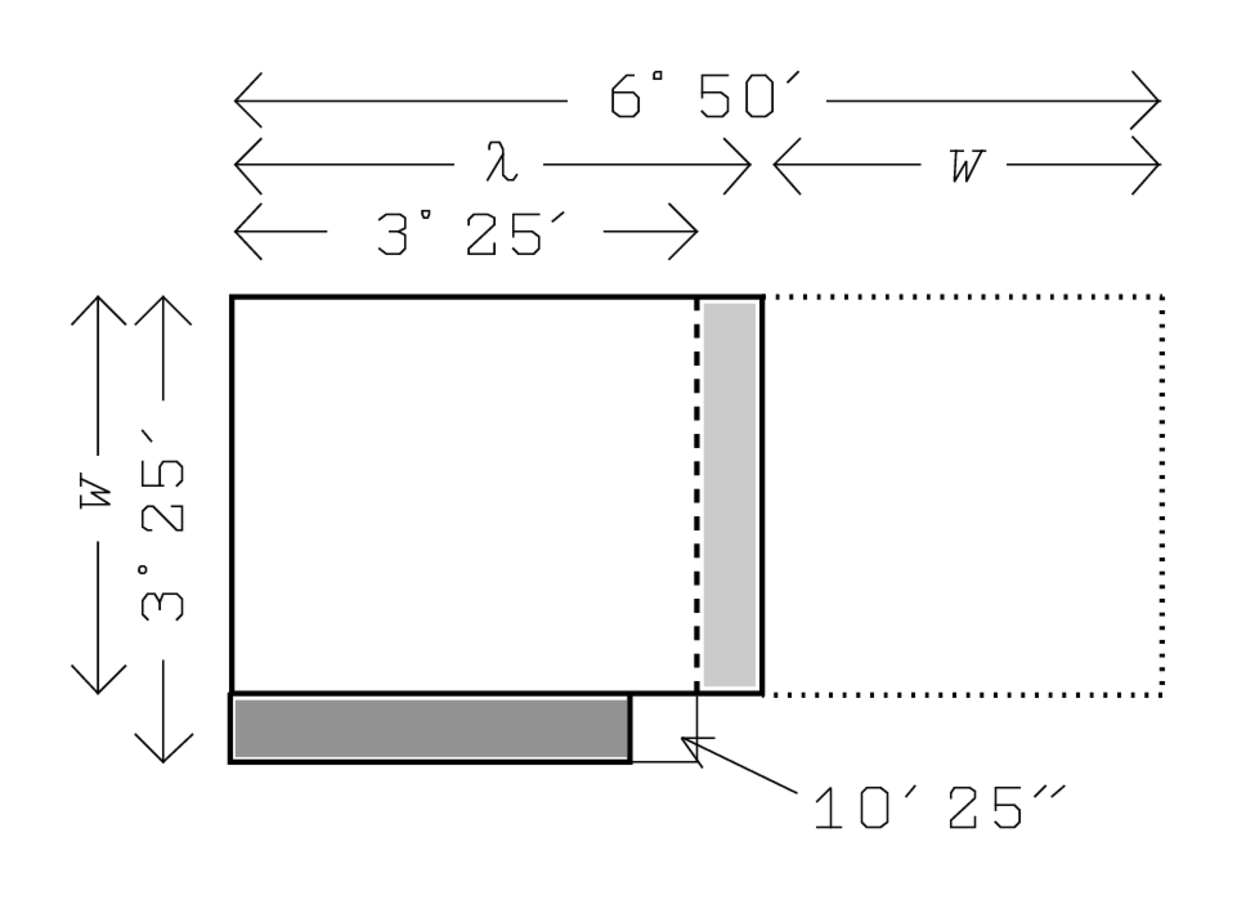
203°25′ it gives you.
213°25′ until twice
22you inscribe; 3°25′ steps of 3°25′,
23 ; from the inside
; from the inside
2411°30′ I tear out:
25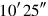 the remainder.
the remainder.
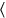 By
By
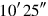 , 25′ is equal
, 25′ is equal
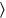 .
.
26To the first 3°25′
2725′ you join: 3°50′,
28and (that) which from the things heaped of
29length and width I have torn out
30to 3°50′ you join:
314 the length. From the second 3°25′
3225′ I tear out: 3 the width.
337 the things heaped.
344, the length; 3, the width; 12, the surface.
The first two words of the first line (I.30) tell us that we are dealing with a figure that is fully characterized by its length and its width, that is, with a rectangle (cf. page
Before studying the procedure, we may concentrate on certain aspects of the formulation of the text. In line I.31 we see that the operation “to make hold”
The text, almost certainly from Larsa, seems to be from c. 1750 bce and thus to belong to the early phase of the adoption of algebra by the southern scribe school
The topic of the problem is thus a rectangle. Lines I.36–37 tell us that the “heap” of its length and width is 7, while the lines I.32–35 state that “joining” half of the length and one third of the width to the “surface” produces 15:2
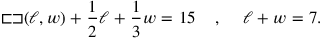
|
The upper part of Figure 4.2 illustrates this situation, with 2 and 3 “inscribed as inscription” of
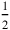 respectively
respectively
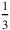 of the “projections”3 1 of the length and the width (lines II.2–5); the heavily drawn configuration thus has an area equal to 15.
of the “projections”3 1 of the length and the width (lines II.2–5); the heavily drawn configuration thus has an area equal to 15.
The solution could have followed the pattern of TMS IX #3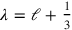 and an “extended width”
and an “extended width”
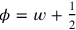 , and adding (according to the “Akkadian method”)
, and adding (according to the “Akkadian method”)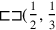 ) which is lacking in the corner where 2 and 3 are “inscribed,” we would have reduced the problem to
) which is lacking in the corner where 2 and 3 are “inscribed,” we would have reduced the problem to
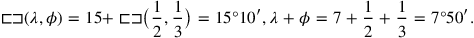
|
However, the present text does not proceed like that—Old Babylonian
algebra was a flexible instrument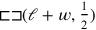 (represented by the number 3°30′) is brought physically to the place where length and width (provided with widths
(represented by the number 3°30′) is brought physically to the place where length and width (provided with widths
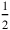 and
and
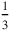 ) are to be found. In this way it becomes possible to “cut off” the rectangle
) are to be found. In this way it becomes possible to “cut off” the rectangle
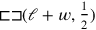 —as long as it was elsewhere that would make no sense. In bottom of Figure (4.2), the area that is eliminated is drawn shaded and black: the rest, in white, will be equal to 11°30′.
—as long as it was elsewhere that would make no sense. In bottom of Figure (4.2), the area that is eliminated is drawn shaded and black: the rest, in white, will be equal to 11°30′.
In this operation, it is obvious that the (shaded) half of the length that had been “joined” according to the statement has been eliminated. However, more than the (equally shaded) third of the width has disappeared. How much more precisely?
It would be easy to subtract
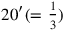 from
from
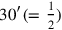 , but that may not have been deemed sufficiently informative.4 In any case, the text introduces a detour by the phrase “Do not go beyond!” (the same verb as in the “subtraction by comparison”). A rectangle
, but that may not have been deemed sufficiently informative.4 In any case, the text introduces a detour by the phrase “Do not go beyond!” (the same verb as in the “subtraction by comparison”). A rectangle
 (3,2) is constructed (perhaps one should imagine it in the corner where 2 and 3 are “inscribed” in Figure 4.2; in any case Figure 4.3 shows the situation). Without further argument it is seen that the half (three small squares) exceeds the third (two small squares) by one of six small squares, that is, by a sixth—another case of reasoning by “false position.”
(3,2) is constructed (perhaps one should imagine it in the corner where 2 and 3 are “inscribed” in Figure 4.2; in any case Figure 4.3 shows the situation). Without further argument it is seen that the half (three small squares) exceeds the third (two small squares) by one of six small squares, that is, by a sixth—another case of reasoning by “false position.”
We thus know that, in addition to the third of the width, we have eliminated a piece
 (w,10′) (drawn in black); if
(w,10′) (drawn in black); if
 , we therefore have
, we therefore have
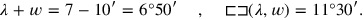
|
Once more we therefore have a rectangle of which we know the area and the sum of length and width. The procedure is the same as in the final part of TMS IX #3
In the end, the final addition of the side of the square precedes the subtraction, as in TMS IX #3. Once more, indeed, it is not the same piece that is involved in the two operations; there is therefore no need to make it available before it is added.
VAT 7532
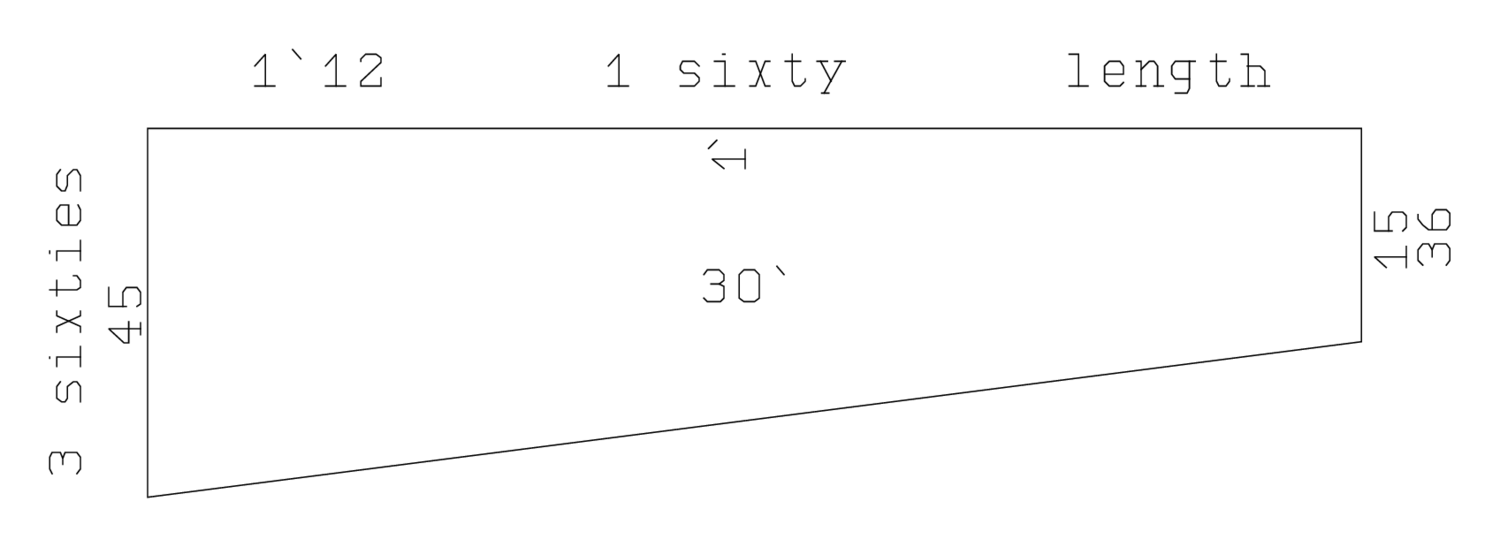
Fig. 4.5: The diagram of VAT 7532. The “upper width” is to the left.
Obv.
1A trapezium. I have cut off a reed.
21 sixty (along) the length I have gone. The 6th part
3broke off for me: 1‵12 to the length I have made follow.
4I turned back. The 3rd part and
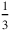 kùš broke off for me:
kùš broke off for me:
53 sixty (along) the upper width I have gone.
6With that which broke off for me I enlarged it:
736 (along) the width I went. 1 bùr
8You, by your proceeding, (for) the reed which you do not know,
91 may you posit. Its 6th part make break off, 50′ you leave.
10igi 50′ detach, 1°12′ to 1 sixty raise:
111‵12 to
 1‵12
1‵12
 join: 2‵24 the false length it gives you.
join: 2‵24 the false length it gives you.
12(For) the reed which you do not know, 1 may you posit. Its 3rd part make break off,
1340′ to 3 sixty of the upper width raise:
142‵ it gives you. 2‵ and 36 the lower width heap,
152‵36 to 2‵24 the false length raise,
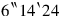 the false surface.
the false surface.
16The surface to 2 repeat,
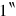 to
to
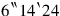 raise
raise
17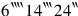 it gives you. And
it gives you. And
 kùš which broke off
kùš which broke off
18to 3 sixty raise: 5 to 2‵24, the false length,
19raise: 12‵.
 of 12‵ break, 6‵ make encounter,
of 12‵ break, 6‵ make encounter,
Rev.
1 to
to
 join,
join,
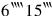 it gives you.
it gives you.
2By
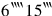 ,
,
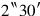 is equal. 6‵ which you have left
is equal. 6‵ which you have left
3to
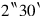 join,
join,
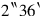 it gives you. igi
it gives you. igi
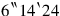 ,
,
4the false surface, I do not know. What to
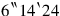
5may I posit which
 gives me? 25′ posit.
gives me? 25′ posit.
6Since the 6th part broke off before,
76 inscribe: 1 make go away
8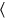 igi 5 detach, 12′ to 25 raise, 5′ it gives you
igi 5 detach, 12′ to 25 raise, 5′ it gives you
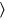 . 5′ to 25′ join:
. 5′ to 25′ join:
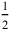 nindan, the head of the reed it gives you.
nindan, the head of the reed it gives you.
This problem nindan) corresponds indeed to a measuring unit often used in practical life and called precisely a “reed” (gi in Sumerian). One may also imagine that such reeds would easily break. Finally, the use of the numeral “sixty”
nindan) corresponds indeed to a measuring unit often used in practical life and called precisely a “reed” (gi in Sumerian). One may also imagine that such reeds would easily break. Finally, the use of the numeral “sixty”
Everything else, however—that is, that the area of the field is known before it is measured, and also the ways to indicate the measures of the pieces that break off from the reed—shows which
ruses the Old Babylonian school masters had to make use of in order to produce second-degree problems
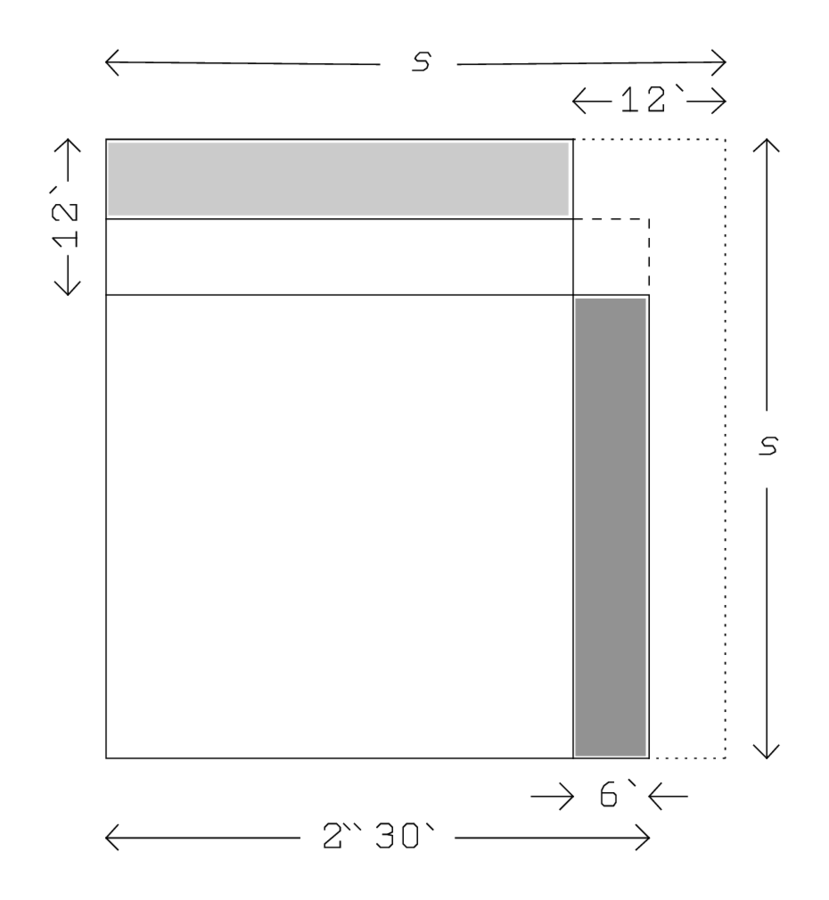
For once, Figure 4.5 reproduces a diagram that is traced on the tablet itself. In general, as also here, diagrams are only drawn on the tablets
We thus undertake to measure the trapezium by means of a reed of unknown length
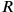 . We manage to measure 1‵ reed lengths along the length of the trapezium before the reed loses a sixth of its length and is reduced to
. We manage to measure 1‵ reed lengths along the length of the trapezium before the reed loses a sixth of its length and is reduced to
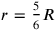 . What remains of the length turns out to be 1‵12
. What remains of the length turns out to be 1‵12
 (lines Obv. 2–3).
(lines Obv. 2–3).
Then the reed breaks for the second time. According to lines Obv. 4 and 5, the measure of the “upper width” (to the left)6 is 3‵
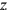 , where
, where
 kùš is the length of the reed after this second reduction.
kùš is the length of the reed after this second reduction.
The piece that broke off last is put back into place, and the “(lower) width” (evidently to the right) is paced out (line Obv. 7) as 36 r. Finally we learn that the area of the field is 1 bùr = 30‵ sar (1 sar = 1 nindan2), see page
Lines Obv. 9–11 determine the length in units
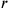 by means of a false position
by means of a false position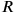 had been equal to 1, then
had been equal to 1, then
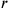 would have been 50′; conversely,
would have been 50′; conversely,
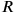 must correspond to
must correspond to
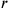 multiplied by igi
multiplied by igi
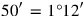 . 1‵ steps of
. 1‵ steps of
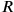 thus correspond to
thus correspond to
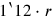 , and the complete length will be
, and the complete length will be

|
The text speaks of 2‵24 as the “false length,” that is, the length expressed in units
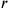 .
.
Another false position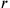 of the reed once shortened, and deducts that what remains after the loss of
of the reed once shortened, and deducts that what remains after the loss of
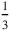
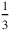 kùš, the false upper width (the upper width measured in units
kùš, the false upper width (the upper width measured in units
 ) is thus 40′ times 3 sixties, that is,
) is thus 40′ times 3 sixties, that is,
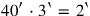 . In other words, the upper width measures 2‵
. In other words, the upper width measures 2‵
 —still leaving aside the missing piece of
—still leaving aside the missing piece of
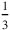 kùš.
kùš.
Since line Obv. 7 indicates that the false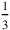 kùš—the three sides that will allow us to determine the area of the trapezium in units
kùš—the three sides that will allow us to determine the area of the trapezium in units
 .
.
Yet the text does not calculate this area: The surface to 2 repeat. Instead it doubles the trapezium so as to form a rectangle (see the left part of Figure 4.6), and the lines Obv. 14–16 calculate the area of this rectangle (the “false surface”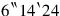 (in the implicit unit
(in the implicit unit
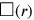 ).
).
If the reed had not lost an ulterior piece of
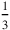 kùš, we might now have found the solution by means of a final false position similar to that of BM 13901 #10
kùš, we might now have found the solution by means of a final false position similar to that of BM 13901 #10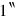 nindan2 (Obv. 16: The surface to 2 repeat,
nindan2 (Obv. 16: The surface to 2 repeat,
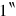 ). However, things are more complicated here. For each of the 3‵ steps made by the twice shortened reed a piece of
). However, things are more complicated here. For each of the 3‵ steps made by the twice shortened reed a piece of
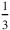 kùš is missing from our calculation, in total thus
kùš is missing from our calculation, in total thus
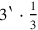 kùš = 1‵ kùš = 5 nindan (1 kùš =
kùš = 1‵ kùš = 5 nindan (1 kùš =
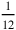 nindan): And
nindan): And
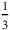 kùš which broke off to 3 sixty raise: 5 (Obv. 17–18). Therefore the area of the real field does not correspond to what we see to the left in Figure 4.6 but to that which remains after elimination of the shaded strip to the right. The area of this strip is
kùš which broke off to 3 sixty raise: 5 (Obv. 17–18). Therefore the area of the real field does not correspond to what we see to the left in Figure 4.6 but to that which remains after elimination of the shaded strip to the right. The area of this strip is
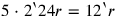 : 5 to 2‵24, the false length, raise: 12‵. The relation
: 5 to 2‵24, the false length, raise: 12‵. The relation

|
This non-normalized equation is solved in the usual way. First it is multiplied by
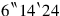 :
:
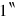 to
to
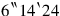 raise
raise
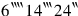 it gives you (Obv. 16–17). That leads to the normalized equation
it gives you (Obv. 16–17). That leads to the normalized equation
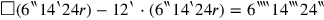
|
or, with
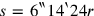 r as unknown,
r as unknown,
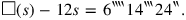
|
From here onward, the procedure coincides with that of BM 13901 #2
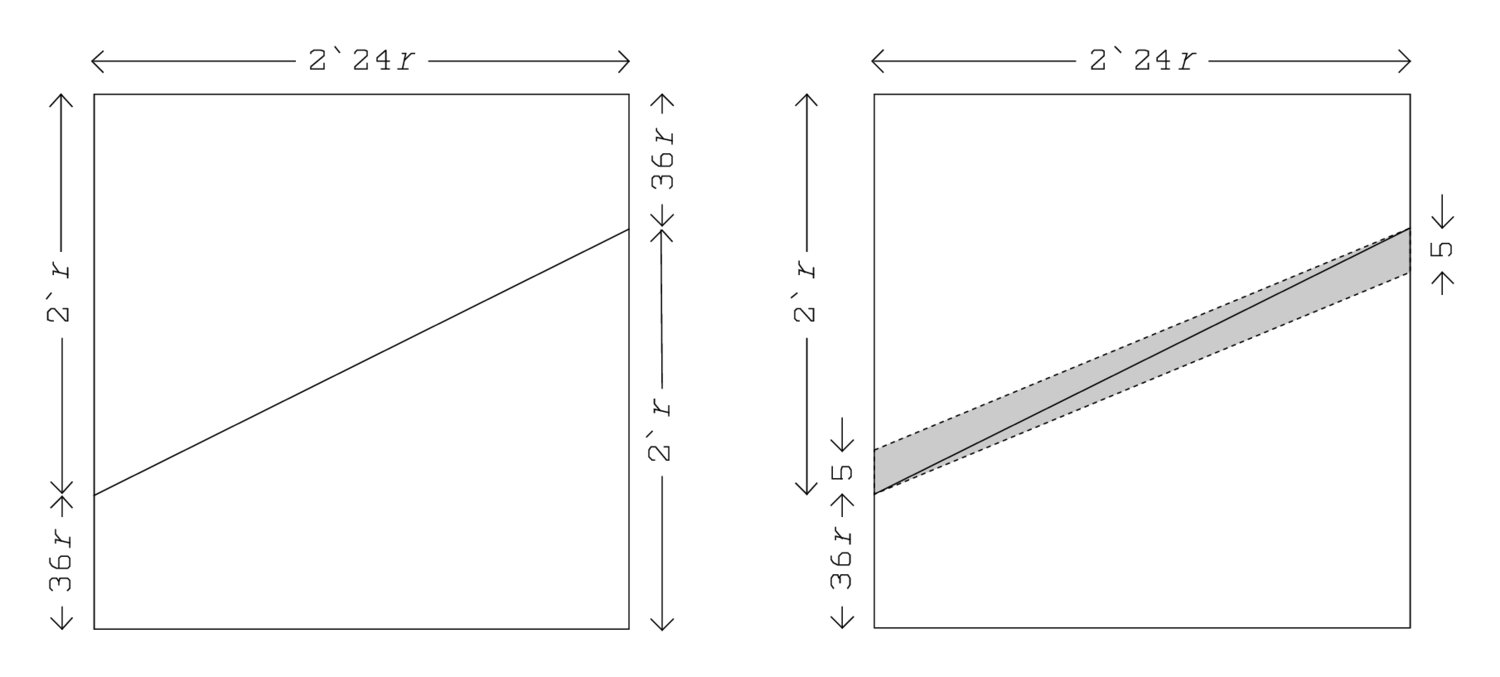
The area
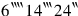 corresponds to the rectangle of (height)
corresponds to the rectangle of (height)
 and breadth
and breadth
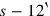 . Half of the excess of the height over the breadth is “broken” and repositioned as seen in the diagram: lightly shaded in the original positions, heavily shaded where it is moved to. The construction of the completing square is described with one of the synonyms
. Half of the excess of the height over the breadth is “broken” and repositioned as seen in the diagram: lightly shaded in the original positions, heavily shaded where it is moved to. The construction of the completing square is described with one of the synonyms
After the usual operations we find that
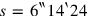
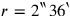 , and in line Rev. 5 that
, and in line Rev. 5 that
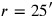 . We observe, however, that the “moiety” that was moved around is not put back into its original position, which would have reconstituted
. We observe, however, that the “moiety” that was moved around is not put back into its original position, which would have reconstituted
 in the vertical direction. Instead, the other “moiety,” originally left in place, is also moved, which allows a horizontal reconstitution
in the vertical direction. Instead, the other “moiety,” originally left in place, is also moved, which allows a horizontal reconstitution
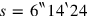
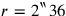 : 6‵ which you have left to 2‶30‵ join, 2‶36‵ it gives you.7
: 6‵ which you have left to 2‶30‵ join, 2‶36‵ it gives you.7
In the lines Rev. 6–8, the calculator introduces a third false position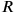 had been equal to 6, then
had been equal to 6, then
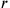 would be 5. The difference of 1 between
would be 5. The difference of 1 between
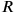 and
and
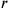 is
is
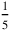 of
of
 or 12′ times
or 12′ times
 . Now the true value of
. Now the true value of
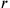 is 25′; in order to obtain
is 25′; in order to obtain
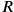 we must hence “join”
we must hence “join”
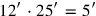 to it. Therefore
to it. Therefore
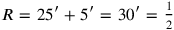 nindan.
nindan.
One might believe this problem type to be one of the absolute favorites of the Old Babylonian teachers of sophisticated mathematics. We know four variants of it differing in the choice of numerical parameters. However, they all belong on only two tablets sharing a number of terminological particularities—for instance, the use of the logogram
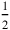 for the “moiety,” and the habit that results are “given,” not (for example) “seen” or “coming up.” Both tablets are certainly products of the same locality and local tradition (according to the orthography based in Uruk), and probably come from the same school or even the same hand. A simpler variant with a rectangular field, however, is found in an earlier text of northern origin, and also in a text belonging together with the trapezium variants; if not the favorite, the broken reed was probably a favorite.
for the “moiety,” and the habit that results are “given,” not (for example) “seen” or “coming up.” Both tablets are certainly products of the same locality and local tradition (according to the orthography based in Uruk), and probably come from the same school or even the same hand. A simpler variant with a rectangular field, however, is found in an earlier text of northern origin, and also in a text belonging together with the trapezium variants; if not the favorite, the broken reed was probably a favorite.
TMS XIII
As TMS VII #2
12 gur 2 pi 5 bán of oil I have bought. From the buying of 1 shekel of silver,
24 silà, each (shekel), of oil I have cut away.
3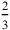 mina of silver as profit I have seen. Corresponding to what
mina of silver as profit I have seen. Corresponding to what
4have I bought and corresponding to what have I sold?
5You, 4 silà of oil posit and 40, (of the order of the) mina, the profit posit.
6igi 40 detach,
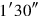 you see,
you see,
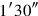 to 4 raise, 6′ you see.
to 4 raise, 6′ you see.
76′ to 12‵50, the oil, raise, 1‵17 you see.
8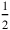 of 4 break, 2 you see, 2 make hold, 4 you see.
of 4 break, 2 you see, 2 make hold, 4 you see.
94 to 1‵17 join, 1‵21 you see. What is equal? 9 is equal.
109 the counterpart posit.
 of 4 which you have cut away break, 2 you see.
of 4 which you have cut away break, 2 you see.
112 to the 1st 9 join, 11 you see; from the 2nd tear out,
127 you see. 11 silà each (shekel) you have bought, 7 silà you have sold.
13Silver corresponding to what? What to 11 ¿silà? may I posit
14which 12‵50 of oil gives me? 1‵10 posit, 1 mina 10 shekel of silver.
15By 7 silà each (shekel) which you sell of oil,
16that of 40 of silver corresponding to what? 40 to 7 raise,
174‵40 you see, 4‵40 of oil.
This is another problem gur 2 pi 5 bán (= 12‵50 sìla) of fine oil (probably sesame oil). We are not told how much he paid, but the text informs us that from the quantity of oil which he has bought for one shekel (a) he has cut away 4 sìla, selling what was left (
gur 2 pi 5 bán (= 12‵50 sìla) of fine oil (probably sesame oil). We are not told how much he paid, but the text informs us that from the quantity of oil which he has bought for one shekel (a) he has cut away 4 sìla, selling what was left (
 ) for 1 shekel;
) for 1 shekel;
 and
and
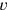 are thus the reciprocals of the two prices—we may speak of them as “rates” of purchase and sale. Moreover, the total profit
are thus the reciprocals of the two prices—we may speak of them as “rates” of purchase and sale. Moreover, the total profit
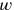 amounts to
amounts to
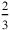 mina = 40 shekel of silver. For us, familiar with algebraic letter symbolism, it is easy to see that the total purchase price (the investment) must be
mina = 40 shekel of silver. For us, familiar with algebraic letter symbolism, it is easy to see that the total purchase price (the investment) must be
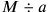 , the total sales price
, the total sales price
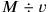 , and the profit in consequence
, and the profit in consequence
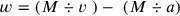 . Multiplying by
. Multiplying by
 we thus get the equation
we thus get the equation
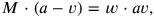
|
and since
 , the system
, the system
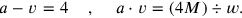
|
This system—of the same type as the one proposed in YBC 6967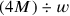 and not, as they actually do,
and not, as they actually do,
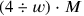 .
.
The cue to their method turns up towards the end of the text. Here the text first finds the total investment and next the profit in oil (4‵40 sìla). These calculations do not constitute a proof since these magnitudes are not among the data of the problem. Nor are they asked for, however. They must be of interest because they have played a role in the finding of the solution.
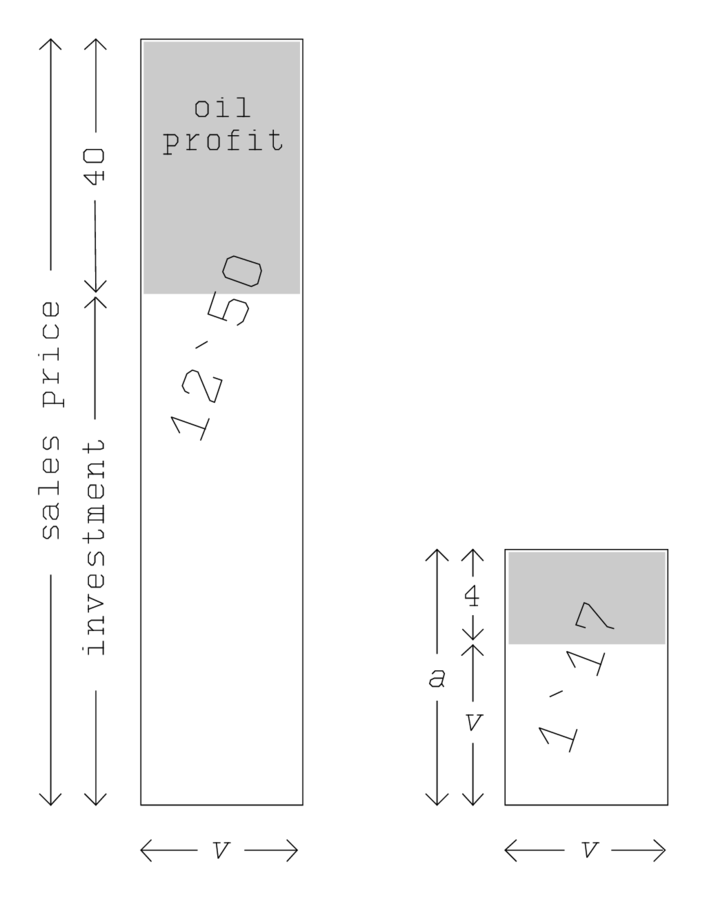
Figure 4.8 shows a possible and in its principles plausible interpretation. The total quantity of oil is represented by a rectangle, whose height corresponds to the total sales price in shekel, and whose
breadth is the “sales rate”
 (sìla per shekel). The total sales price can be divided into profit (40 shekel) and investment (purchase price), and the quantity of oil similarly into the oil profit and the quantity whose sale returns the investment.
(sìla per shekel). The total sales price can be divided into profit (40 shekel) and investment (purchase price), and the quantity of oil similarly into the oil profit and the quantity whose sale returns the investment.
The ratio between the latter two quantities must coincide with that into which the quantity bought for one shekel was divided—that is, the ratio between 4 sìla and that which is sold for 1 shekel (thus
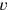 ).
).
Modifying the vertical scale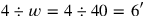 , the investment will be reduced to
, the investment will be reduced to
 , and the area to
, and the area to
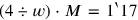 . In this way we obtain the rectangle to the right, for which we know the area (
. In this way we obtain the rectangle to the right, for which we know the area (
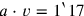 ) and the difference between the sides (
) and the difference between the sides (
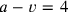 ), exactly as we should. Moreover, we follow the text in the order of operations, and the oil profit as well as the investment play a role.
), exactly as we should. Moreover, we follow the text in the order of operations, and the oil profit as well as the investment play a role.
On the whole, the final part of the procedure follows the model of YBC 6967 which we have “made hold” in line 8,
which we have “made hold” in line 8,
 is “broken”
is “broken”
In YBC 6967, the igûm-igibûm problem (page
BM 13901 #12
Obv. II
27The surfaces of my two confrontations I have heaped:
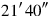 .
.
28My confrontations I have made hold: 10′.
29The moiety of
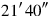 you break:
you break:
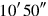 and
and
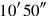 you make hold,
you make hold,
30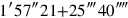 8 is it. 10′ and 10′ you make hold,
8 is it. 10′ and 10′ you make hold,
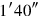
31inside
 you tear out: by
you tear out: by
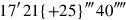 ,
,
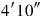 is equal.
is equal.
32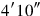 to one
to one
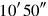 you join: by 15′, 30′ is equal.
you join: by 15′, 30′ is equal.
3330′ the first confrontation.
34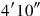 inside the second
inside the second
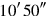 you tear out: by
you tear out: by
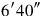 , 20′ is equal.
, 20′ is equal.
3520′ the second confrontation.
With this problem we leave the domain of fake practical life and return to the geometry of measured geometrical magnitudes. However, the problem we are going to approach may confront us with a possibly even more striking case of representation
This problem comes from the collection of problems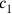 and
and
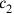 (see Figure 4.9):
(see Figure 4.9):
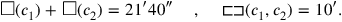
|
Fig. 4.9: The two squares and the rectangle of BM 13901 #12.
The problem could have been solved by means of the diagram shown in Figure 4.10, apparently already used to solve problem
Fig. 4.10: The diagram that corresponds to BM 13901 #8.
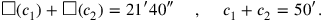
|
However, the author chooses a different method, showing thus the flexibility of the algebraic technique. He takes the two areas
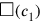 and
and
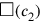 as sides of a rectangle, whose area can be found by making 10′ and 10′ “hold” (see Figure 4.10):
as sides of a rectangle, whose area can be found by making 10′ and 10′ “hold” (see Figure 4.10):
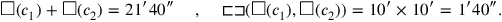
|
In spite of the geometric character of the operations the Babylonians were thus quite aware that the area of a rectangle whose sides are the squares
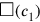 and
and
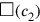 coincides with that of a square whose side is the rectangle
coincides with that of a square whose side is the rectangle
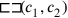 —which corresponds to our arithmetical rule
—which corresponds to our arithmetical rule
 .
.
We now have a rectangle for which we know the area and the sum of the two sides, as in the problems TMS IX #3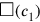 and
and
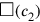 ; in order to know
; in order to know
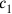 and
and
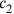 we must find out what “is equal by” them. The calculations can be followed on Figure 4.11.
we must find out what “is equal by” them. The calculations can be followed on Figure 4.11.
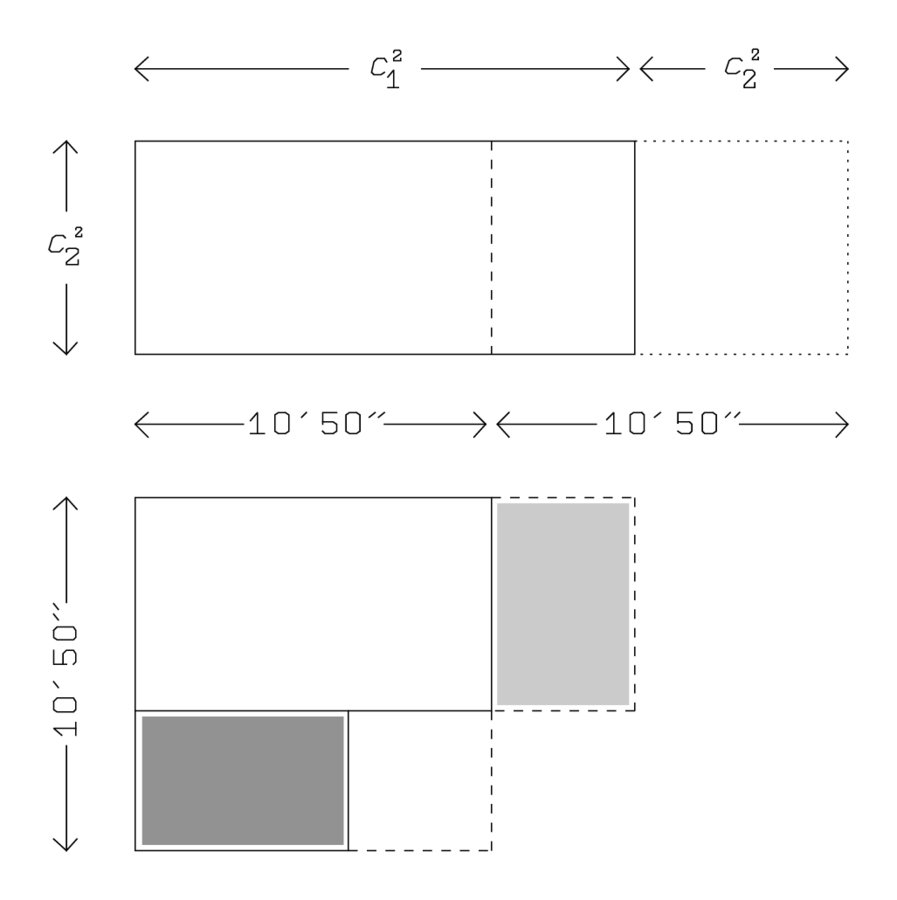
Fig. 4.11: The procedure used to solve the rectangle problem.
What is to be taken note of in this problem is hence that it represents areas by line segments and the square of an area by an area
BM 13901 #23
Rev. II
11About a surface, the four widths and the surface I have heaped,
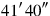 .
.
124, the four widths, you inscribe. igi 4 is 15′.
1315′ to
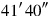 you raise:
you raise:
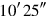 you inscribe.
you inscribe.
141, the projection, you join: by
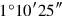 , 1°5′ is equal.
, 1°5′ is equal.
151, the projection, which you have joined, you tear out: 5′ to two
16you repeat: 10′, nindan, confronts itself.
Whereas the previous problem illustrates the “modern” aspect of Old Babylonian mathematics, the present one seems to illustrate its archaic side—even though they come from the same tablet.
This is no real contradiction. The present problem
The problem can thus be expressed in the following way:
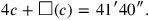
|
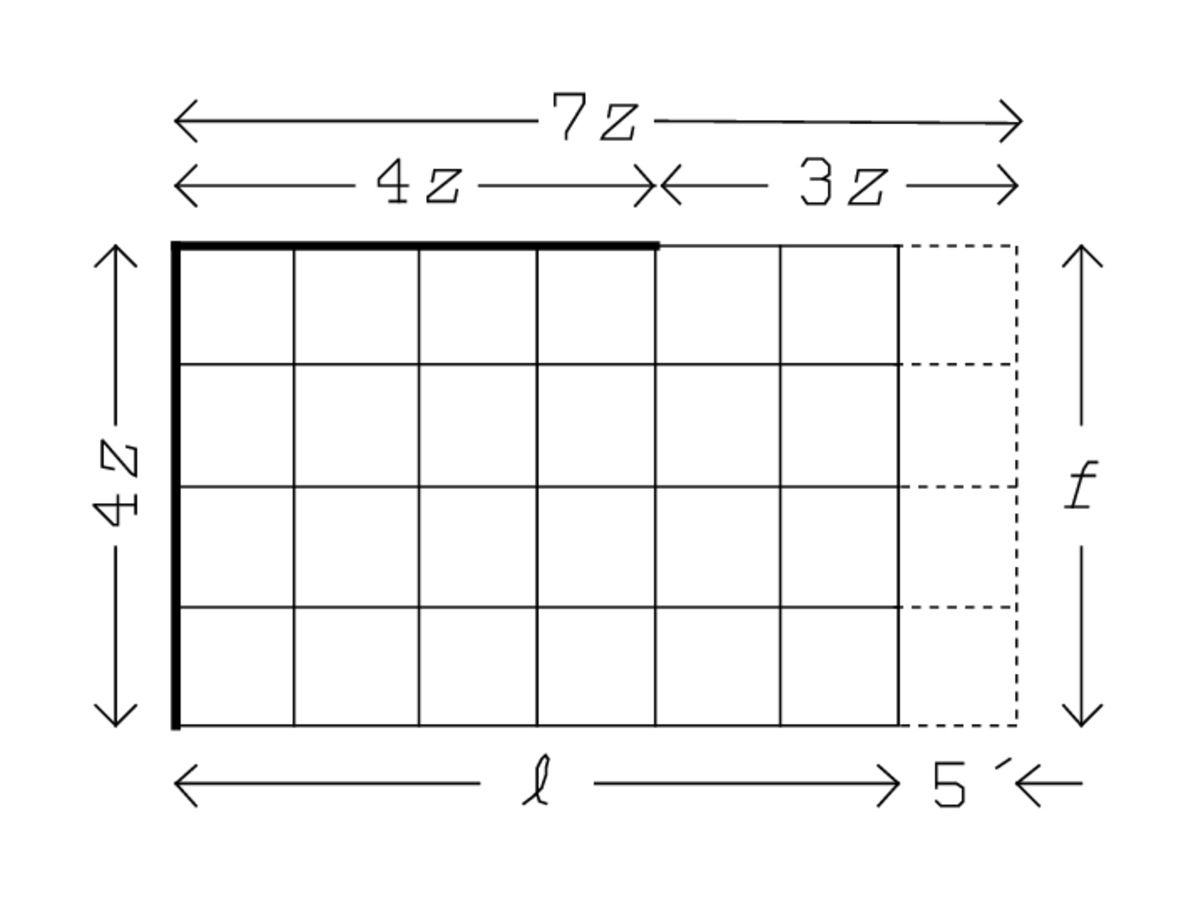
Figure 4.12 makes clear the procedure: 4c is represented by 4 rectangles
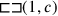 ; the total
; the total
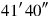 thus corresponds to the cross-shaped configuration where a “projection”
thus corresponds to the cross-shaped configuration where a “projection”
Lines 12–13 prescribe to cut out
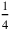 of the cross (demarcated by a dotted line) and the “joining” of a quadratic complement
of the cross (demarcated by a dotted line) and the “joining” of a quadratic complement
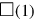 to the gnomon that results. There is no need to “make hold,” the sides of the complement are already there in the right position. But it is worthwhile to notice that it is the “projection” itself that is “joined”: it is hence no mere number but a quadratic configuration identified by its side.
to the gnomon that results. There is no need to “make hold,” the sides of the complement are already there in the right position. But it is worthwhile to notice that it is the “projection” itself that is “joined”: it is hence no mere number but a quadratic configuration identified by its side.
The completion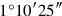 and thus side 1°5′. “Tearing out” the “projection”—now as a one dimensional
entity—we find 5′. Doubling this result, we get the side, which turns out to be 10′. Here again, the text avoids the usual term and does not speak of a “confrontation” as do the “modern” problems of the collection; instead it says that 10′ nindan “confronts itself.”
and thus side 1°5′. “Tearing out” the “projection”—now as a one dimensional
entity—we find 5′. Doubling this result, we get the side, which turns out to be 10′. Here again, the text avoids the usual term and does not speak of a “confrontation” as do the “modern” problems of the collection; instead it says that 10′ nindan “confronts itself.”
This method is so different from anything else in the total corpus that Neugebauer
The archaizing aspect, it should be added, does not dominate completely. Line 12, asking first for the “inscription” of 4 and stating afterwards its igi
TMS VIII #1
1The surface 10′. The 4th of the width to the width I have joined, to 3 I have gone … over
2the length 5′ went beyond. You, 4, of the fourth, as much as width posit. The fourth of 4 take, 1 you see.
31 to 3 go, 3 you see. 4 fourths of the width to 3 join, 7 you see.
47 as much as length posit. 5′ the going-beyond to the to-be-torn-out of the length posit. 7, of the length, to 4, ¿of the width?, raise,
528 you see. 28, of the surfaces, to 10′ the surface raise, 4°40′ you see.
65′, the to-be-torn-out of the length, to four, of the width, raise, 20′ you see.
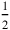 break, 10′ you see. 10′ make hold,
break, 10′ you see. 10′ make hold,
7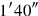 you see.
you see.
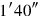 to 4°40′ join,
to 4°40′ join,
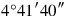 you see. What is equal? 2°10′ you see.
you see. What is equal? 2°10′ you see.
810′ ¿…? to 2°10′ join, 2°20′ you see. What to 28, of the surfaces, may I posit which 2°20′ gives me?
95′ posit. 5′ to 7 raise, 35′ you see. 5′, the to-be-torn-out of the length, from 35′ tear out,
1030′ you see, 30′ the length. 5′ the length to 4 of the width raise, 20′ you see, 20 the length (mistake for width).
In BM 13901 #12
Translated into symbols, the problem is the following;

|
(“to 3 I have gone” in line 1 means that the “joining” of
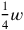 in line 1 is repeated thrice). The problem could have been solved in agreement with the methods used in TMS IX #3
in line 1 is repeated thrice). The problem could have been solved in agreement with the methods used in TMS IX #3
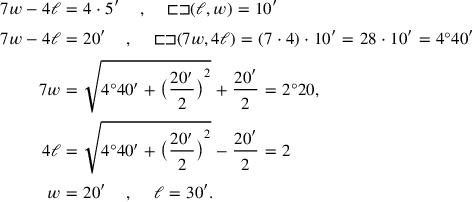
|
However , once again the calculator shows that he has several
strings on his bow, and that he can choose between them as he finds
convenient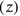 is
is
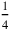 of the width (see Figure 4.13). In that way, the width will equal 4, understood as 4
of the width (see Figure 4.13). In that way, the width will equal 4, understood as 4
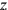 (You, 4, of the fourth, as much as width posit), and
the length prolonged by 5′ will be equal to 7, understood as 7z (7 as much as length posit). Line 4 finds that the rectangle with sides 7
(You, 4, of the fourth, as much as width posit), and
the length prolonged by 5′ will be equal to 7, understood as 7z (7 as much as length posit). Line 4 finds that the rectangle with sides 7
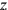 and 4
and 4
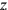 —in other words, the initial rectangle prolonged by 5′—consists of
—in other words, the initial rectangle prolonged by 5′—consists of
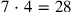 small squares
small squares
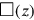 .11 These 28 squares exceed the area 10′ by a certain number of sides (
.11 These 28 squares exceed the area 10′ by a certain number of sides (
 ), the determination of which is postponed until later. As usual, indeed, the non-normalized problem
), the determination of which is postponed until later. As usual, indeed, the non-normalized problem
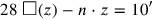
|
is transformed into
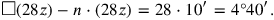
|
Line 6 finds
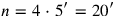 , and from here onward everything follows the routine, as can be seen on Figure 4.14: 28
, and from here onward everything follows the routine, as can be seen on Figure 4.14: 28
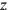 will be equal to 2°20′, and
will be equal to 2°20′, and
 hence to 5′.12 Therefore, the length
hence to 5′.12 Therefore, the length
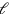 will be
will be
 , and the width
, and the width
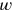
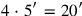 .
.
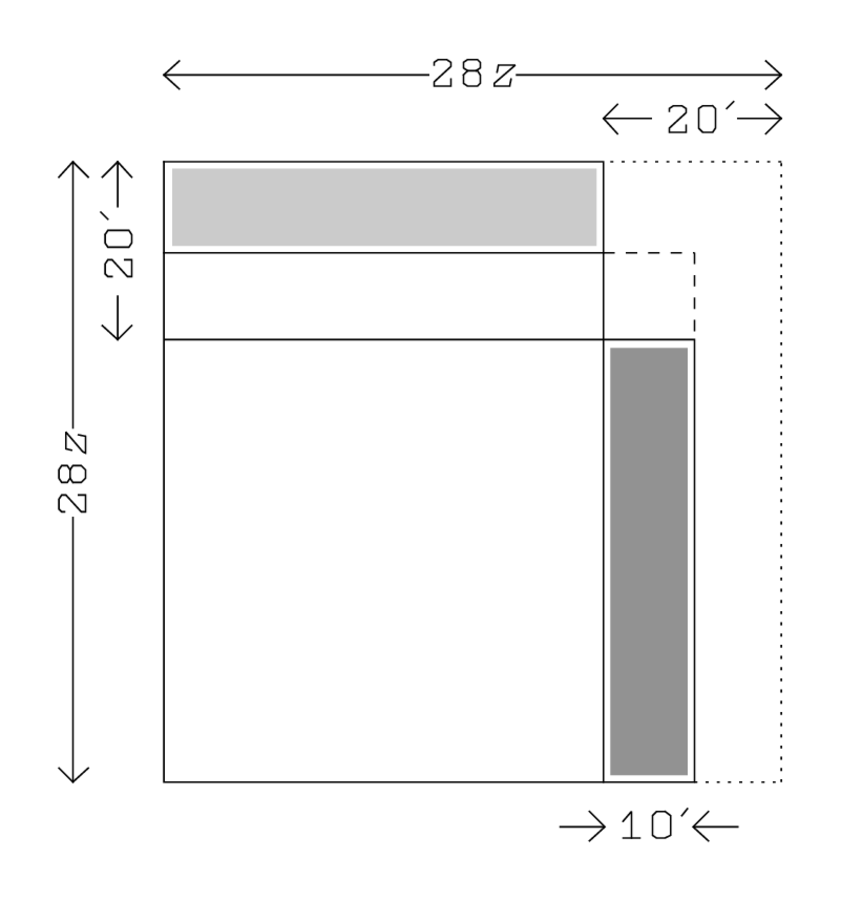
Fig. 4.14: Resolution of the normalized equation of TMS VIII #1.
YBC 6504 #4
Rev.
11So much as length over width goes beyond, made encounter, from inside the surface I have torn out:
12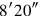 . 20′ the width, its length what?
. 20′ the width, its length what?
1320′ made encounter:
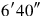 you posit.
you posit.
14 to
to
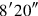 you join: 15′ you posit.
you join: 15′ you posit.
15By 15′, 30′ is equal. 30′, the length, you posit.
So far, everything we have looked at was mathematically correct,
apart from a few calculational and copying errors
The present text offers an example. Translated into symbols, the problem is the following:
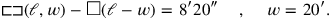
|
Astonishingly, the length is found as that which “is equal by”
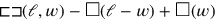 —that is, after a transformation and expressed in symbols, as
—that is, after a transformation and expressed in symbols, as
 .
.
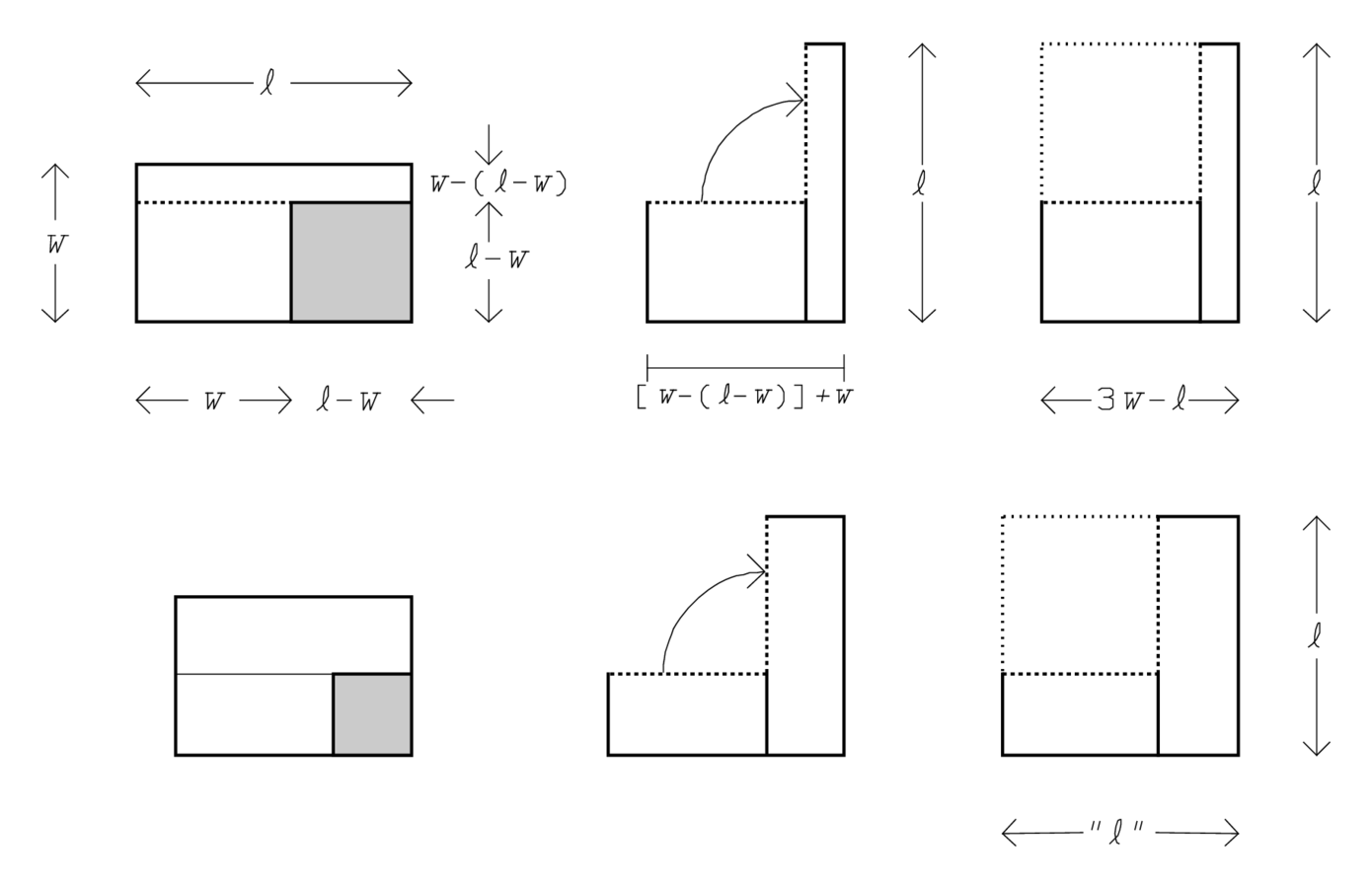
Fig. 4.15: The cut-and-paste operations of YBC 6504 #4.
The mistake seems difficult to explain, but inspection of the geometry of the argument reveals its origin (see Figure 4.15). On top the procedure is presented in distorted proportions; we see that the “joining” of
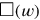 presupposes that the mutilated rectangle be cut along the dotted line and opened up as a pseudo-gnomon. It is clear that what results from the completion
presupposes that the mutilated rectangle be cut along the dotted line and opened up as a pseudo-gnomon. It is clear that what results from the completion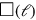 but instead—if one counts well—
but instead—if one counts well—
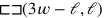 . Below we see the same thing, but now in the proportions of the actual problem, and now the mistake is no longer glaring. Here,
. Below we see the same thing, but now in the proportions of the actual problem, and now the mistake is no longer glaring. Here,
 and
and
 , and therefore
, and therefore
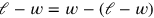 . In consequence the mutilated rectangle opens up as a true gnomon, and the completed figure corresponds to
. In consequence the mutilated rectangle opens up as a true gnomon, and the completed figure corresponds to
 —but only because
—but only because
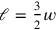 .
.
This mistake illustrates an important aspect of the “naive”
Footnotes
As the “to-be-joined” of page
We should observe that the half that appears here is treated as any other fraction, on an equal footing with the subsequent third. It is not a “moiety,” and the text finds it through multiplication by 30′, not by “breaking.”
Let us also take note that the half of the length and the third of the width are “joined” to the “surface,” not “heaped” together with it. A few other early texts share this characteristic. It seems that the surveyors thought in terms of “broad lines,” strips possessing a tacitly understood breadth of 1 length unit;
this practice is known from many pre-Modern surveying traditions, and agrees well with the Babylonian understanding of areas as “thick,” provided with an implicit height of 1 kùš (as inherent in the metrology of volumes, which coincides with that for areas—see page
The absence of this notion from the text should not prevent it from using it as a technical term of general validity.
Alternatively, the trick used by the text could be a leftover from the ways of surveyors not too familiar with the place-value system; or (a third possibility) the floating-point character of this system might make it preferable to avoid it in contexts where normal procedures for keeping track of orders of magnitude (whatever these normal procedures were) were not at hand.
It is not quite to be excluded that the text does not directly describe the construction but refers to the inscription twice of 3°25′ on a tablet for rough work, followed by the numerical product—cf. above, note 11, page
The position of the “upper” width to the left is a consequence of the new orientation of the cuneiform script (a counterclockwise rotation of 90°) mentioned in the box “Cuneiform writing.” On tablets, this rotation took place well before the Old Babylonian epoch, as a consequence of which one then wrote from left to right. But Old Babylonian scribes knew perfectly well that the true direction was vertically downwards—solemn inscriptions on stone (for example Hammurabi’s law) were still written in that way. For reading, scribes may well have turned their tablets 90° clockwise.
This distinction between two halves of which one is “left” is worth noticing as another proof of the geometric interpretation—it makes absolutely no sense unless understood spatially.
By error, line 30 of the text has
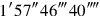 instead of
instead of
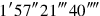 ; a partial product 25 has been inserted an extra time, which shows that the computation was made on a separate device where partial products would disappear from view once they had been inserted. This excludes writing on a clay surface and suggests instead some kind of reckoning board.
; a partial product 25 has been inserted an extra time, which shows that the computation was made on a separate device where partial products would disappear from view once they had been inserted. This excludes writing on a clay surface and suggests instead some kind of reckoning board.
The error is carried over in the following steps, but when the square root is taken it disappears. The root was thus known in advance.
In the original, the word is “surface” marked by a phonetic complement indicating the accusative. An accusative in this position is without parallel, and seems to allow no interpretation but the one given here.
For once, the determinate article corresponds to the Akkadian, namely to an expression which is only used to speak about an inseparable plurality (such as “the four quarters of the world” or “the seven mortal sins”).
The use of a “raising” multiplication shows that the calculator does not construct a new rectangle but bases his procedure on a subdivision of what is already at hand—see the discussion and dismissal of a possible alternative interpretation of the procedure of BM 13901 #10 in note 5, page
Line 10 speaks of this as 5′ the length—namely the side of the small square. Some other texts from Susa also speak of the side of a square as its “length.”