Drawings?
All the texts that were discussed above were illustrated by geometric drawings. However, only two of the tablets carried geometric diagrams, and in both cases these illustrated the problem statement, not the procedure.
Many aspects of the procedures are inexplicable in the traditional arithmetical interpretation but naturally explained in a geometrical reading. In consequence, some kind of geometry must have participated in the reasoning of the Babylonians. It is not very plausible, however, that the Babylonians made use of drawings quite like ours. On the contrary, many texts give us reasons to believe that they were satisfied with rudimentary structure diagrams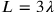 and
and
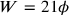 in TMS IX #3 (see page
in TMS IX #3 (see page 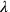 and
and
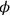 could be identified as sides of the “surface 2.”
could be identified as sides of the “surface 2.”
After all, that is no wonder. Whoever is familiar with the Old Babylonian techniques will need nothing but a rough sketch in order to follow the reasoning; there is not even any need to perform the divisions and displacements, the drawing of the rectangle alone allows one to grasp the procedure to be used. In the same way as we may perform a mental computation, making at most notes for one or two intermediate results, we may also become familiar with “mental geometry,” at most assisted by a rough diagram.
A fair number of field plans
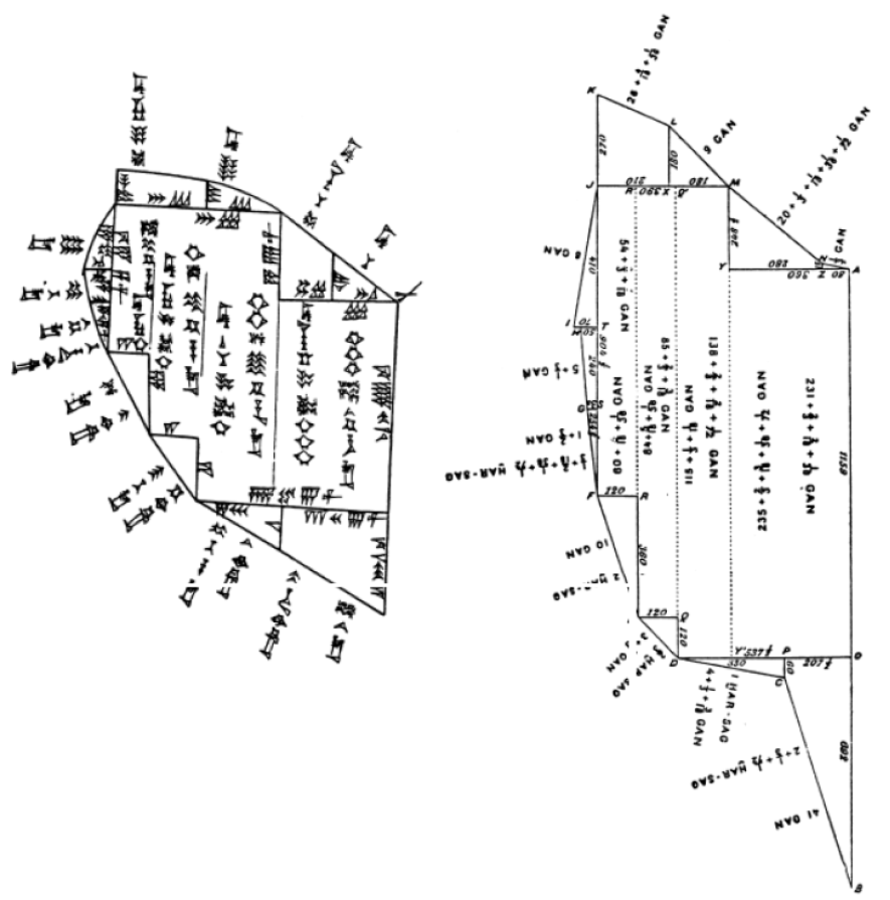
Fig. 6.1: A neo-Sumerian field plan (21st century bce), left as drawn on the tablet, right redrawn in correct proportions. After F. Thureau-Dangin, “Un cadastre chaldéen”. Revue d’Assyriologie 4 (1897–98), 13–27.
Practicing “mental geometry”
In the same way, dust or sand appears to have served in the first steps of learning the script. From this initial phase, we know the tablets on which are inscribed the models the students are supposed to have reproduced in order to learn the cuneiform characters. From the next phase we also have the clay tablets written by the students—but from the first phase the work of students has left no archaeological traces, which means that these will probably have been drawn in sand
Algebra?
Until now, for reasons of convenience and in agreement with the majority of historians of mathematics, we have spoken of an Old Babylonian “algebra” without settling the meaning
On our way, however, we have accumulated a number of observations that may help us form a reasoned opinion (at times hinting at the role these observations are going to play in the argument).
At first it must be said that the modern algebra to which the Old Babylonian technique might perhaps be assimilated is precisely a technique, namely the practice of equations. Nothing in the Old Babylonian texts allows us to assume that the Babylonians possessed the slightest hint of something like the algebraic theory which has developed from the sixteenth century (concerning the link between coefficients and roots, etc.)—nor a fortiori to equate what they did with what professional mathematicians today call algebra (group theory and everything building on or extending that domain). The algebra of today which we should think of is what is learned in school and expressed in equations.
We have seen above (page
But there is a difference. Today’s engineer operates on his equations: the magnitudes he moves from right to left, the coefficients he multiplies, the functions he integrates, etc.—all of these exist only as elements of the equation and have no other representation. The operations
With few exceptions (of which we have encountered none above) the Old Babylonian solutions are analytic
These shared characteristics—statements shaped as equations, analysis, homomorphic procedures—have induced many historians of mathematics to speak of a “Babylonian algebra” (seduced, certain critics have said during the last 40 years). But there is a further reason for this characterization, a reason that may be more decisive although it has mostly gone unnoticed.
Today’s equation algebra possesses a neutral “fundamental representation”
In this respect, the Babylonian technique is hence closer to modern equation algebra than is Greek analysis
Today’s equation algebra is thus a technique to find by means of the fiction that we have already found (analysis) followed by the manipulation of unknown magnitudes as if they were known—everything within a representation that is functionally empty (namely, the realm of abstract numbers). Replacing numbers with measurable geometric quantities we may say the same about the Old Babylonian technique—with a small reserve to which we shall return presently. If the modern technique is understood as an “algebra” in spite of its immense conceptual distance from group theory and its descendants, it seems reasonable to classify the Old Babylonian technique as we have encountered it in Chapters 2–4 under the same heading.
That does not mean that there are no differences; there are, and even important differences; but these are not of a kind that would normally be used to separate “algebra” from what is not algebra.
Apart from the representation . The problem which he constructs then states this value and requires (with a formulation that was in favor among the calculators of the Middle Ages but which is also present in TMS XVI
. The problem which he constructs then states this value and requires (with a formulation that was in favor among the calculators of the Middle Ages but which is also present in TMS XVI
This kind of algebra is very familiar today. It allows teachers and textbook authors to construct problems for school students for which they may be sure of the existence of a reasonable solution. The difference is that our artificial problems are supposed to train students in techniques that will later serve in “real-life” contexts.
What we do not know is the candor with which certain Old Babylonian texts speak of the value of magnitudes that in principle are supposed not to be known ,
,
 and
and
 of our algebra and the “segment
of our algebra and the “segment
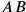 ” of our geometry. Since the texts represent the “teacher’s manual” (notwithstanding the “you” that pretends to address the student), we cannot exclude that the true oral exposition to students would instead make use of a finger pointing to the diagram (“this width here,” “that surface there”). Nor can we claim that things will really have occurred like that—we have no better window to the didactical practice of Old Babylonian mathematics than what is offered by TMS XVI #1 (page
” of our geometry. Since the texts represent the “teacher’s manual” (notwithstanding the “you” that pretends to address the student), we cannot exclude that the true oral exposition to students would instead make use of a finger pointing to the diagram (“this width here,” “that surface there”). Nor can we claim that things will really have occurred like that—we have no better window to the didactical practice of Old Babylonian mathematics than what is offered by TMS XVI #1 (page
Footnotes
The Greek word for the abacus, αβαξ, is borrowed from a Phoenician root from which come words for “dust” and “flying away.”
Only first-degree transformations like those of TMS XVI #1 and TMS IX #3 may be seen as constituting a partial exception; TMS XVI #1 is indeed an explanation of how operations directly on the words of the equation are to be understood in terms of the geometric representation. Once that had been understood, TMS IX #3 could probably operate directly on the level of words. But TMS XVI #1 is no problem solution, and in TMS IX #3 the first-degree transformation is subordinate to geometric operations.
See TMS XVI #2 line 16 and TMS VII #1 line 4 (below, pages
