Chapter structure
- 1.1 The challenge of a historical epistemology of space
- 1.2 Natural conditions of spatial cognition
- 1.3 Culturally shared mental models of space
- 1.4 Social control of space and metrization
- 1.5 Context-independence of mental models resulting from reflection
- 1.6 The expansion of experiential spaces over history
- 1.7 The decline of an autonomous concept of space
- 1.8 Concluding remarks
- Bibliography
- Footnotes
1.1 The challenge of a historical epistemology of space
In the history of Western epistemological thought, there is a long tradition of dividing human knowledge into a purely rational part, independent of any experience in the outer world, and an experiential part.1
Many aspects of spatial knowledge have traditionally been claimed to belong to the rational part. From the Pythagorean
The historical epistemology of space is similarly concerned with identifying the different sources of spatial knowledge. At the same time it is based on a thoroughly genetic, or developmental, view of cognition. According to this view, experiential knowledge participates in the construction of cognitive structures, which in turn constitute the basis for further experience. From this viewpoint a static separation between preformed structures of cognition and contingent experiences is impossible. Or rather, it is possible only in the snapshot image of a ‘cognitive subject’. If the idea of a foundation of human knowledge – and scientific knowledge in particular – is justified, then this foundation must consequently lie in the reconstruction and analysis of the processes that have led to this knowledge over the course of time. Kant’s
The developmental view on cognition is strongly suggested by results from different empirical disciplines. First and foremost, evolutionary biology teaches us that cognition is a function of the human organism, in particular the brain, and is therefore to be understood as a product of biological evolution. From studies in developmental psychology it has furthermore become clear that many fundamental cognitive structures are not present at the moment of a child’s birth, but are only gradually built up over the years in the long process of growing up. Finally, studies in the history of science and philosophy have revealed the historicity of fundamental concepts such as space, time, force, and matter, a historicity that became most obvious through the radical changes associated with the rise of the theories of relativity and the quantum in early twentieth-century physics.
Accordingly, we can distinguish three interwoven strands of development for which we can study the role of experience in the process of building up the perception and conception of space: 1) the phylogenetic
The phylogenesis
The ontogenesis
The historiogenesis of cognition is the subject matter of historical epistemology. Continuity of development is produced by external knowledge representations which serve the social reproduction of cognitive structures within a culture or their transfer between cultures. This reproduction relies on institutions
The historiogenetic strand is the one that will concern us in the following pages.9
It is closely interwoven with the other strands in two fundamental ways. First of all, in anthropogenesis
The second way historiogenesis is related to the two other strands of cognitive development is based on the fact that the species’ development, its phylogenesis
The intertwining of the ontogenetic
The recognition of this dialectic between individual thinking and shared knowledge
The identification of stages does not imply that the historical development of the forms of spatial thinking is a linear process. Although governed by entirely different mechanisms, this development actually shares some qualitative features with biological evolution, such as the following:
Unpredictability of future developments: Developmental processes are complex and interconnected, with the result that future developments are, as a rule, unpredictable at any time in history.
Dependency of later developments on earlier ones: Despite this indeterminacy, earlier developments produce the necessary preconditions for later ones.
Temporal directedness of overall development: This dependency of later developments on earlier ones explains aspects of the temporal order of development and makes it possible to define earlier and later stages of spatial thinking.
Asynchrony of development: The temporal directedness does not imply, however, that all development proceeds uniformly on a global scale: different stages coexist and there may even be local or temporal developments from a ‘later’ stage to an ‘earlier’ one.
In the following sections of this chapter we shall discuss six different aspects of the historical development of spatial knowledge.
The similar biological constitution of all humans and the fundamental similarities in their physical environments make it plausible to assume that there are structures of spatial cognition that do not vary between different cultures or over the course of history, but constitute the foundation for all cultural manifestations of spatial knowledge (section 1.2). While similar natural conditions hold for some animal species, humans possess unique social abilities to share knowledge, a fact that constitutes the basis for the cultural evolution of human spatial cognition, leading to elaborate cultural systems for orientation (section 1.3). The transformation of human societies from bands and tribes to city states and empires created new forms of the social control of space, involving techniques of surveying
1.2 Natural conditions of spatial cognition
In order to understand how human spatial thinking depends on the cultural conditions present at different times in history it is of fundamental importance first to identify spatial abilities and corresponding cognitive structures that are not products of human culture, and accordingly not subject to historical change. These may be termed the natural conditions of spatial cognition. Starting from such an identification we may then ask how historical and present-day cultural manifestations of spatial thinking relate to this universal
The natural conditions of spatial cognition have a double origin. First, there are biological predispositions of the human species which also involve a cognitive dimension. Second, there are features of the physical environment in which each individual grows up that are so fundamental that they are independent of culture. In the first case, it is the mechanisms of biological evolution by which experience enters the formation of cognitive structures, in the second it is each individual’s experience in ontogenesis
When trying to identify the natural conditions of spatial cognition we encounter a methodological problem. Cross-cultural studies help to identify aspects of spatial thinking that are human universals
To identify the natural conditions of spatial cognition the object of study must therefore be the spatial behavior of animals and humans (children and adults), and in particular of nonhuman primates
Besides
Besides humans, various species of animals exhibit sophisticated performance in spatial orientation.19
Nonhuman primates
We can summarize these findings as showing that the basic human cognitive mapping skills – similarly to object permanence skills – are not indicative of a peculiarity of human cognition but are part of its natural conditions:23
Overall, primates
Action and perception under control of the schemata of object permanence and the skills of cognitive mapping imply fundamental spatial structures which include the following:
Dichotomy of objects and spaces
Definiteness and exclusivity of place
Three-dimensionality of objects and spaces
Distinction of vertical direction
Continuity of object trajectories
Dichotomy of movable and unmovable objects
Focus on plane of movement: The space of movement (structured by a network of landmarks
Path-connectedness of plane of movement
Dependency of effort on path taken
What is the epistemic status of the natural conditions of spatial cognition and the described cognitive structures? As we have seen, these conditions are rooted in sensorimotor
It is important to note that the implied spatial structures described above are not in themselves an object of thinking. They allow for successful action, but there is no indication that the related spatial abilities imply any consciousness, that is, any reflection upon the schemata controlling the actions, and thereby go beyond the sensorimotor
In particular, there is no indication of symbol use
Besides the notion of schema of action we shall employ the concept of mental model
The sensorimotor
To describe a range of abilities in large-scale spatial orientation, we have employed the term cognitive mapping
Here the corresponding cognitive structures shall again be described in terms of mental models
1.3 Culturally shared mental models of space
If the natural conditions of human spatial cognition are similar to those of some animal species, as has been argued in the previous section, what accounts for the obvious distinction of human spatial abilities and thinking? Rather than attributing this distinction to some specifically human biological disposition for spatial cognition, the point shall be made here that the distinction can be explained as resulting from uniquely human abilities of social cognition. One argument against the existence of a specifically human module for spatial cognition is based on considerations of the necessary timescales for processes in biological evolution.37 We could adduce another argument if it could be shown that the specifity of human social cognition
The human ability of social cognition
Sharing knowledge crucially depends on what Piaget
Consequently, the crucial distinction between animal and human cognition is the emergence of a cumulatively evolving human culture, a thoroughly social phenomenon. For every ability of individual humans that may be argued to play a crucial role in the emergence of this culture, such as the ability to use and produce tools, or to understand conspecifics as intentional beings, or to understand symbols
An immediate consequence of the cultural evolution of human societies for spatial cognition is that the mental models
The sharing of mental models
Recent nonliterate societies show a wide variety of cultural systems for spatial orientation and communication.44
This cultural diversity is due not only to the self-referential dynamics of cultural evolution, but obviously also to the fact that these systems represent responses to the challenges of widely differing ecologies to which they are adapted. Nevertheless, there are common patterns that may be discerned. It may be observed, for instance, that toponyms
Two examples of recent nonliterate societies and their spatial language and practices are discussed in this book, the Eipo
Transmission through external knowledge representations. In contrast to sensorimotor
Cultural organization. This accumulation is accompanied by the cultural organization of knowledge – which, in fact, makes the mastery of the accumulated knowledge possible in the first place. Culturally shared large-scale space is spanned not only by landmarks
Dependence on the specific contexts of action. The spatial concepts structuring practical knowledge are, as a rule, not abstract or general but depend on the specific contexts of action. They are not applications of more general concepts in concrete situations but are rather conditioned by these situations.
Further, the way in which the concepts structuring practical thinking about large-scale space relate to more small-scale spaces remains largely undefined. As a consequence, metrization remains fragmentary. Distances
Locality. The shared mental models
To sum up, culturally shared mental models
1.4 Social control of space and metrization
An immediate consequence of the cultural evolution of human societies on spatial cognition, which was discussed in the previous section, is the development of elaborate practices of spatial orientation based on shared
The means for the social control of space depend on the respective form of social organization. In the case of small rural communities such as that of the Eipo
Historically, the earliest evidence for the systematic use of standardized measures for the social control of space stems from the so-called early civilizations. The growth in population of neolithic
A decisive strand in this bundle of developments was the emergence of new forms of the division of labor
As these mental activities are themselves dependent on material tools, the development of early civilizations went along with fundamental innovations in the means of external knowledge representation. This holds in particular for activities related to the social control of space such as architecture, urban planning, surveying
In this book the emergence and early development of the administrative control of space, and the related gradual metrization of space, is discussed using the example of Mesopotamia
The conservation of the size and shape of an object
The three-dimensionality of objects and spaces
The metric structure of space becomes more generalized through the application of the sexagesimal place value number system
Despite its novel degree of abstraction and its thorough metrization of area, the Babylonian surveyors’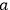 ,
,
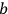 ,
,
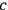 , and
, and
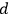 , which corresponds to an application of the formula
, which corresponds to an application of the formula
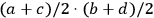 . Field areas are thus calculated on the basis of lengths without quantitatively accounting for the angles.55
. Field areas are thus calculated on the basis of lengths without quantitatively accounting for the angles.55
1.5 Context-independence of mental models resulting from reflection
The cultural developments of spatial thinking discussed in the preceding section show a basic trend towards cognitive structures that are less dependent on the specific practical contexts from which they originated. An example is the emerging practice of area determination by means of a multiplication of lengths within the sexagesimal place value system
Processes of reflective abstraction
One may distinguish two types of explorative knowledge, which may roughly be designated mathematical and philosophical. Mathematical explorative knowledge results from systematic reflection specifically on representations related to the use of instruments such as measuring rods
Among the most prominent historical settings in which the exploration of the cognitive tools of spatial thinking became productive are the intellectual traditions of ancient Greece
Among the later historical intellectual places which furthered deliberate and purposeful exploration of the implications of systems of knowledge representation were the Neoplatonic
All of the historical periods and places mentioned so far, in which the exploration of and reflection on representations of spatial knowledge took place, are more or less strongly related by ties of tradition: they all, in one way or another, relate back to the theoretical traditions of Greek antiquity. The example discussed in greater detail in this book, by contrast, presents a rare case of independent emergence of systematic reflections on spatial language
The spatial knowledge considered here can be described as theoretical knowledge. This kind of knowledge is largely conditioned by its means, that is, by the external knowledge representations from the exploration of which it emerges. It is handed down in text traditions, mostly in form of written language
The explorative reflection upon elementary structures of spatial thinking creates theoretical structures which preserve many of the spatial properties implied by sensorimotor
There is a striking difference between philosophical and mathematical explorative knowledge. While the former depends on individual decisions motivated within more encompassing knowledge systems and remained controversial throughout the history of philosophical thinking, the latter was, from early on, considered to present inevitable truths. The well-defined object of reflection of mathematical explorative knowledge, the first-order representations related to the use of instruments (figures drawn by means of a straight edge and compass
The reflection on the higher-order representations of Euclidean geometry
1.6 The expansion of experiential spaces over history
In the previous section we argued that reflection on the external representations of elementary and practical knowledge may lead to new and more general spatial concepts. In such cases of theoretical thinking, novelty arises from the structures inherent in the means of knowledge representation and tools for intellectual labor becoming explicit through being explored and through reflective abstraction
Starting with the first steps of ontogenesis
Another experiential space that has expanded over history is cosmological space. Cosmological space is the entire universe known, or assumed to exist, by a given society. Society transfers spatial concepts and knowledge acquired in terrestrial contexts to this space. It is, in particular, also the space of mythical
Microcosmic space, just like macrocosmic space, has been a target for projection of experiential knowledge from the mesocosmic realm, as the example of atomism
When considering the impact of the expansion of experiential spaces on spatial thinking, the objects of study are processes of concept formation fostered by the increase of experiential knowledge in the three realms described above: geographical
The knowledge discussed in these chapters is once again theoretical knowledge. Unlike the knowledge discussed in the previous section, it is theoretical knowledge resulting from systematic extensions of its experiential base. The accumulation of experiential knowledge takes place within institutions
The Earth has a spherical shape
Matter is nothing but empty space
The theoretical knowledge resulting from the expansion of experiential spaces has repercussions on different layers of knowledge. Global, geographical coordinates
Theoretical knowledge resulting from the expansion of experiential spaces also has repercussions on theoretical knowledge in general. The insight into the sphericity of the Earth
But theoretical knowledge resulting from the expansion of experiential spaces may also have an impact on meta-theoretical knowledge. This is strikingly demonstrated by the influence of Newton’s
[w]e can never have a presentation of there being no space, even though we are quite able to think of there being no objects encountered in it.
While space is thus a precondition of experience, rather than being derivable from experience, matter is not so, as Kant
1.7 The decline of an autonomous concept of space
In the previous sections we have argued that more and more general concepts of space emerged under more and more specific cultural conditions. In societies where centralized state administrations took over the social control of space, spatial measures became more standardized and integrated and eventually assumed general arithmetic properties (section 1.4). In societies where oral and written
The trend for increasingly general spatial concepts under ever more specific cultural conditions did not continue, however, within institutionalized
In twentieth-century physics these two aspects of generality became inapplicable to the developing concepts of space. While the aspiration of formulating fundamental concepts underlying all of physics has always remained a part of the agenda of theoretical physics, and unification is one of the major challenges of present-day theoretical work, there is no concept of space in twentieth-century physics that could consistently be applied to all fields of physics. The same applies to the concepts of time, matter and force. The most advanced concept of space in a well-established theory of modern physics is clearly that contained in the dynamic spacetime of general relativity
The autonomy of space, its independence from time, matter, force, and motion, which was a precondition for its universal homogeneity
The spatial knowledge under discussion in this context is a particular kind of theoretical knowledge, knowledge that develops only in a science that is highly structured in terms of disciplines and sub-disciplines
The boundaries between the areas shift in various ways over the course of time, resulting in knowledge integration and disintegration, but overarching theories remain a challenge. Thus, the theory of special relativity
The knowledge organized according to disciplines
1.8 Concluding remarks
This introduction started by raising questions about the epistemic status of spatial cognition. What is the relation between predetermined cognitive structures and experience? To what extent are the structures of spatial cognition universal
Naturally conditioned space is structured by elementary mental models
Culturally shared space
Administratively controlled space is represented by measuring tools, arithmetic and linguistic symbols
Mathematically reflected space generalizes metric structures by abstraction, using diagrams
Philosophically reflected space generalizes linguistically represented elementary structures by elevating them to the rank of principle and exploring the consequences.
Empirically and disciplinarily
A central concern of this chapter was to indicate in which ways these forms of space are genetically related. As we have seen, the occurrence of each new form of space depends on specific socio-cultural conditions. Its concrete realization, by contrast, does not solely depend on these conditions, but also on the cognitive structures it builds upon and on further experience. There is thus always both an aspect of construction and an aspect of experience in these spaces. Both aspects are closely intertwined, of course, because experience is always informed by cognitive structures already present in the mind, and, at the same time, it is experience that shapes the development of cognitive structures. One can thus say that there is no experience that is not structured by the mind, but there is also no mental structure that has not been shaped by experience. Our cognitive structures are the sediments of experience. But sedimentation is a historical process. This is why the understanding of the architecture of cognition requires the historical analysis of its genesis. The different forms of space represent not only successive historical stages, however. They also represent forms of thinking that are simultaneously present within single societies. Different forms of spatial knowledge are shared
Bibliography
Abbott, B. P. et al. (2016). Observation of Gravitational Waves from a Binary Black Hole Merger. Physical Review Letters 116:061102.
Asper, Markus (2009). The two cultures of mathematics in ancient Greece. In: The Oxford Handbook of the History of Mathematics. Ed. by Eleanor Robson and Jacqueline Stedall. Oxford: Oxford University Press, 107–132.
Bennett, Andrew T. D. (1996). Do Animals have Cognitive Maps? The Jounal of Experimental Biology 199:214–224.
Blum, Alexander and Dean Rickles, eds. (forthcoming). Quantum Gravity in the First Half of the Twentieth Century: A source book. Berlin: Edition Open Access.
Boesch, Christophe and Hedwig Boesch (1984). Mental Map in Wild Chimpanzees: An Analysis of Hammer Transports for Nut Cracking. Primates 25(2):160–170.
Burenhult, N., ed. (2008). Language and Landscape: Geographical Ontology in Cross-Linguistic Perspective. 30. Special Issue of Language Sciences 2–3. Elsevier.
Carnap, Rudolf (1922). Der Raum. Ein Beitrag zur Wissenschaftslehre. Berlin: Reuther & Reichard.
Chemla, Karine and Shuchun Guo, eds. (2004). Les neuf chapitres: Le classique mathématique de la Chine anciennne et ses commentaires. Paris: Dunod.
Cornell, Edward H. and C. Donald Heth (2004). Memories of travel: Dead reckoning within the cognitive map. In: Human Spatial Memory: Remembering where. Ed. by Gary L. Allen. Mahwah, NJ: Erlbaum, 191–215.
Damerow, Peter (1994). Vorüberlegungen zu einer historischen Epistemologie der Zahlbegriffsentwicklung. In: Der Prozeß der Geistesgeschichte. Studien zur ontogenetischen und historischen Entwicklung des Geistes. Ed. by Günter Dux and Ulrich Wenzel. Frankfurt a.M.: Suhrkamp, 248–322.
– (1996a). Abstraction and Representation. In: Abstraction and Representation: Essays on the Cultural Evolution of Thinking. Boston studies in the philosophy of science. Dordrecht/Boston/London: Kluwer, 371–381.
– (1996b). Abstraction and Representation. Essays on the Cultural Evolution of Thinking. Boston studies in the philosophy of science 175. Dordrecht/Boston/London: Kluwer.
– (1998). Prehistory and Cognitive Development. In: Piaget, Evolution, and Development. Ed. by Jonas Langer and Melanie Killen. Mahwa, NJ: Erlbaum, 247–269.
– (2000). How Can Discontinuities in Evolution Be Conceptualized? Culture and Psychology 6(2):155–160.
– (2001). Kannten die Babylonier den Satz des Pythagoras? Epistemologische Anmerkungen zur Natur der Babylonischen Mathematik. In: Changing Views on Ancient Near Eastern Mathematics. Ed. by Jens Høyrup and Peter Damerow. Berlin: Reimer, 219–310.
– (2007). The Material Culture of Calculation. A Theoretical Framework for a Historical Epistemology of the Concept of Number. In: Mathematisation and Demathematisation. Social, Philosophical and Educational Ramifications. Ed. by Uwe Gellert and Eva Jablonka. Rotterdam: Sense Publ., 19–56.
– (2012). The Origins of Writing and Arithmetic. In: The Globalization of Knowledge in History. Ed. by Jürgen Renn. Berlin: Edition Open Access, 153–173.
Damerow, Peter and Wolfgang Lefèvre (1996). Tools of Science. In: Abstraction and Representation. Essays on the Cultural Evolution of Thinking. Ed. by Peter Damerow. Dordrecht/Boston/London: Kluwer, 395–404.
De Risi, Vincenzo, ed. (2015). Mathematizing Space: The Objects of Geometry from Antiquity to the Early Modern Age. Cham: Springer.
Descartes, René (1644). Principia philosophiae. Amstelodami (Amsterdam): Elzevirium.
– (1984). Principles of Philosophy. Synthese Historical Library 24. Dordrecht: Reidel.
Dux, Günter (1992). Die Zeit in der Geschichte. Ihre Entwicklungslogik vom Mythos zur Weltzeit. Suhrkamp Taschenbuch Wissenschaft. Mit kulturvergleichenden Untersuchungen in Brasilien (J. Mensing), Indien (G. Dux / K. Kälble / J. Meßmer) und Deutschland (B. Kiesel). Frankfurt a.M.: Suhrkamp.
Ehlers, Jürgen (1986). On Limit Relations between, and Approximative Explanations of, Physical Theories. In: Logic, Methodology and Philosophy of Science VII. Ed. by Ruth Barcan Marcus, Georg J.W. Dorn, and Paul Weingartner. Amsterdam: North-Holland, 387–403.
Einstein, Albert and Adriaan D. Fokker (1914). Die Nordströmsche Gravitationstheorie vom Standpunkt des absoluten Differentialkalküls. Annalen der Physik 44:321–328.
Elias, Norbert (1988). Über die Zeit. Frankfurt a.M.: Suhrkamp.
Folkerts, Menso (1992). Mathematische Probleme im Corpus agrimensorum. In: Die römische Feldmeßkunst: Interdisziplinäre Beiträge zu ihrer Bedeutung für die Zivilisationsgeschichte Roms. Ed. by Okko Behrends and Luigi Capogrossi Colognesi. Göttingen: Vandenhoeck & Ruprecht, 311–336.
Foreman, Nigel, Margaret Arber, and Joe Savage (1984). Spatial Memory in Preschool Infants. Developmental Psychobiology 17(2):129–137.
Friedman, Michael (2001). Matter and Motion in the 'Metaphysical Foundations' and the First 'Critique': The Empirical Concept of Matter and the Categories. In: Kant and the sciences. Ed. by Eric Watkins. Oxford: Oxford University Press.
Gandz, Solomon (1929). The Origin of Angle-Geometry. ISIS 12(1929):452–481.
Gärling, Tommy, Anders Böök, and Erik Lindberg (1985). Adults' Memory Representations of the Spatial Properties of Their Everyday Physical Environment. In: The Development of Spatial Cognition. Ed. by Robert Cohen. Hillsdale: Erlbaum, 141–184.
Gent, Werner (1971). Die Philosophie des Raumes und der Zeit. Historische, kritische und analytische Untersuchungen, Bände I und II. Hildesheim: Georg Olms.
Gentner, Dedre and Albert Stevens, eds. (1983). Mental Models. Hillsdale: Erlbaum.
Gladwin, Thomas (1974). East is a Big Bird. Navigation and Logic on Puluwat Atoll. Cambridge, MA: Harvard University Press.
Gosztonyi, Alexander (1976). Der Raum. Geschichte seiner Probleme in Philosophie und Wissenschaften. Freiburg: Alber.
Guo, Shuchun, ed. (1993). Zhongguo ke xue ji shu dian ji tong hui: Shu xue juan yi 中國科學技術典籍通彙: 數學卷一. Zhengzhou: Henan jiaoyo chubanshe.
Hazen, Nancy L. (1983). Spatial Orientation. A Comparitive Aproach. In: Spatial Orientation: Theory, Research, and Application. Ed. by Herbert Pick and Linda Acredolo. New York: Plenum Press, 3–37.
Heeschen, Volker (1990). Ninye bún. Mythen, Erzählungen, Lieder und Märchen der Eipo (im zentralen Bergland von Irian Jaya, West-Neuguinea, Indonesien). Mensch, Kultur und Umwelt im Zentralen Bergland von West-Neuguinea 20. Berlin: Reimer.
Heth, C. Donald and Edward H. Cornell (1985). A Comparative Description of Representation and Processing During Search. In: Children’s Searching. The Development of Search Skill and Spatial Representation. Ed. by Henry M. Wellman. Hillsdale: Erlbaum, 215–249.
Høyrup, Jens (1994). In Measure, Number, and Weight: Studies in Mathematics and Culture. Albany: State University of New York Press.
– (2002). Length, Width, Surfaces: A Portrait of Old Babylonian Mathematics and Its Kins. New York: Springer.
Hume, David (2007). A Treatise of Human Nature: A Critical edition. Ed. by David Fate Norton and Mary J. Norton. Oxford: Clarendon Press.
Hyman, Malcolm and Jürgen Renn (2012). Survey: From Technology Transfer to the Origins of Science. In: The Globalization of Knowledge in History. Ed. by Jürgen Renn. Berlin: Edition Open Access, 75–104.
Jammer, Max (1954). Concepts of Space: The History of Theories of Space in Physics. Cambridge, MA: Harvard University Press.
Jeffares, Ben (2010). The Co-Evolution of Tools and Minds: Cognition and Material Culture in the Hominin Lineage. Phenomenology and the Cognitive Sciences 9:503–520.
Jungnickel, Christa and Russell MacCormmach (1986). Intellectual Mastery of Nature: Theoretical Physics from Ohm to Einstein. 2 Vols. Chicago: University of Chicago Press.
Kangshen, Shen, John N. Crossley, and Anthony W.-C. Lun, eds. (1999). The Nine Chapters on the Mathematical Art: Companion and Commentary. Oxford: Oxford University Press.
Kant, Immanuel (1996). Critique of Pure Reason: Unified edition; with all variants from the 1781 and 1787 editions. Indianapolis: Hackett.
– (1997). Metaphysische Anfangsgründe der Naturwissenschaft. Hamburg: Meiner.
– (1998). Kritik der reinen Vernunft (1. & 2. Aufl.) 505. Philosophische Bibliothek. Hamburg: Meiner.
Kitchin, Rob and Mark Blades (2002). The Cognition of Geographical Space. London: Tauris.
Koch, Gerd (1984). Maligdam. Ethnographische Notizen über einen Siedlungsbereich im oberen Eipomek-Tal, zentrales Bergland von Irian Jaya, West-Neuguinea, Indonesien. Mensch, Kultur und Umwelt im Zentralen Bergland von West-Neuguinea 15. Berlin: Reimer.
Koch, Gerd and Wulf Schiefenhövel (2009). Eipo (West-Neuguinea, Zentrales Hochland) - Neubau des sakralen Männerhauses in Munggona. DVD. Produktionsjahr: 1974, first published in 1979; IWF Bestellnummer/Bandzählung E 2475.
Langer, Jonas (2001). The mosaic evolution of cognitive and linguistic ontogeny. In: Language Acquisition and Conceptual Development. Ed. by Melissa Bowerman and Stephen C. Levinson. Cambridge: Cambridge University Press, 19–44.
Lefèvre, Wolfgang (1981). Rechensteine und Sprache. In: Rechenstein, Experiment, Sprache. Historische Fallstudien zur Entstehung der exakten Wissenschaften. Ed. by Peter Damerow and Wolfgang Lefèvre. Stuttgart: Klett-Cotta, 115–169.
– (1984). Die Wissenschaft in der geschichtlichen Entwicklung des Menschen. In: Kindlers Enzyklopädie: Der Mensch. Ed. by Norbert Loacker. Band 7. Zurich: Kindler, 295–328.
Levinson, Stephen C. and David Wilkins, eds. (2006). Grammars of Space. Cambridge: Cambridge University Press.
Lévi-Strauss, Claude (1955). Tristes tropiques. Paris: Plon.
Little John, J. (1963). Temne Space. Anthropological Quarterly 36(1):1–17.
Lorenz, Konrad (1977). Behind the Mirror. A Search for a Natural History of Human Knowledge. London: Methuen.
Lorenzen, Paul (1984). Elementargeometrie. Das Fundament der Analytischen Geometrie. Mannheim: Bibliographisches Institut.
Lyons, Henry (1927). Ancient Surveying Instruments. The Geographical Journal 69(2):132–139.
Marr, David (1982). Vision: A Computational Investigation in the Human Representation of Visual Information. San Francisco: Freeman.
Menzel, Emil W. (1973). Chimpanzee Spatial Memory Organization. Science 182(4115):943–945.
– (1987). Behavior as a Locationist Views it. In: Cognitive Processes and Spatial Orientation in Animal and Man. Volume I. Experimental Animal Psychology and Ethology. Ed. by Paul Ellen and Catherine Thinus-Blanc. Dordrecht: Martinus Nijhoff Publisher, 55–72.
Michel, Thomas (1983). Interdependenz von Wirtschaft und Umwelt in der Eipo-Kultur von Moknerkon. Bedingungen für Produktion und Reproduktion bei einer Dorfschaft im zentralen Bergland von Iran Jaya, West-Neugiunea, Indonesien. Mensch, Kultur und Umwelt im zentralen Bergland von West-Neuguinea 11. Berlin: Reimer.
Minsky, Marvin (1975). A Framework for Representing Knowledge. In: The Psychology of Computer Vision. Ed. by Patrick Henry Winston. New York: McGraw-Hill, 211–277.
Misner, Charles W., Kip S. Thorne, and John A. Wheeler (1973). Gravitation. New York: Freeman.
Neisser, Ulric (1976). Cognition and Reality: Principles and Implications of Cognitive Psychology. San Francisco: Freeman.
Neugebauer, Otto (1934). Vorlesungen ueber Geschichte der antiken mathematischen Wissenschaften: Band 1, Vorgriechische Mathematik. Berlin: Springer.
Newcombe, Nora S. and Janellen Huttenlocher (2003). Making Space. The Development of Spatial Representation and Reasoning. Cambridge, MA: MIT Press.
Normand, Emmanuelle and Christophe Boesch (2009). Sophisticated Euclidean Maps in Forest Chimpanzees. Animal Behaviour 30:1–7.
Norton, John D. (1992). Einstein, Nordström and the Early Demise of Scalar, Lorentz Covariant Theories of Gravitation. Archive for History of Exact Sciences 45:17–94.
Odling-Smee, F. John, Kevin N. Laland, and Marcus W. Feldman (2003). Niche Construction: The neglected process in evolution. Princeton, NJ: Princeton University Press.
Penrose, Roger (1989). The Emperor's New Mind: Concerning computers, minds, and the laws of physics. New York, NY: Oxford University Press.
Piaget, Jean (1959). The Construction of Reality in the Child. 5th print. The Basic Classics in Psychology. New York: Basic Books.
– (1970). Genetic Epistemology. New York: Columbia University Press.
– (1981). The Psychology of Intelligence. Totowa: Littelfield, Adams & Co.
– (1983). Biologie und Erkenntnis. Frankfurt am Main: Fischer.
Piaget, Jean and Bärbel Inhelder (1956). The Child's Conception of Space. London: Routledge & Kegan Paul.
Piaget, Jean, Bärbel Inhelder, and Alina Szeminska (1960). The Child's Conception of Geometry. Digital reprint 2007. Abingdon: Routledge.
Pick, Herbert and Linda Acredolo, eds. (1983). Spatial Orientation: Theory, Research, and Application. New York: Plenum Press.
Renn, Jürgen (2004). The Paradox of Scientific Progress. Notes on the Foundation of a Historical Theory of Knowledge. In: Research Report 2002-2003. Max Planck Institute for the History of Science, 21–49.
– (2005). The Relativity Revolution from the Perspective of Historical Epistemology. Isis 95(4):640–648.
– (2007). The Summit Almost Scaled: Max Abraham as a Pioneer of a Relativistic Theory of Gravitation. In: Gravitation in the Twilight of Classical Physics: Between Mechanics, Field Theory, and Astronomy. Ed. by Jürgen Renn and Matthias Schemmel. Dordrecht: Springer, 305–330.
Renn, Jürgen and Peter Damerow (2007). Mentale Modelle als kognitive Instrumente der Transformation von technischem Wissen. In: Übersetzung und Transformation. Ed. by Hartmut Böhme, Christof Rapp, and Wolfgang Rösler. Berlin: de Gruyter, 311–331.
Renn, Jürgen and John Stachel (2007). Hilbert's Foundation of Physics: From a Theory of Everything to a Constituent of General Relativity. In: Gravitation in the Twilight of Classical Physics: The Promise of Mathematics. Ed. by Jürgen Renn and Matthias Schemmel. Dordrecht: Springer, 857–973.
Robson, Eleanor (2008). Mathematics in Ancient Iraq. A Social History. Princeton: Princeton University Press.
Rovelli, Carlo (2008). Quantum Gravity. Cambridge: Cambridge University Press.
Savage-Rumbaugh, Sue (1998). Scientific Schizophrenia With Regard to the Language Act. In: Piaget, Evolution, and Development. Ed. by Jonas Langer and Melanie Killen. Mahwah, NJ: Erlbaum, 145–169.
Savage-Rumbaugh, Sue and William Fields (2000). Linguistic, Cultural and Cognitive Capacities of Bonobos (Pan Paniscus). Culture and Psychology 6:131–153.
Schemmel, Matthias (2016). Historical Epsitemology of Space: From Primate Cognition to Spacetime Physics. Cham: Springer.
Schick, Kathy D., Nicholas Toth, Gary Garufi, E. Sue Savage-Rumbaugh, Duane M. Rumbaugh, and Rose A. Sevcik (1999). Continuing Investigations into the Stone Tool-Making and Tool-Using Capabilities of Bonobo (Pan paniscus). Journal of Archaeological Science 26:821–832.
Schiefsky, Mark (2012). The Creation of Second-Order Knowledge in Ancient Greek Science as a Process in the Globalization of Knowledge. In: The Globalization of Knowledge in History. Ed. by Jürgen Renn. Berlin: Edition Open Access, 191–202.
Schurig, Volker (1976). Die Entstehung des Bewußtseins. Frankfurt a.M./New York: Campus.
Senft, Gunter, ed. (1997). Referring to Space: Studies in Austronesian and Papuan Languages. Oxford: Clarendon Press.
Siegel, Alexander W. and Sheldon H. White (1975). The Development of Spatial Representation of Large-Scale Environments. In: Advances in Child Development and Behavior. Ed. by Hayne W. Reese. New York: Academic Press.
Sigg, Hans and Alexander Stolba (1981). Home Range and Daily March in a Hamadryas Baboon Troop. Folio primatologica 36:40–75.
Stachel, John (2007). The Story of Newstein or: Is Gravity Just Another Pretty Force? In: Gravitation in the Twilight of Classical Physics: The Promise of Mathematics. Ed. by Jürgen Renn and Matthias Schemmel. Dordrecht: Springer, 1041–1078.
Stichweh, Rudolf (1984). Zur Entstehung des modernen Systems wissenschaftlicher Disziplinen: Physik in Deutschland 1740 - 1890. Frankfurt: Suhrkamp.
Tomasello, Michael (1999). The Cultural Origins of Human Cognition. Cambridge, MA: Harvard University Press.
Tomasello, Michael and Josep Call (1997). Primate Cognition. Oxford: Oxford University Press.
Tomasello, Michael, Ann Cale Kruger, and Hilary Horn Ratner (1993). Cultural learning. Behavioral and Brain Sciences 16(3):495–511.
Tuan, Yi-Fu (1975). Images and Mental Maps. Annals of the Association of American Geographers 65(2):205–214.
Vogel, Kurt, ed. (1968). Neun Bücher arithmetischer Technik: Ein chinesisches Rechenbuch für den praktischen Gebrauch aus der frühen Hanzeit (202 v. Chr. bis 9 n. Chr.) Braunschweig: Vieweg.
Vollmer, Gerhard (1994). Evolutionäre Erkenntnistheorie. Stuttgart: Hirzel.
Wallace, Ron (1989). Cognitive Mapping and the Origin of Language and Mind. Current Anthropology 30(4):518–526.
Wang, Ranxiao Frances and Elizabeth S. Spelke (2002). Human Spatial Representation: Insights from Animals. Trends in Cognitive Sciences 6:376–382.
Williams, Barbara J. and María del Carmen Jorge y Jorge (2008). Aztec Arithmetic Revisited: Land-Area Algorithms and Acolhua Congruence Arithmetic. Science 320(72):13–27.
Footnotes
This introductory chapter is based on the book: Matthias Schemmel, Historical Epistemology of Space: From Primate Cognition to Spacetime Physics, Springer, Cham, 2016.
For Plato, see, for instance, the discussion on geometry in Republic, 526c 9 – 527c 11. A prominent rationalistic treatment of space is found in René Descartes’ Principles of Philosophy, Part 2, in particular §§ 8–21, Descartes 1644, 37–44. For an English translation, see Descartes 1984, 42–49. An example from the early twentieth century of the division of spatial knowledge into an a priori and an experiential part is Carnap 1922, 62–67, who distinguishes formal, intuitive, and physical space, of which only the first is completely independent of experience; at the same time Carnap argues that the cognitive structure given by a topological space of infinitely many dimensions is the precondition for any kind of spatial experience. For a constructivist argument about the a priori nature of Euclidean space, see, for instance, Lorenzen (1984), who wants to show “how the Euclidean theorems can be proven in Plato’s sense solely from definitions and postulates (as fundamental constructions).” (“[…] wie die euklidischen Theoreme im Sinne Platons allein aus Definitionen und Postulaten (als Grundkonstruktionen) zu beweisen sind,” Lorenzen 1984, 15, English translation MS)
See Kant’s Transcendental Exposition of the Concept of Space in his Critique of Pure Reason, B 41–42, Kant 1998, 69–70.
See Lorenz 1977 for a classic work on evolutionary epistemology and Vollmer 1994 for a concise overview.
See Piaget 1970 and other works by Jean Piaget cited in this chapter.
‘Institutions’ are understood here in the most general sense as social patterns that structure and control collective actions.
Cf. Damerow 1996b, 371–381. Accounts on historical epistemology as the term is understood here include, among others, Renn 2004, Renn 2005, and Damerow 2007.
Related studies are Damerow 2007 concerning the concept of number, and Elias 1988 and Dux 1992 concerning the concept of time. For histories of concepts of space in science and philosophy over the long term, see Gent 1971, Jammer 1954, and Gosztonyi 1976.
See, for instance, Schurig 1976, in particular, 164–214 for a discussion of the coevolution of anatomy and culture in anthropogenesis. For a more recent account and further references to the literature, see Odling-Smee et.al. 2003, 239–281 who discuss coevolution from the perspective of niche construction.
Cf. Damerow 1994, 312. A common impulse against the idea of historical development of cognition is arguably rooted in the the well-meant attempt to avoid value judgements. But we may speak of development whenever change produces circumstances that serve as a necessary precondition for specific further changes. To deny historical development of cognition would mean to deny the dependency of cognition on its earlier forms and thus, ultimately, to deny its dependency on society and culture. But, as shall be argued below, this dependency is what distinguishes human cognition from animal intelligence. Its denial would mean to assume naively that any thought and insight was possible at any time in history. The outright identification of developmental approaches with value-judgements reveals an (often unconscious) ethnocentrism, since it uncritically presupposes that ‘our modern’ modes of thinking are more highly valued per se.
For a critical discussion of ‘nativist’ approaches, see, e.g., Tomasello 1999, 48–51.
For an explanation of cultural habitus, see Tomasello 1999, 78–81; for that of cultural learning, see Tomasello 1999, 61–70, who relates these human modes of learning to the conception of others as intentional beings and argues that its development begins around the ninth month.
For a more critical discussion of comparisons between animal and human spatial cognition, see Hazen 1983.
Piaget 1959, 97–101. For a definition of the concept of schema, see, for instance, Piaget 1983, 180–185. A different definition is given in Neisser 1976, 51–57. Below we will introduce the concept of mental model to describe relevant cognitive structures.
For a survey of the spatial abilities of nonhuman primates, see Tomasello and Call 1997.
See Kitchin and Blades 2002 for a recent account on cognitive maps which surveys a large part of this literature.
See various contributions in Pick, Herbert and Linda Acredolo 1983.
See Tomasello and Call 1997, 28–39 for a survey of the evidence for different primate species.
See Menzel 1973; Menzel 1987 discusses the interpretation of these findings in terms of cognitive mapping.
Tomasello and Call 1997, 55–56. There are further studies pointing to similarities in animal and human spatial cognition. Thus, Foreman, Arber, and Savage 1984, who carried out experiments with pre-school children in a so-called radial maze, an arrangement previously used in experiments on spatial abilities of animals, have pointed to remarkable similarities between pre-school children and well trained nonhumans in the performance of certain spatial tasks. This was interpreted to suggest a similarity of the role of visuospatial cues in the development and use of cognitive representations of space and the underlying processes across species.
Following Piaget, this is often referred to in the literature as ‘stage six abilities’.
See, e.g., Piaget 1981. See also Damerow 1998, 248.
They rely on what Piaget has called perceptional space in distinction to representational space, which is built up only at the preoperational and operational stages (Piaget and Inhelder 1956, 3–43). See, however, C. Boesch and H. Boesch (1984, 168–169) who interpret certain of their findings as evidence for concrete operational thinking in the spatial reasoning of nonhuman primates and suggest the existence of ‘Euclidean’ cognitive maps, relating to Piaget’s distinction between topological, projective, and Euclidean space; see also Normand and Boesch 2009.
It remains an open question to what extent the transfer of spatial abilities to novel and artificial contexts of action presupposes an understanding of the novel situation as involving a representation, e.g., when rhesus macaques using a joystick show that they are able to anticipate the path through a computer-simulated maze; see Tomasello and Call 1997, 51–54.
See the classical experiment by Piaget and Inhelder (1956, 209–246). For a critical discussion integrating recent empirical results, see Newcombe and Huttenlocher 2003, 118–125.
A possible counterexample of symbol use in spatial communication among bonobos is discussed in Savage-Rumbaugh 1998, 161–165, but does not seem conclusive.
We reserve the notion of concept to describe elements of knowledge structures that are somehow related to linguistic or otherwise symbolic representations, without implying, of course, that there is a one-to-one relation between concepts and words.
On the concept of mental model as understood here, see in particular Renn and Damerow 2007; see also various contributions in Gentner, Dedre and Albert Stevens 1983. The concept is akin to Marvin Minsky’s frames (Minsky 1975).
It is the functioning of the model – for instance, the way different perspectives are coordinated to make an object remain constant in size and shape under different views – that implies the three dimensionality. For a suggestion of how a three-dimensional cube and its transformations under different perspectives may be realized mentally without invoking a three-dimensional mental image, see Minsky 1975, 216–221, who uses coordinated frames. A more comprehensive discussion of three-dimensional vision is found in Marr 1982.
Objections against the imputed use of cognitive maps, in particular when simpler explanations of the spatial abilities are available, are raised, for instance, by Tuan 1975 and Bennett 1996. Recently, Wang and Spelke 2002 argued against the concept of cognitive map, emphasizing the human use of navigation techniques such as path integration, which are also found in insects and spiders and imply no more than the mental representation of one vector. It seems, however, that the presence of more ‘momentary’ and ‘egocentric’ representations in no way precludes the build-up of more enduring and comprehensive mental representations. On the relation of these two types of representations, see, for instance, Cornell and Heth 2004.
See Gärling et.al. 1985 for a detailed description of possible entities cognitive maps are made of.
On the specifically human ways of learning following from their ability to understand their conspecifics as intentional beings, see Tomasello et.al. 1993 and Tomasello 1999, 26–55.
Referring to results from neurology, developmental psychology, and archaeology, it has been speculated that the development of human language was closely related to the communication of cognitive maps (Wallace 1989).
Besides Tomasello and Call 1997, see, for instance, the discussion of cognitive abilities such as categorization as developing independent of language in Langer 2001 and reports on tool-making and tool-using abilities and linguistic capacities of bonobo individuals (Schick et.al. 1999, Savage-Rumbaugh and Fields 2000).
See, for instance, Damerow 2000 and Jeffares 2010.
Various examples are given in Levinson, Stephen C. and David Wilkins 2006.
Heeschen 1990. This appears to be a widespread means of organizing spatial knowledge; another example is the practices of the Ngatatjara who live in the Australian desert and use myths and ritualistic sequences of events to memorize and communicate the cultural knowledge about their habitat. A brief description is given in Heth and Cornell 1985, 232–235.
For the use of the star compass of the navigators of the Caroline Islands, see Gladwin 1974. See also Schemmel 2016 and the references provided there.
Koch and Schiefenhövel 2009 and Koch 1984, 49–54. See also Chapter 2.
Wulf Schiefenhövel, personal communication. See also Michel 1983. Other instances of the mythical control of space may be identified in the spatial practices and spatial thinking reported for the Bororo of the Brasilian central plateau – see the account of the socio-spatial structure of the village Kejara given by Lévi-Strauss (1955, 244–277) – and the Temne in northern Sierra Leone (Little John 1963).
See, e.g., Lyons 1927.
Consider, in particular, the Jiu zhang suan shu (Nine Chapters on Arithmetical Techniques), containing, among other things, problems on the calculation of field areas (Guo 1993, 79–213; for editions in European languages, see Vogel 1968; Kangshen, Shen, John N. Crossley, and Anthony W.-C. Lun 1999; and Chemla, Karine and Shuchun Guo 2004).
See also Damerow 2001; Høyrup 2002; and Robson 2008.
See Damerow 2012.
This method of determining areas was also used by the Roman agrimensores (Folkerts 1992, 324) and in demotic Egypt (Neugebauer 1934, 123). There is evidence that it may have also been used by Aztec surveyors (Williams and Carmen Jorge y Jorge 2008). On the origin of angle-geometry, see Gandz 1929.
See Damerow 1996a.
On the role of language as a means of knowledge representation in the emergence of theoretical mathematics, see Lefèvre 1981.
See Schiefsky 2012 for a concise discussion and references to the literature.
On the institutional background of the emergence of Greek mathematics, see Høyrup (1994, 9–15), who explicitly contrasts the Greek with the Babylonian case and argues for a close connection between the emergence of Greek mathematics and the contemporary philosophical discourse. See also Asper 2009.
On this point, see Chapter 6.
For an outline of the long-term transformation of the object of geometry from figures to second-order properties of figures, and eventually to space, which was a precondition for the formulation of non-Euclidean geometries, see De Risi 2015, 1–13. For a general discussion of first and higher order representations in the history of mathematics, see Damerow 1994.
On this point, see Chapter 7.
‘Knowledge acquisition’ or ‘knowledge production’, depending on whether one wishes to stress the objective or the constructive aspect of knowledge growth.
On Kant’s empirical concept of matter, see Friedman 2001.
Einstein, on p. xiv in his foreword to Max Jammer’s Concepts of Space (Jammer 1954, xi–xvi), introduces and discusses the fundamental distinction between the concepts of space as the container for all things and space as the positional quality of all things.
Compare Kant’s statement above to the following statement contradicting it, made by David Hume in his Treatise concerning human nature: “the ideas of space and time are […] no separate or distinct ideas, but merely those of the manner or order, in which objects exist”: “[…] ’tis impossible to conceive either a vacuum and extension without matter, or a time, when there was no succession or change in any real existence” (Hume 2007, 31). Hume is clearly advocating a position-quality concept of space (see the previous footnote).
A limiting case to a theory is understood as the theory that results from the original, more general theory when some dimensional constant of it is taken to be zero, which is just how special-relativistic spacetime results from general relativity in the limiting case of weak gravitational fields. For a detailed account of limiting relations between physical theories, see Ehlers 1986.
This latter view has, for instance, been expressed by Roger Penrose (1989, 348–373). A similar view was expressed by Richard Feynman in a letter to Victor Weisskopf dated January 4 to February 11, 1961: “[…] how can we experimentally verify that [gravitational] waves are quantized? Maybe they are not. Maybe gravity is a way that quantum mechanics fails at large distances” (Feynman papers, Box 66, Folder 7, p. 15, Caltech Archives). In current approaches to an integration of gravity with quantum theory, one can still discern the different viewpoints on the nature of spacetime of the different physics communities. Thus, most varieties of string theory (which grew out of quantum field theory) start with a special-relativistic container-model spacetime (albeit of ten or more dimensions), within which the attempt is made to unify all fundamental interactions, including gravity, in a quantum theoretical framework. A different approach (closer to the spirit of general relativity) is to ‘quantize general relativity’, thereby attempting to preserve its position-quality view of spacetime (usually referred to as background independence). Thus, in Loop Quantum Gravity, a currently successful candidate of this approach, the fundamental objects, the quanta of the gravitational field, are not in space. They are nodes in a network of relations (a spin network, technically speaking) and it is quantum superpositions of their aggregates that constitute space (Rovelli 2008, 368–369).
On the differentiation of scientific disciplines from the late eighteenth to the early twentieth centuries, for the case of the physical sciences in Germany, see Stichweh 1984 and Jungnickel and MacCormmach 1986.
The observation of this latter shift of frontier – from a divide between quantum mechanics and field theory to one between quantum field theory and general relativity – is a result of research done by Alexander Blum; see Blum, Alexander and Dean Rickles forthcoming. The very synoptic outline given in this paragraph neglects, among other things, the nuclear forces that also played an important role in the history of twentieth-century physics.
Einstein and Fokker 1914. Historically, this result was again a consequence of Einstein’s intervention; see Norton 1992. Max Abraham’s introduction of a variable line element is another case in point; see Renn 2007, 311–312.
One such counter-factual scenario assumes the implementation of the equivalence principle in Newtonian science, leading to a form of classical mechanics that involves an inertio-gravitational field curved in spacetime, so that the step to general relativity becomes almost trivial, once special relativity appears (Stachel 2007). See also Renn and Stachel (2007), who discuss the convergence of David Hilbert’s work on the foundations of physics with Einstein’s theory.
