Chapter structure
- 7.1 Van Vleck’s Two Books and the Quantum Revolution
- 7.2 Van Vleck’s Early Life and Career
- 7.3 The NRC Bulletin
- 7.4 New Research and the Move to Wisconsin
- 7.5 The Theory of Electric and Magnetic Susceptibilities
- 7.6 Kuhn Losses Revisited
- Abbreviations and Archives
- Acknowledgments
- References
- Footnotes
7.1 Van Vleck’s Two Books and the Quantum Revolution
7.1.1 Van Vleck’s Trajectory from Spectra to Susceptibilities, 1926–1932
“The chemist is apt to conceive of the physicist as some one who is so entranced in spectral lines that he closes his eyes to other phenomena.” This observation was made by the American theoretical physicist John H. Van Vleck (1899–1980) in an article on the new quantum mechanics in Chemical Reviews (Van Vleck 1928b, 493). Only a few years earlier, Van Vleck himself would have fit this characterization of a physicist to a tee. Between 1923 and 1926, as a young assistant professor in Minneapolis, he spent much of his time writing a book-length Bulletin for the National Research Council (NRC) on the old quantum theory (Van Vleck 1926b). As its title, Quantum Principles and Line Spectra, suggests, this book deals almost exclusively with spectroscopy. Only after a seemingly jarring change of focus in his research, a switch to the theory of electric and magnetic susceptibilities in gases, did he come to consider his previous focus myopic. In 1927–28, now a full professor in Minnesota, he published a three-part paper on susceptibilities in Physical Review (Van Vleck 1927a; 1927b; 1928a). This became the basis for a second book, The Theory of Electric and Magnetic Susceptibilities (Van Vleck 1932b), which he started to write shortly after he moved to Madison, Wisconsin, in the fall of 1928.
By the time he wrote his article in Chemical Reviews, Van Vleck had come to recognize that a strong argument against the old and in favor of the new quantum theory could be found in the theory of susceptibilities, a subject of marginal interest during the reign of the old quantum theory. As he wrote in the first sentence of the preface of his 1932 book:
The new quantum mechanics is perhaps most noted for its triumphs in the field of spectroscopy, but its less heralded successes in the theory of electric and magnetic susceptibilities must be regarded as one of its great achievements. (Van Vleck 1932b, vii)
What especially struck Van Vleck was that, to a large extent, the new quantum mechanics made sense of susceptibilities not by offering new results, but by reinstating classical expressions that the old quantum theory had replaced with erroneous ones. Both in his articles of the late 1920s and in his 1932 book, Van Vleck put great emphasis on this point.
His favorite example was the value of what he labeled
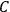 , a constant in the so-called
, a constant in the so-called 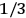 . This turns out to be a remarkably robust result in the classical theory, in the sense that it is largely independent of the model used for molecules with permanent electric dipoles. In the old quantum theory, the value of
. This turns out to be a remarkably robust result in the classical theory, in the sense that it is largely independent of the model used for molecules with permanent electric dipoles. In the old quantum theory, the value of
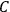 was much larger and, more disturbingly, as no experimental data were available to rule out values substantially different from the classical one, extremely sensitive to the choice of model and to the way quantum conditions were imposed. By contrast, the new quantum theory, like the classical theory, under very general conditions gave
was much larger and, more disturbingly, as no experimental data were available to rule out values substantially different from the classical one, extremely sensitive to the choice of model and to the way quantum conditions were imposed. By contrast, the new quantum theory, like the classical theory, under very general conditions gave
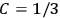 . Van Vleck saw this regained robustness as an example of what he called “spectroscopic stability” (Van Vleck 1927a, 740). New experiments also now began to provide empirical evidence for this value and Van Vleck produced new and better proofs for the generality of the result, both in classical theory and in the new quantum mechanics. From this new vantage point, Van Vleck clearly recognized that the instability of the value for
. Van Vleck saw this regained robustness as an example of what he called “spectroscopic stability” (Van Vleck 1927a, 740). New experiments also now began to provide empirical evidence for this value and Van Vleck produced new and better proofs for the generality of the result, both in classical theory and in the new quantum mechanics. From this new vantage point, Van Vleck clearly recognized that the instability of the value for
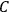 in the old quantum theory had been a largely unheeded indication of its shortcomings.
in the old quantum theory had been a largely unheeded indication of its shortcomings.
The constant
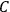 also comes into play if we want to determine the dipole moment
also comes into play if we want to determine the dipole moment
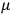 of a polar molecule such as HCl. Given a gas of these molecules, one can calculate
of a polar molecule such as HCl. Given a gas of these molecules, one can calculate
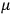 using a measurement of the dielectric constant: the greater the value of
using a measurement of the dielectric constant: the greater the value of
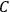 , the smaller the value of
, the smaller the value of
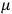 . Because of the instability of the value of
. Because of the instability of the value of
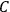 , Van Vleck (1928b) pointed out that, “[t]he electrical moment of the HCl molecule […] has had quite a history” (494).
, Van Vleck (1928b) pointed out that, “[t]he electrical moment of the HCl molecule […] has had quite a history” (494).
Fig. (7.1) shows the table with which Van Vleck illustrated this checkered history. The result for whole quanta was found by 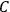 increased by a factor of almost 14 between 1912 and 1926, reducing
increased by a factor of almost 14 between 1912 and 1926, reducing
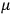 to a third of its classical value. “Fortunately [in the new quantum mechanics] the electrical moment of the HCl molecule reverts to its classical 1912 value” (Van Vleck 1928b, 494).
to a third of its classical value. “Fortunately [in the new quantum mechanics] the electrical moment of the HCl molecule reverts to its classical 1912 value” (Van Vleck 1928b, 494).

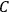 in the Langevin-Debye formula and of the electric moment
in the Langevin-Debye formula and of the electric moment
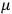 of HCl in classical theory, the old quantum theory, and quantum mechanics (Van Vleck 1928b, 494).
of HCl in classical theory, the old quantum theory, and quantum mechanics (Van Vleck 1928b, 494).Fig. 7.1: The values of the constant
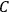 in the Langevin-Debye formula and of the electric moment
in the Langevin-Debye formula and of the electric moment
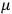 of HCl in classical theory, the old quantum theory, and quantum mechanics (Van Vleck 1928b, 494).
of HCl in classical theory, the old quantum theory, and quantum mechanics (Van Vleck 1928b, 494).
These observations, including the table, are reprised in his book on susceptibilities (Van Vleck 1932b, 107). In fact, these fluctuations in the values of
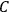 and
and
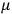 so impressed Van Vleck that the first two columns of this table can still be found in his 1977 Nobel lecture (Van Vleck 1992b, 356).
so impressed Van Vleck that the first two columns of this table can still be found in his 1977 Nobel lecture (Van Vleck 1992b, 356).
Van Vleck’s 1932 book on susceptibilities was much more successful than his Bulletin on the old quantum theory, which was released just after the quantum revolution of 1925–26. The Bulletin, as its author liked to say with characteristic self-deprecation, “in a sense was obsolete by the time it was off the press” (Van Vleck 1971, 6, our emphasis). The italicized qualification is important. In the late 1920s and early 1930s, physicists could profitably use the Bulletin despite the quantum revolution. The 1932 book, however, became a classic in the field it helped spawn. Interestingly, given that it grew out of work on susceptibilities in gases, the field in question is solid-state physics. In a biographical memoir about Van Vleck for the National Academy of Sciences (NAS), condensed-matter icon
In this paper we follow Van Vleck’s trajectory from his 1926 Bulletin on spectra to his 1932 book on susceptibilities. Both books, as we will see, loosely qualify as textbooks. As such, they provide valuable insights about the way pedagogical texts written in the midst (the 1926 Bulletin) or the aftermath (the 1932 book) of a scientific revolution reflect such dramatic upheavals.
7.1.2 Kuhn Losses, Textbooks, and Scientific Revolutions
The old quantum theory’s trouble with susceptibilities, masked by its success with spectra, is a good example of what is known in the history and philosophy of science literature as a Kuhn loss. Roughly, a 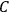 in the
in the
Incidentally, both Thomas S. Kuhn and
In 1963,
I showed that the factor one-third [in theLangevin-Debye formula for susceptibilities] got restored in quantum mechanics, whereas in the old quantum theory, it had all kinds of horrible oscillations […] you got some wonderful nonsense, whereas it made sense with the new quantum mechanics. I think that was one of the strong arguments for quantum mechanics. One always thinks of its effect and successes in connection with spectroscopy, but I remember Niels Bohr saying that one of the great arguments for quantum mechanics was its success in these non-spectroscopic things such as magnetic and electric susceptibilities.1
To the best of our knowledge, Kuhn never used the “wonderful nonsense” Van Vleck is referring to here as an example of a Kuhn loss. Still, one can ask whether the example bears out Kuhn’s general claims about
7.1.3 Kuhn Losses
The concept of a
In the transition from classical theory to the old quantum theory, gains in spectroscopy apparently outweighed losses in the theory of susceptibilities just as, at least until the early 1920s, they outweighed losses in dispersion theory. The former Kuhn loss was only regained in the new quantum theory,3 while the latter was recovered in the dispersion theory of
Strictly speaking, of course, when we talk about
Although they are both Kuhn losses of the old quantum theory, the one in susceptibility theory is of a different kind than the one in dispersion theory. In the case of dispersion, there was clear experimental evidence all along for the key feature of the classical theory that was lost in the old quantum theory and recovered in the
The key feature in the case of dispersion is that anomalous dispersion—the phenomenon that in certain frequency ranges the index of refraction gets smaller rather than larger with increasing frequency4—occurs around the absorption frequencies of the dispersive medium. This is in accordance with the classical dispersion theories of
[T]he positions of maximal dispersion and absorption do not lie at the position of the emission lines of hydrogen but at the position of the mechanical frequencies of the model […] the conclusion seems unavoidable to us that the foundations of the Debye-Davysson [sic] theory are incorrect. (Epstein 1922, 107–108; emphasis in the original; quoted and discussed by Duncan and Janssen 2007, 580–581)
By contrast, it was only after the new quantum theory had restored the classical value
 in the
in the
When 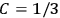 , he did not blink an eye. He just stated matter-of-factly that “the numerical factor in the final formula for the polarization depends on the specific model […] while in the classical theory the
, he did not blink an eye. He just stated matter-of-factly that “the numerical factor in the final formula for the polarization depends on the specific model […] while in the classical theory the 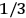 hold generally” (Pauli 1921, 325). In the conclusion of his paper, Pauli exhorted experimentalists to measure the temperature-dependence of the dielectric constant of hydrogen halides such as HCl, adding that this “should not pose any particular difficulties” (ibid., 327). Noting that his quantum theory predicted a much smaller value for the electric dipole moment
hold generally” (Pauli 1921, 325). In the conclusion of his paper, Pauli exhorted experimentalists to measure the temperature-dependence of the dielectric constant of hydrogen halides such as HCl, adding that this “should not pose any particular difficulties” (ibid., 327). Noting that his quantum theory predicted a much smaller value for the electric dipole moment
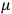 of HCl than the classical theory (
of HCl than the classical theory (
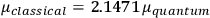 ; cf. the table in fig. 3.2), he suggested that this might provide a way to decide between the two theories. The distance between the two nuclei in, say, a HCl molecule could accurately be determined on the basis of spectroscopic data. This distance, Pauli argued, gives an upper bound on the dipole length
; cf. the table in fig. 3.2), he suggested that this might provide a way to decide between the two theories. The distance between the two nuclei in, say, a HCl molecule could accurately be determined on the basis of spectroscopic data. This distance, Pauli argued, gives an upper bound on the dipole length
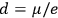 between the charges
between the charges
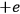 and
and
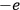 forming the dipole in this case. Hence, he concluded, “if the classical formula for the dielectric constant gives a dipole length that is greater than the nuclear separation extracted from infrared spectra, the formula must be rejected” (Pauli 1921, 327, emphasis in the original).
forming the dipole in this case. Hence, he concluded, “if the classical formula for the dielectric constant gives a dipole length that is greater than the nuclear separation extracted from infrared spectra, the formula must be rejected” (Pauli 1921, 327, emphasis in the original).
Three years later, the experimentalist 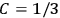 became available (Van Vleck 1932b, 61). The
became available (Van Vleck 1932b, 61). The
7.1.4 Textbooks and Kuhn Losses
Kuhn (1996, chap. 11) famously identified textbooks as the main culprit in rendering the disruption of normal science by scientific revolutions invisible. Textbooks, he argued, by their very nature must present science as a cumulative enterprise. This means that
address themselves to an already articulated body of problems, data, and theory, most often to the particular set of paradigms6 to which the scientific community is committed at the time they are written […] [B]eing pedagogic vehicles for the perpetuation of normal science […] [they] have to be rewritten in the aftermath of each scientific revolution, and, once rewritten, they inevitably disguise not only the role but the very existence of the revolutions that produced them […] [thereby] truncating the scientist’s sense of his discipline’s history. (Kuhn 1996, 136–137)
When he wrote this passage,
The two monographs by Van Vleck examined in this paper would seem to qualify as (graduate) textbooks even though under a strict and narrow definition of the genre they might not. Most of their actual readers may have been research scientists but they were written with the needs of students in mind and both books saw some classroom use. Student notes for a two-semester course on quantum mechanics that Van Vleck offered in Wisconsin in 1930–31 show that, despite the quantum revolution that had supposedly made it obsolete four years earlier, Van Vleck was still using his NRC Bulletin as the main reference for almost two-thirds of the first semester.7 It is unclear whether Van Vleck himself ever used his 1932 book on susceptibilities in his classes. However, one of his colleagues at Wisconsin,
So one can reasonably ask how well Van Vleck’s two books fit with Kuhn’s seductive picture of how the regrouping of a scientific community in response to a scientific revolution is reflected in the textbooks it produces. It will be helpful to separate two aspects of this picture: how textbooks delineate and orient further work in their (sub-)disciplines, and how, in doing so, they inevitably distort the prehistory of these (sub-)disciplines and paper over
Van Vleck’s NRC Bulletin confirms several of his former student’s generalizations about textbooks. The Bulletin is organized around the correspondence principle as a strategy for tackling problems mostly in atomic spectroscopy. Van Vleck thus took the approach he,
Those engaged in work that was marginalized in this way predictably took exception. In a review of the Bulletin, one such colleague,
Selection of, arrangement of, and space devoted to the offerings is heavily influenced by subjective viewpoints and cannot win every reader’s approval everywhere. Instead of the presumably available option of letting all fundamental connections emerge systematically, the author has preferred to put up front what is felt to be the internally most unified part of the quantum theory as it has developed so far, followed by more or less isolated applications to specific problems. (Smekal 1927, 63)
The way in which correspondence-principle techniques take center stage in Van Vleck’s book provides a nice example of how textbooks transmit what
I mean, initially, the concrete problem solutions that students encounter from the start of their scientific education, whether in laboratories, on examinations or at the ends of chapters in science texts. To these shared examples should, however, be added at least some of the technical problem-solutions found in the periodical literature that scientists encounter during their post-educational research careers and that also show them by example how their job is to be done. (Kuhn 1996, 187)
Van Vleck’s Bulletin presented such “technical problem-solutions found in the periodical literature” in a more didactic text that should help its readers become active contributors to this literature themselves.
Confirming another article of Kuhnian doctrine, the problem with susceptibilities, a 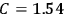 for whole quanta in the table in fig. (3.2) (Fellows 1985, 136).
for whole quanta in the table in fig. (3.2) (Fellows 1985, 136).
Whereas the Bulletin passes over the Kuhn loss in the theory of susceptibilities in silence, the Kuhn loss in dispersion theory in that same transition is flagged prominently. It is easy to understand why. By the time Van Vleck wrote his Bulletin,
In his 1932 book, as we will see in secs. (7.5.2–7.5.5), Van Vleck made even more elaborate use of the recovered Kuhn loss in susceptibility theory to promote his new quantum-mechanical treatment of susceptibilities. He devoted a whole chapter of the book to the problems of the old quantum theory in this area. Of course, the
Like the Bulletin, the 1932 book provided its readers with all the tools they needed to become researchers in the field it so masterfully mapped out for them. Had the correspondence-principle approach to atomic physics been moribund by the time the Bulletin saw print, the approach to electric and magnetic susceptibilities championed in the 1932 book would prove to be remarkably fruitful.
7.1.5 Continuity and Discontinuity in Scientific Revolutions
A couple of
The 1932 book provides the clearest example of this. As mentioned above, Van Vleck devoted an entire chapter to the old quantum theory, putting the problems it ran into with susceptibilities on full display. Yet he conveniently neglected to mention that there had been no clear empirical evidence exposing these problems.
That said, there were many elements in older theories that helped rather than hindered Van Vleck in achieving these objectives. As a result, much of the continuity that can be discerned in the discussions of classical theory and quantum theory in the NRC Bulletin is not, as Kuhn would have it, an artifact of how history is inevitably rewritten in textbooks, but actually matches the historical record tolerably well. Despite its misleading treatment of the experimental state of affairs in the early 1920s, the same can be said about the 1932 book. The final two clauses of the passage from Structure quoted above (“inevitably disguise […]” and “truncating […]”) are clearly too strong.
On the Kuhnian picture of scientific revolutions as paradigm shifts akin to Gestalt switches, it is hard to understand how a post-revolutionary textbook could make the prehistory of its subject matter look more or less continuous and thereby perfectly suitable to its pedagogical objectives without seriously disguising, distorting, and truncating that prehistory. An important part of the explanation, at least in the case of these two books by Van Vleck, is the continuity of mathematical techniques through the conceptual upheavals that mark the transition from classical theory to the old quantum theory, and finally to modern quantum mechanics.
In his recent book, Crafting the Quantum, on the Sommerfeld school in theoretical physics, Suman Seth (2010) makes a similar point. He reconciles the continuous and the discontinuous aspects of the development of quantum theory in the 1920s by emphasizing, as we do, the continuity of mathematical techniques. Scientific revolutions, he writes, “are revolutions of conceptual foundations, not of puzzle-solving techniques. Most simply: Science sees revolutions of principles, not of problems” (Seth 2010, 268). To illustrate his point, Seth quotes Arnold Sommerfeld, who wrote in 1929: “The new development does not signify a revolution, but a joyful advancement of what was already in existence, with many fundamental clarifications and sharpenings” (ibid., 266).
Given the radical conceptual changes involved in the transition from classical physics to quantum physics, it is important to keep in mind that there was at the same time great continuity of mathematical structure in this transition. Both the old quantum theory and matrix mechanics, for instance, retain, in a sense, the laws of classical physics. The old quantum theory just put some additional constraints on the motions allowed by Newtonian mechanics. The basic idea of matrix mechanics, as reflected in the term Umdeutung (reinterpretation) in the title of the paper with which
In the old quantum theory, techniques from perturbation theory in celestial mechanics were used to analyze electron orbits in atoms classically as a prelude to the translation of the results into quantum formulas under the guidance of the correspondence principle (Duncan and Janssen 2007, 592–593, 627–637). This is the procedure that led
One way to highlight the continuity of Van Vleck’s trajectory from spectra to susceptibilities is to note that the derivation of the
The remarkable continuity of mathematical structures and techniques in the transitions from classical theory to the old quantum theory, and then to modern quantum mechanics makes it perfectly understandable that Van Vleck could still use his 1926 Bulletin in his courses on quantum mechanics in the early 1930s. It also explains how Van Vleck could make such rapid progress once he hit upon the problem of susceptibilities not long after he completed the Bulletin and mastered matrix mechanics.
Kuhn had a tendency to see only discontinuity in paradigm shifts. This intense focus on discontinuity is what lies behind his fascination with
Whether one sees continuity or discontinuity in the transition from classical physics to quantum physics depends, to a large extent, on one’s perspective. The historian trying to follow the events as they unfolded on the ground, will probably mainly see continuities. The historian who takes a bird’s eye view and compares the landscapes before and after the transition will most likely be struck first and foremost by discontinuities. A final twist in our story about the recovered Kuhn loss in Van Vleck’s 1932 book nicely illustrates this difference in perspective.
Van Vleck covered the troublesome recent history of its subject matter in chap. V, “Susceptibilities in the old quantum theory contrasted with the new.” This chapter, as we will show in more detail in secs. (7.5.2–7.5.5), allows us to see important elements of continuity in the transition from the old to the new quantum theory. Toward the end of his life, Van Vleck began revising his 1932 classic with the idea of publishing a new edition (Fellows 1985, 258, 262–263, 266).9 Wanting to add a chapter on modern developments without changing the total number of chapters, he intended to cut chap. V, on the grounds that by then it only had historical value.10 Even in 1932 he began the chapter apologizing to his readers that “it may seem like unburying the dead to devote a chapter to the old quantum theory” (Van Vleck 1932b, 105). Note also the one reservation Anderson (1987, 509) expressed about the book in his NAS memoir: “It is marked—perhaps even slightly marred, as a modern text for physicists poorly trained in classical mechanics—by careful discussion of the ways in which quantum mechanics, the old quantum theory, and classical physics differ.” As it happened, the new edition of the book never saw the light of day, but if it had, it would have been a confirming instance of an amended version of Kuhn’s thesis, namely that, going through multiple editions, textbooks eventually suppress or at least sanitize the history of their subject matter and paper over
7.1.6 Van Vleck as Teacher
Although it will be clear from the preceding subsections that our main focus in this paper is not on Van Vleck’s books as pedagogical tools, it seems appropriate to devote a short subsection to Van Vleck as a teacher.
A good place to start is to compare testimony by
By the 1940s […] his teaching style had become unique, and is remembered with fondness by everyone I spoke to. Most of the material was written in his inimitable scrawl on the board […] Especially in group theory [taught from (Wigner 1931) in the original German], his intuitive feeling for the subject often bewildered us as he scribbled […] in an offhand shorthand to demonstrate what we thought were exceedingly abstruse points. (Anderson 1987, 524)
Anderson’s assessment is actually consistent with Kuhn’s, even though the latter evidently did not share his fellow student’s enthusiasm for the unique style of their advisor: “One of the courses that I then took was group theory with Van Vleck. And I found that somewhat confusing […] Van Vleck was not a terribly good teacher” (Baltas et.al. 2000, 272).
Van Vleck’s teaching style must have been less idiosyncratic in his earlier years. As
John Van Vleck was my professor at Wisconsin. The first year I was there he gave a course in quantum mechanics. No one wanted to take a degree that year. Everyone put it off because it was useless—there weren’t any jobs. The next year Van had the same bunch of students, so he gave us advanced quantum mechanics. The year after that he gave us advanced quantum mechanics II. Van was extremely good, a good teacher and an outstanding physicist.11 (Serber 1992, xxiv)
Anderson offered the following explanation for Van Vleck’s effectiveness as a teacher:
In all of his classes […] he used two basic techniques of the genuinely good teacher. First, he presented a set of carefully chosen problems […] Second, he supplied a “crib” for examination study, which we always thought was practically cheating, saying precisely what could be asked on the exam. It was only after the fact that you realized that it contained every significant idea of the course. (Anderson 1987, 524–525)
Fig. 7.2: Van Vleck between two fans at 1300 Sterling Hall, University of Wisconsin–Madison, ca. 1930 (picture courtesy of John Comstock).
Even before the Great Depression, students sometimes took Van Vleck’s quantum course more than once.
In his first year at Madison, 1928–29, Van Vleck immediately started supervising two postdocs,
Physics 212, “Quantum mechanics and atomic structure,” was the only lecture course Van Vleck offered during his first few years in Wisconsin (ibid., 230). It was not until 1931–33, the period described by
7.1.7 Structure of Our Paper
The balance of this paper is organized as follows. In sec. (7.2), we sketch Van Vleck’s early life against the backdrop of theoretical physics coming of age and maturing in the United States. Our main focus is on his years in Minneapolis leading up to the writing of his NRC Bulletin (1923–26). Throughout the paper, but especially in the more biographical secs. (7.2) and (7.4), we make heavy use of the superb dissertation on Van Vleck by Fred Fellows (1985). In sec. (7.3), we turn to the Bulletin itself (Van Vleck 1926b). In sec. (7.3.1), we recount how what had originally been conceived as a review article of average length eventually ballooned into a 300-page book. In sec. (7.3.2) we give an almost entirely qualitative discussion of its contents, focusing on the derivation of
7.2 Van Vleck’s Early Life and Career
John Hasbrouck Van Vleck (1899–1980) was born in Middletown, Connecticut, to Edward Burr Van Vleck and Hester Laurence Van Vleck (née Raymond). In 1906 the family moved to Madison, Wisconsin, where his father was appointed professor of mathematics.13 He had been named after his grandfather, John Monroe Van Vleck, but his mother, not fond of her father-in-law, called him Hasbrouck (Fellows 1985, 6–8). To his colleagues, he would always be Van. A nephew of Van’s wife, Abigail June Pearson (1900–1989), recalls that a telegram from Japan congratulating Van Vleck on winning the Nobel prize was addressed to “Professor Van” (John Comstock, private communication).
In 1916 Van Vleck began his undergraduate studies at the University of Wisconsin, where he eventually majored in physics. In the fall of 1920, he enrolled at Harvard as a graduate student in physics.14 He took
The following year, Van Vleck accepted a position as an instructor in Harvard’s physics department. This demanding job left him with little time for his own work. Most of his time was spent preparing for lectures and lab sessions (Fellows 1985, 49). In the midst of this daily grind, the job offer that arrived from the University of Minnesota in early 1923 must have looked especially attractive. As Van Vleck (1992a, 351) would reflect later, it was an “unusual move” for such an institution at that time—indicative, one may add, of the American physics community’s growing recognition of the importance of quantum theory—to offer him an assistant professorship “with purely graduate courses to teach.”
At first, Van Vleck was hesitant to accept the position.17 He and
In October 1924, after a preliminary report in the Journal of the Optical Society of America (Van Vleck 1924a), a two-part paper appeared in Physical Review in which Van Vleck (1924b; 1924c) used correspondence-principle techniques to analyze the interaction between matter and radiation in the old quantum theory. Its centerpiece was Van Vleck’s own correspondence principle for absorption, but the paper also contains a detailed derivation of the
After his 1924 paper, however, Van Vleck did not push this line of research any further. He had meanwhile been ‘invited’ to produce the volume to which we now turn our attention. Its completion would occupy nearly all of his available research time for the next two years.
7.3 The NRC Bulletin
7.3.1 Writing the Bulletin
Later in life, when interviewed by
I was already writing some chapters on that on rainy days in Switzerland in 1924. I would say I started writing that perhaps beginning in the spring of 1924, and finished it in late 1925. I worked on it very hard that summer […] I was sort of a “rara avis” at that time. I was a young theoretical physicist presumably with a little more energy than commitments than the older people interested in these subjects, so they asked me if I’d write this thing. I think it was by invitation rather than by my suggestion.18
The invitation had come from
The committees organized the Bulletins of the NRC, which existed to present “contributions from the National Research Council […] for which hitherto no appropriate agencies of publication [had] existed” (Swann et.al. 1922, 173–174). This sounds rather vague and overly inclusive, and on reading the motley assortment of topics covered by the Bulletins through 1922, one finds that it was rather vague and overly inclusive. The Bulletins served to disseminate whatever information the myriad committees deemed important. A brief list of topics covered by these publications includes “The national importance of scientific and industrial research,” “North American forest research,” “The quantum theory,” “Intellectual and educational status of the medical profession as represented in the United States Army,” and “The scale of the universe” (ibid.). The Bulletins tended to be short, averaging about 75 pages. Several were even shorter, coming in under 50 pages. The longest at the time Van Vleck was invited to write one on line spectra was a 172-page book, Electrodynamics of Moving Media (Swann et.al. 1922). It had been written by four authors, including
Given the Bulletin’s publication history, Van Vleck was not making an unreasonable commitment when he accepted
As we saw, Van Vleck later recalled having begun his Bulletin in the spring of 1924, but he must have started much earlier than that. In March 1924, Foote returned a draft to Van Vleck along with extensive comments. “This has been read very carefully by
Perhaps
Like you I “am wondering” when my paper for the Research Council will ever be ready. I am sorry to be progressing so slowly but I hope you realize that I am devoting to this report practically all of my time not occupied with teaching duties. I still hope to have the manuscript ready by Christmas except for finishing touches.22
Van Vleck would blow the Christmas deadline as well. It was not until August that he submitted a new draft:
I hope the bulletin will be satisfactory, as with the exception of one three-month period it has taken all my available research time for two years.
You wrote me that the bulletin should be “fairly complete.” My only fear is that it may be too much so. I made sure to include references to practically all the important theoretical papers touching on the subjects covered in the various chapters. Four new chapters have been included since an early draft of the manuscript was sent to you a year ago […]
You will note that I have used a new title “Quantum Principles and Line-Spectra” as this is much briefer and perhaps more a-propos than “The Fundamental Concepts of the Quantum Theory of Line-Spectra.”23
It is worth noting the change in title. The old quantum theory was strongly focused on the phenomena of line spectra. Van Vleck’s new title conveys at once this focus even as he had significantly broadened the scope of his project.
Even when
It is clear that however the project began, and whatever Van Vleck’s initial expectations, in the end the Bulletin was intended by its author as a comprehensive and up-to-date review of quantum theory. This makes it useful not only as a review of the old quantum theory, but also as a window into Van Vleck’s own perception and understanding of the field.
Despite some critical notes,25 the Bulletin was “on the whole, well-received” (Fellows 1985, 88). Van Vleck must have read
This excellent bulletin will prove extremely useful to all who are interested in atomic physics […] [T]he fundamental theorems of Hamiltonian dynamics and perturbation methods of quantization are treated in a very readable fashion […] The chapter on the quantization of neutral helium is authoritative […] The author’s treatment of the “correspondence principle” is refreshingly clear […] The whole book is surprisingly up-to-date. Even the theory of spinning electrons and matrix dynamics are touched upon. It is to be hoped that this report will run through many revised editions as quantum theory progresses, for it fills a real need. (Ruark 1926)
In fact,
Many readers will not agree with the author’s conclusion that“Kramers’s dispersion theory […] furnishes by far the most satisfactory theory of dispersion” [Van Vleck 1926b, 156–157] […] the reviewer believes that a final solution cannot be achieved until we have a much more thorough knowledge of the dispersion curves of monatomic gases and vapors. (Ruark 1926)
Subsequent developments would prove that Van Vleck’s confidence in the Kramers dispersion formula was well-placed. It carried over completely intact to the new quantum mechanics (Duncan and Janssen 2007, 655).
7.3.2 The Bulletin and the Correspondence Principle
The central element in Van Vleck’s presentation of the old quantum theory in his NRC Bulletin is the correspondence principle. It forms the basis of 11 out of a total of 13 chapters.27 As it says in the preface,
Bohr’s correspondence principle is used as a focal point for much of the discussion in Chapters I–X. In order to avoid introducing too much mathematical analysis into the discussion of the physical principles underlying the quantum theory, the proofs of certain theorems are deferred to Chapter XI, in which the dynamical technique useful in the quantum theory is summarized. (Van Vleck 1926b, 3)
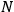 , the orbital frequencies of the
, the orbital frequencies of the
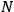 -th and the
-th and the
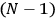 -th orbit and the frequency of the radiation emitted or absorbed when an electron jumps from one to the other approach each other. This is the core of what later came to be called the correspondence principle.
-th orbit and the frequency of the radiation emitted or absorbed when an electron jumps from one to the other approach each other. This is the core of what later came to be called the correspondence principle.
By the early 1920s, the correspondence principle had become a sophisticated scheme used by several researchers for connecting formulas in classical mechanics to formulas in the old quantum theory. The most important result of this approach was the
As a concrete example of the use of the correspondence principle in the old quantum theory in the early 1920s, we sketch Van Vleck’s derivation of the Kramers dispersion formula.28 This formula and what Van Vleck (1926b, 162) called the “correspondence principle for dispersion” are presented in a section of only two and a half pages in chap. X of the NRC Bulletin (ibid., sec. 51, 162–164). The reason that Van Vleck could be so brief at this point is that the various ingredients needed for the derivation of the formula are all introduced elsewhere in the book, especially in chap. XI on mathematical techniques. At 50 pages, this is by far the longest chapter of the Bulletin.
Consider some (multiply-)periodic system—anything from a charged simple harmonic oscillator to an electron orbiting a nucleus—struck by an electromagnetic wave of a frequency
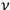 not too close to that system’s characteristic frequency
not too close to that system’s characteristic frequency
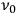 or frequencies
or frequencies
 . The
. The
To obtain the
As with all such derivations in the old quantum theory, the part involving classical mechanics called for advanced techniques borrowed from celestial mechanics. As we mentioned in sec. (7.2), Van Vleck had thoroughly mastered these techniques as a graduate student at Harvard. Decades later, when the Dutch Academy of Sciences awarded him its prestigious Lorentz medal, Van Vleck related an anecdote in his acceptance speech that demonstrates his early mastery of this material:
In 1924 I was an assistant professor at the University of Minnesota. On an American trip,[Paul] Ehrenfest gave a lecture there […] [He] said he would like to hear a colloquium by a member of the staff. I was selected to give a talk on my “Correspondence Principle for Absorption” [Van Vleck 1924a, 1924b, 1924c] […] I remember Ehrenfest being surprised at my being so young a man. The lengthy formulas for perturbed orbits in my publication on the three-body problem of the helium atom [Van Vleck 1922] had given him the image of a venerable astronomer making calculations in celestial mechanics. (Van Vleck 1974, 9; quoted by Duncan and Janssen 2007, 627)
Van Vleck put his expertise in classical mechanics to good use. Using canonical perturbation theory in action-angle variables, he derived an expression in classical mechanics for the dipole moment of a charged multiply-periodic system hit by an electromagnetic wave of small amplitude, which could then be translated into a quantum-theoretical expression.
In general coordinates and their conjugate momenta
 (where
(where
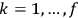 , with
, with
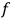 the number of degrees of freedom), Hamilton’s equations are:
the number of degrees of freedom), Hamilton’s equations are:
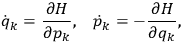
|
7.1 |
where
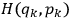 is the Hamiltonian and dots indicate time derivatives. Given the Hamiltonian of some multiply-periodic system, one can often find special coordinates,
is the Hamiltonian and dots indicate time derivatives. Given the Hamiltonian of some multiply-periodic system, one can often find special coordinates,
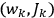 , called action-angle variables, such that the Hamiltonian in the new coordinates only depends on the new momenta, the action variables
, called action-angle variables, such that the Hamiltonian in the new coordinates only depends on the new momenta, the action variables
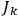 , and not on the new coordinates, the angle variables
, and not on the new coordinates, the angle variables
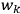 . In that case,
. In that case,
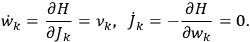
|
7.2 |
The first of these equations shows what makes the use of action-angle variables so attractive in celestial mechanics. It makes it possible to extract the characteristic periods of the system from the Hamiltonian without having to know the details of the orbit.
Action-angle variables played a central role in the old quantum theory. They are used to formulate the 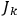 and the original position and momentum variables
and the original position and momentum variables
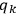 and
and
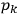 is:
is:
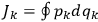 , where the integral is over one period of the motion. The Sommerfeld-Wilson quantum conditions restrict the classically allowed orbits to those satisfying
, where the integral is over one period of the motion. The Sommerfeld-Wilson quantum conditions restrict the classically allowed orbits to those satisfying
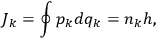
|
7.3 |
where
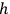 is
is 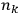 ’s are integers.
’s are integers.
For orbits with high values for all quantum numbers, there is only a small difference between the values of the Hamiltonian for
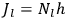 and for
and for
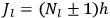 (with the values of all
(with the values of all
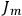 ’s with
’s with
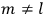 fixed). The differential quotients
fixed). The differential quotients
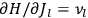 in the first equation in eq. (7.2) can then be approximated by difference quotients:
in the first equation in eq. (7.2) can then be approximated by difference quotients:
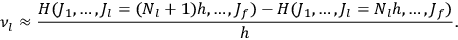
|
7.4 |
The two values of the Hamiltonian in the numerator give the energies
 and
and
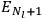 of two orbits, close to each other, with high values for all quantum numbers (all, except for the
of two orbits, close to each other, with high values for all quantum numbers (all, except for the
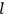 -th one, equal for the two orbits). Eq. (7.4) is thus of the form:
-th one, equal for the two orbits). Eq. (7.4) is thus of the form:
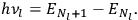
|
7.5 |
In the limit of high quantum numbers, this equation for the orbital frequency
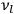 of the electron—and thereby, according to classical electrodynamics, the frequency of the radiation emitted because of the electron’s acceleration in that orbit—coincides with
of the electron—and thereby, according to classical electrodynamics, the frequency of the radiation emitted because of the electron’s acceleration in that orbit—coincides with
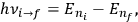
|
7.6 |
for the frequency
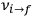 of the radiation emitted when an electron jumps from an initial orbit (quantum number
of the radiation emitted when an electron jumps from an initial orbit (quantum number
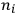 ) to a final orbit (quantum number
) to a final orbit (quantum number
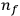 ). This asymptotic connection between this classical formula for the orbital frequencies
). This asymptotic connection between this classical formula for the orbital frequencies
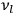 and Bohr’s quantum formula for the radiation frequencies
and Bohr’s quantum formula for the radiation frequencies
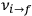 is what Van Vleck (1926b, sec. 11, 23–24) called “the correspondence theorem for frequencies.”
is what Van Vleck (1926b, sec. 11, 23–24) called “the correspondence theorem for frequencies.”
Such asymptotic connections can be used in two ways, either to check that a given quantum formula reduces to its classical counterpart in the limit of high quantum numbers, or to make an educated guess on the basis of the classical formula assumed to be valid for high quantum numbers as to what its quantum-theoretical counterpart, valid for all quantum numbers, might be. While
To derive a formula for the classical dipole moment from which its counterpart in the old quantum theory can be constructed (or against which it can be checked), one treats the electric field of the electromagnetic wave striking the periodic system under consideration as a small perturbation of the system in the absence of such disturbances. The full Hamiltonian
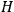 is then written as the sum of an unperturbed part
is then written as the sum of an unperturbed part
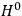 and a small perturbation
and a small perturbation
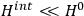 (where ‘int’ stands for ‘interaction’). Using action-angle variables in such perturbative calculations, one can derive the formula for the classical dipole moment without having to know anything about the dynamics of the unperturbed system other than that it is solvable in these variables.30
(where ‘int’ stands for ‘interaction’). Using action-angle variables in such perturbative calculations, one can derive the formula for the classical dipole moment without having to know anything about the dynamics of the unperturbed system other than that it is solvable in these variables.30
Once again,  for the full Hamiltonian
for the full Hamiltonian
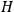 , Van Vleck continued to use action-angle variables
, Van Vleck continued to use action-angle variables
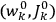 for the unperturbed Hamiltonian
for the unperturbed Hamiltonian
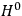 even when dealing with the full Hamiltonian
even when dealing with the full Hamiltonian
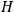 . As Van Vleck (1926b, 200) explicitly noted,
. As Van Vleck (1926b, 200) explicitly noted,
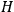 will in general depend on both the
will in general depend on both the
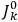 ’s and the
’s and the
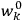 ’s, so
’s, so
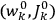 are not action-angle variables for
are not action-angle variables for
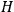 , but one can still use them to describe the behavior of the full system with interaction.31 As we will see in sec. (7.5.3), Van Vleck (1932b, 38) likewise used action-angle variables for the unperturbed Hamiltonian in his later calculations of susceptibilities.32
, but one can still use them to describe the behavior of the full system with interaction.31 As we will see in sec. (7.5.3), Van Vleck (1932b, 38) likewise used action-angle variables for the unperturbed Hamiltonian in his later calculations of susceptibilities.32
The classical formula Van Vleck eventually arrived at for the dipole moment of a multiply-periodic system has the form of a derivative with respect to the action variables
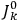 of an expression involving squares of the amplitudes of the Fourier components and the characteristic frequencies
of an expression involving squares of the amplitudes of the Fourier components and the characteristic frequencies
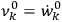 of the motion of the unperturbed system. The correspondence principle, as it was understood by
of the motion of the unperturbed system. The correspondence principle, as it was understood by
1Replace the characteristic frequencies
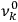 , the orbital frequencies of the motion in the unperturbed multiply-periodic systems under consideration, by the frequencies
, the orbital frequencies of the motion in the unperturbed multiply-periodic systems under consideration, by the frequencies
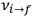 of the radiation emitted in the transition from the
of the radiation emitted in the transition from the
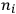 -th to the
-th to the
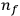 -th orbit.
-th orbit.
2Replace squares of the amplitudes of the Fourier components of this motion by transition probabilities given by the
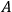 coefficients for spontaneous emission in the quantum theory of radiation proposed by
coefficients for spontaneous emission in the quantum theory of radiation proposed by
3Replace the derivatives with respect to the action variables
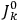 by difference quotients as in eq. (7.4). This last substitution is often attributed to Born but it was almost certainly discovered independently by Born, Kramers, and Van Vleck (Duncan and Janssen 2007, 637–638, 668).
by difference quotients as in eq. (7.4). This last substitution is often attributed to Born but it was almost certainly discovered independently by Born, Kramers, and Van Vleck (Duncan and Janssen 2007, 637–638, 668).
Although this construction guarantees that the quantum formula merges with the classical formula for high quantum numbers, it still took a leap of faith to assert that the quantum formula would continue to hold all the way down to small quantum numbers. In the case of the Kramers dispersion formula, however, there were other considerations, besides this correspondence-principle argument for it, that inspired confidence in the result.
As mentioned in sec. (7.1.3), the Kramers dispersion formula amounted to the recovery of a 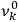 of the
of the  , at least for small quantum numbers. This is the
, at least for small quantum numbers. This is the 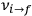 rather than the orbital frequencies
rather than the orbital frequencies
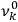 .
.
The recovery of this 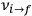 equal to that absorption frequency. The low values of these parameters then simply reflect that, for many frequencies
equal to that absorption frequency. The low values of these parameters then simply reflect that, for many frequencies
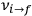 , there will only be a small number of atoms in the initial excited state (Duncan and Janssen 2007, 582–583).
, there will only be a small number of atoms in the initial excited state (Duncan and Janssen 2007, 582–583).
The correspondence-principle translation scheme outlined above was central to the research in the early 1920s of both Van Vleck (1924b; 1924c) and Born (1924). In fact, their approaches were so similar that the two men had a testy correspondence about the proper assignment of credit for various results and insights (Duncan and Janssen 2007, 569–571, 638–639). Moreover, both Born (1925) and Van Vleck (1926b) wrote a book on the old quantum theory in which they organized the material covered around the correspondence principle as they had come to understand and use it in their research.33
Both
Since the 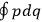 of two neighboring orbits and translating this using his Umdeutung scheme, he arrived at a corollary of the
of two neighboring orbits and translating this using his Umdeutung scheme, he arrived at a corollary of the 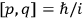 , for position and momentum in matrix mechanics (Duncan and Janssen 2007, 659–660). The Thomas-Kuhn sum rule, as Van Vleck (1926b) noted ruefully in his NRC Bulletin, “appears to have first been incidentally suggested by the writer” (152). It can be found in a footnote in the classical part of his two-part paper on his correspondence principle for absorption (Van Vleck 1924c, 359–360; cf. Duncan and Janssen 2007, 595–596, 668). By 1924, Van Vleck thus had the two key physical ingredients of
, for position and momentum in matrix mechanics (Duncan and Janssen 2007, 659–660). The Thomas-Kuhn sum rule, as Van Vleck (1926b) noted ruefully in his NRC Bulletin, “appears to have first been incidentally suggested by the writer” (152). It can be found in a footnote in the classical part of his two-part paper on his correspondence principle for absorption (Van Vleck 1924c, 359–360; cf. Duncan and Janssen 2007, 595–596, 668). By 1924, Van Vleck thus had the two key physical ingredients of
Van Vleck apparently told his former student
[T]he work is deliberately conceived as an attempt […] to ascertain the limit within which the present principles of atomic and quantum theory are valid and […] to explore the ways by which we may hope to proceed […] [T]o make this program clear in the title, I have called the present book “Vol. I;” the second volume is to contain a closer approximation to the “final” atomic mechanics […] The second volume may, in consequence, remain for many years unwritten. In the meantime let its virtual existence serve to make clear the aim and spirit of this book. (Born 1925, v)
By the time the English translation of
[I]t seems to me that the time is [sic] not yet arrived when the new mechanics can be built up on its own foundations, without any connection with classical theory […] Further, I can state with a certain satisfaction that there is practically nothing in the book which I wish to withdraw. The difficulties are always openly acknowledged […] Lastly, I believe that this book itself has contributed in some small measure to the promotion of the new theories, particularly those parts which have been worked out here in Göttingen.36 (Born 1927, xi)
Quantum mechanics continued to develop rapidly in the late 1920s (Duncan and Janssen 2013). Only three years after the English translation of his 1924 book, the sequel Born had promised in the preface to the original German edition appeared. The book, co-authored with his former student
[t]his book is the continuation of the “Lectures on atomic mechanics” published in 1925; it is the “second volume” that was announced in the preface, of which “the virtual existence should serve to make clear the aim and spirit of this book.” The hope that the veil that was still hanging over the real structure of the laws of the atom would soon be parted has been realized in a surprisingly fast and thorough fashion. (Born and Jordan 1930, v)
The authors then warned their readers that they had made a conscious effort to see how much could be done with “elementary, i.e., predominantly algebraic means” (ibid., vi). In other words, elementary quantum mechanics, for Born and Jordan, was essentially matrix mechanics. They relegated wave-theoretical methods to a future book they promised to write “as soon as time and energy permit” (ibid).
In his review of Elementary Quantum Mechanics in Die Naturwissenschaften,  -th volume is always made clear through the virtual existence of the
-th volume is always made clear through the virtual existence of the
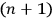 -th volume” (ibid.). Pauli’s review famously ends with the observation that “the production of the book in terms of print and paper is excellent” (ibid.).
-th volume” (ibid.). Pauli’s review famously ends with the observation that “the production of the book in terms of print and paper is excellent” (ibid.).
Contrary to Born, Van Vleck only seems to have realized how serious the problems facing the old quantum theory were after its demise. Talking to
In one of the sections of chap. VIII, sec. 35, entitled “Standard Quantum Conditions and Correspondence Theorem for Frequencies Remain Valid Even if Classical Mechanics Break [sic] Down,” he wrote:
[T]o escape from the difficulties thus encountered [in the preceding section] it appeared necessary to assume that the classical mechanics do [sic] not govern the motions of the electrons in the stationary states of atoms with more than one electron. It might seem that this bold proposal would invalidate the considerable degree of success already sometimes attained in complicated atoms […] Such successful applications, however, need not be forfeited if only we assume that the Bohr frequency condition and the standard quantum conditions retain their validity, even though the motions quantized by the latter are not in accord with ordinary dynamics in atoms with more than one electron. (Van Vleck 1926b, 108, our emphasis)
As bold as Van Vleck may have thought his proposal was, by the time his Bulletin was in print,
By the time he wrote the article about the new quantum theory in the Chemical Reviews from which we quoted at the beginning of this paper, Van Vleck had certainly understood that the transition from the old to the new quantum theory required much more radical steps than the ones he had contemplated in his NRC Bulletin. As he explained to his colleagues in chemistry,
one cannot use a meter stick to measure the diameter of an atom, or an alarm clock to record when an electron is at the perihelion of its orbit. Consequently we must not be surprised […] that models cannot be constructed with the same kind of mechanics as Henry Ford uses in designing an automobile. (Van Vleck 1928b, 468, quoted and discussed by Duncan and Janssen 2007, 666)
In the years following the Bulletin’s publication, Van Vleck’s perceptions of the old quantum theory would change a great deal. Specifically, he would come to see its shortcomings through the lens of his subsequent work on susceptibilities and his own accomplishments in this area as providing powerful arguments against the old and in favor of the new quantum theory.
7.4 New Research and the Move to Wisconsin
Only after the Bulletin was sent to press was Van Vleck able to confront matrix mechanics. By late March of 1926, he had no doubt caught up with current developments, in part through his own reading and in part through direct contact with Born, who lectured in Madison that month (Fellows 1985, 102). In January of 1926,
In April 1926, Van Vleck read a paper submitted to the Physical Review by 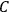 in the
in the
About a month after Van Vleck read Pauling’s paper, a paper by
I remember in particular [Tate] showing me an article by Dennison written in Copenhagen [while on an International Education Board (IEB) fellowship] which had the matrix elements for the symmetrical top. I realized this was just what was needed to compute the dielectric constant of a simple diatomic molecule. I requested Dennison’s permission to use them in advance of their appearing in print, and remember his wiring me permission to do so. I found that they made the factorin the
Debye formula […] for the susceptibility reacquire the classical value , replacing the nonsensical values yielded by the old quantum theory.42 (Van Vleck 1971, 8)
Van Vleck’s calculation was analogous to
I must confess that that rather burned me up because I felt it was quite a significant achievement in quantum theory. When I mentioned it toBohr he said “you should have got me to endorse it, it would have gone through quicker” [see also Van Vleck (1968, 1235)]. As it was, I think [Lucy] Mensing and Pauli beat me to it on being the first to publish that factor one-third. It was essentially a triple tie, though [Ralph de Laer] Kronig had it too, all three of us.43,44
Van Vleck (1971) later called it a “quadruple tie” (7), adding a paper by 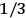 for the factor
for the factor
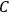 . These 1926 papers only dealt with the special case in which the rigid rotator was used to model the gas molecules.47
. These 1926 papers only dealt with the special case in which the rigid rotator was used to model the gas molecules.47
While crossing the Atlantic in June 1926, Van Vleck finished another calculation in quantum mechanics only to discover upon reaching Copenhagen that he had been scooped by
When Van Vleck returned to the United States, he found that quantum theorists were in high demand and that the publication of his NRC Bulletin had earned him a reputation as one of the few in the United States who had a grasp of the theory. He had also found time that summer to write a short report on the new quantum mechanics for the Progress Committee of the Optical Society of America (Van Vleck 1928c). Leonard R. Ingersoll at the University of Wisconsin called it “the only readable synopsis of the present situation in this difficult subject” (Fellows 1985, 162).
As Van Vleck’s fame increased, he found himself wooed more and more doggedly by other universities. From the fall of 1926 through the spring of 1928, he declined offers from the University of Chicago, Princeton, and the Mellon Institute. Many of these he rejected out of a sense of loyalty to the University of Minnesota, which had been so generous to him. The department continued to recognize Van Vleck’s value, following up with raises and promotions. In June 1926 he had become an associate professor, and only a year later he became a full professor. By the summer of 1927, having married Abigail June Pearson, a native Minnesotan, he had established family ties to the state as well. It took an offer from his alma mater to win him over, and even then he vacillated for over a year before accepting a position at the University of Wisconsin (Fellows 1985, 169–175). He arrived at Madison in time for the fall semester of 1928.
Over the same period, Van Vleck had been busy pursuing the line of inquiry that would secure him fame as an expert in magnetism. He published a three-part paper that advanced a general theory of susceptibilities (Van Vleck 1927a; 1927b; 1928a). This trilogy would form the basis for The Theory of Electric and Magnetic Susceptibilities (Van Vleck 1932b).

Fig. 7.3: Van Vleck receiving the National Medal of Science in 1966 from President Lyndon B. Johnson with Lady Bird Johnson looking on (picture courtesy of John Comstock).
Before turning to that volume in the next section, we wrap up this section with some brief comments about Van Vleck’s career after he left the Midwest. In early 1934, Van Vleck was offered an associate professorship at Harvard to replace
During World War II, Van Vleck was the head of the theory group at Harvard’s Radio Research Laboratory, thinking about ways to jam enemy radar, and a consultant to MIT’s much bigger Radiation Laboratory (Anderson 1987, 514).
From 1945 to 1949 he was chair of Harvard’s physics department (ibid., 519). In 1951, he succeeded
Even though Van Vleck spent the better part of his career at Harvard, he always retained a soft spot for Minnesota and Wisconsin. Together with
7.5 The Theory of Electric and Magnetic Susceptibilities
7.5.1 Writing the 1932 Book
In 1928 Van Vleck had been thinking about writing his own book on quantum mechanics, but he became interested that fall when
The delays were of a different nature than the trials and tribulations that had prevented a slightly younger Van Vleck from publishing his completed “article” in the NRC Bulletin. This time, he made his own original research a higher priority. He also accepted several invitations to give talks in Iowa, Minneapolis, and New York. This, and supervising the research of his graduate students and postdocs, took up most of his time during the 1928–29 school-year. He did manage to squeeze in one chapter, however. “I have actually, mirab[i]le dictu, completed one chapter of my book,” he wrote to
After spending the summer on research, he devoted all of his free time in the fall to the book and completed another chapter. The following spring, 1930, he negotiated a sabbatical leave in which he received half of his salary from Wisconsin, and made up the rest with a Guggenheim fellowship. He and Abigail went to Europe, making stops in England, Holland, and Germany. Finally, Van Vleck went to Switzerland while Abigail joined his parents for a tour of Italy. Unfortunately, when Van Vleck arrived at the Eidgenössische Technische Hochschule (ETH) in Zurich, he discovered that Pauli and other faculty were away on lengthy spring vacations (ibid, 240–241). Van Vleck turned this to his advantage:
The janitor at the ETH, fortunately, was very friendly and arranged for me to have the use of the library. I lived comfortably at the Hotel Waldhaus Dolder, and with a portable typewriter and no distractions by colloquia, social life or sight-seeing, I probably wrote more pages of my ‘Theory of Electric and Magnetic Susceptibilities’ in my first month at Zurich than in any other comparable time interval. (Van Vleck 1968, 1236, quoted by Fellows 1985, 242)
When
In June 1930, Van Vleck received an invitation to the
After receiving permission from Wisconsin, he extended his trip into the fall, finally returning in October with the book almost complete.
Reviewers immediately recognized its importance.50 Even  in the
in the
7.5.2 The 1932 Book and Spectroscopic Stability
Van Vleck’s The Theory of Electric and Magnetic Susceptibilities is remarkable both for the wide range of concepts it covers and techniques it assembles, and for the amount of discussion devoted to the historical development of the theories under consideration. Even though the main focus of the book is on gases, it ended up, as we mentioned in the introduction, setting “a standard and a style for American solid-state physics” (Anderson 1987, 524). As Van Vleck explained in the preface:
At the outset I intended to include only gaseous media, but the number of paramagnetic gases is so very limited that any treatment of magnetism not applicable to solids would be rather unfruitful. (Van Vleck 1932b, vii)
In the book, Van Vleck clearly demonstrated how his general
The book can be roughly divided into two parts, separated by an interstitial aside concerning the defects and demise of the old quantum theory. Chaps. I–IV constitute the first part. Here Van Vleck surveyed the classical theories of electric and magnetic susceptibilities. In addition to marshaling resources that will be drawn from in later chapters, Van Vleck carefully examined the failings of the classical theories, motivating the quantum-mechanical approach that is developed in the book’s second half.
Chap. V is the interstitial aside, which we will discuss in more detail in sec. (7.5.4). Chap. VI begins the book’s second half, which develops a quantum-theoretical approach to electric and magnetic susceptibilities. Like chap. XI of the NRC Bulletin on mathematical techniques, this chapter on “Quantum-Mechanical Foundations,” is by far the longest of the book. It takes up 59 pages (chap. XI of the Bulletin ran to 50 pages). It is so complete that, as we mentioned in sec. (7.1.4), it was sometimes used by itself as an introductory text in courses on the new theory. Although Van Vleck’s work had largely been in the tradition of matrix mechanics, his general exposition of quantum mechanics, in his book as well as in his lectures (as evidenced by the lecture notes mentioned in note 7), has none of the “Göttingen parochialism” (Duncan and Janssen 2008, 641) of
I have tried to correlate and intermingle the use of wave functions and of matrices, rather than relying exclusively on the one or the other, as is too often done. It is hoped that this chapter may be helpful as a presentation of the perturbation machinery of quantum mechanics, quite irrespective of the magnetic applications.51 (Van Vleck 1932b, viii)
Chaps. VII–XII interrogate and extend Van Vleck’s general
The book does exactly what a good textbook ought to do according to
The book reflects Van Vleck’s own trajectory, from his early work in the old quantum theory to the line of work in the new quantum theory that won him his reputation as one of the pioneering theorists of solid-state physics in the United States (cf. the remark by
 of some gas is
of some gas is

|
7.7 |
where
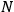 is the number of molecules,
is the number of molecules,
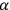 is a constant,
is a constant,
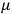 is the permanent electric moment of the molecule under consideration,
is the permanent electric moment of the molecule under consideration,
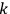 is
is 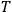 is the temperature (Van Vleck 1927a, 727; 1932b, 28).53 The first term comes from the induced moment of the molecule, resulting from the deformation of the molecule by the external electric field. The second term comes from the alignment of the permanent moment of the molecule with the field. Thermal motion will frustrate this alignment, which is expressed in the inverse proportionality to the temperature
is the temperature (Van Vleck 1927a, 727; 1932b, 28).53 The first term comes from the induced moment of the molecule, resulting from the deformation of the molecule by the external electric field. The second term comes from the alignment of the permanent moment of the molecule with the field. Thermal motion will frustrate this alignment, which is expressed in the inverse proportionality to the temperature
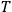 . As Van Vleck noted when he introduced the formula in his book:
. As Van Vleck noted when he introduced the formula in his book:
The idea of induced polarization is an old one […] The suggestion that part of the electric susceptibility might be due to alinement [sic] of permanent moments, resisted by temperature agitation, does not appear to have been made until 1912 byDebye [1912]. A magnetic susceptibility due entirely to the orientation of permanent moments was suggested some time previously, in 1905, by [Paul] Langevin [1905a, 1905b], and the second term of [eq. 7.7] is thus an adaptation to the electric case of Langevin’s magnetic formula. (In the electric case, a formula such as [7.7] is commonly called just the Debye formula, but we use the compound title Langevin-Debye in order to emphasize that the mathematical methods which we use to derive the second term of [eq. 7.7] apply equally well to magnetic or electric dipoles). (Van Vleck 1932b, 30)
It is this temperature-dependent second term that Van Vleck was most interested in. We can write this term as
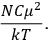
|
7.8 |
Both classical theory and quantum mechanics correctly predict that, under very general conditions,
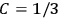 . The two theories agree except at very low temperatures, where the classical theory breaks down and where quantum mechanics gives deviations from
. The two theories agree except at very low temperatures, where the classical theory breaks down and where quantum mechanics gives deviations from
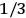 (Van Vleck 1932b, 185, 197). Other than that, the factor
(Van Vleck 1932b, 185, 197). Other than that, the factor
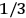 is a remarkably robust prediction of both theories. It is true for a wide range of models (e.g., dumbbell, symmetrical top) and it is independent of the choice of a
is a remarkably robust prediction of both theories. It is true for a wide range of models (e.g., dumbbell, symmetrical top) and it is independent of the choice of a
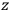 -axis for the quantization of the
-axis for the quantization of the
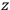 -component of the angular momentum in these models. The latter feature is an example of what Van Vleck called “spectroscopic stability.” As he put it in Part I of the trilogy that provided the backbone for his 1932 book:
-component of the angular momentum in these models. The latter feature is an example of what Van Vleck called “spectroscopic stability.” As he put it in Part I of the trilogy that provided the backbone for his 1932 book:
[T]he high spectroscopic stability characteristic of the new quantum mechanics is the cardinal principle underlying the continued validity of theLangevin-Debye formula. We shall not attempt a precise definition of the term “spectroscopic stability.”54 It means roughly that the effect of orientation or of degeneracy in general is no greater than in the classical theory, and this usually implies that summing over a discrete succession of quantum-allowed orientations gives the same result as a classical average over a continuous distribution.55 (Van Vleck 1927a, 740)
The old quantum theory gave values for
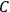 much greater than
much greater than
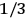 , as
, as 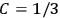 for this special case, as did
for this special case, as did
That the susceptibility of a gas of rigid rotators does not depend on the axis of quantization is an example of spectroscopic stability. In his book, Van Vleck devoted considerable space to the “principle” or the “theorem” of spectroscopic stability (Van Vleck 1932b, 111, 139). Before giving a mathematical proof (ibid., sec. 35, 137–143), he explained the situation qualitatively in the chapter on the old quantum theory (ibid., sec. 30, 111–113). After conceding that the term, which he took from
[I]t can for our purposes be considered identical with the idea that the susceptibility is invariant of the type of quantization, or in the special case of spacial quantization, that summing over the various quantized orientations is equivalent, as far as results are concerned, to a classical integration over a random orientation of orbit. It is indeed remarkable that a discrete quantum summation gives exactly the same answers as a continuous integration. This was not at all true in the old quantum theory. (Van Vleck 1932b, 111)
In the three subsections that follow, we present derivations of the formula for the electric susceptibility in gases in classical theory (sec. 7.5.3), the old quantum theory (sec. 7.5.4), and quantum mechanics (sec. 7.5.5). In the quantum theory, old and new, we focus on the special case in which the gas molecules are modeled as rigid rotators. We will see how the robustness of the value
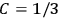 was established, lost, and regained. In secs. (7.5.3) and (7.5.5), we follow Van Vleck (1932b). In sec. (7.5.4), we follow
was established, lost, and regained. In secs. (7.5.3) and (7.5.5), we follow Van Vleck (1932b). In sec. (7.5.4), we follow
7.5.3 Susceptibilities in Classical Theory
The susceptibility of a gas,
 , is a measure of how the gas responds to external fields. We will consider the electric susceptibility in particular. The field,
, is a measure of how the gas responds to external fields. We will consider the electric susceptibility in particular. The field,
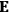 , and polarization,
, and polarization,
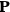 , are assumed to be parallel, and the medium is assumed to be both isotropic and homogenous. Predictions of
, are assumed to be parallel, and the medium is assumed to be both isotropic and homogenous. Predictions of
 require one to deal with the motions of the systems used as models for the gas molecules and their constituent atoms: the specific behavior of these systems in response to the external field will determine their electric moments, and in turn, the polarization of the medium.
require one to deal with the motions of the systems used as models for the gas molecules and their constituent atoms: the specific behavior of these systems in response to the external field will determine their electric moments, and in turn, the polarization of the medium.
Consider a small volume of a gas of molecules with permanent dipole moments, such as HCl. When an electric field is applied, say in the
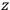 -direction of the coordinate system we are using, the molecules experience a torque that tends to align them with the field. In addition, the charges in each molecule will rearrange themselves in response. If the field is too weak to cause ionization, the charges will settle into equilibrium with the field, creating a temporary induced electric moment. Both of these effects contribute to a molecule’s electric moment
-direction of the coordinate system we are using, the molecules experience a torque that tends to align them with the field. In addition, the charges in each molecule will rearrange themselves in response. If the field is too weak to cause ionization, the charges will settle into equilibrium with the field, creating a temporary induced electric moment. Both of these effects contribute to a molecule’s electric moment
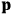 . Following Van Vleck, we largely focus on the first of these effects, which, as mentioned above, is responsible for the temperature-dependent term in the
. Following Van Vleck, we largely focus on the first of these effects, which, as mentioned above, is responsible for the temperature-dependent term in the
To find the polarization,
 , we need to take two averages over the component of these electric moments in the direction of the field
, we need to take two averages over the component of these electric moments in the direction of the field
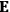 , in this case the
, in this case the
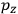 component. First, we need to average
component. First, we need to average
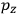 over the period(s) of the motion of the molecule (or in the case of quantum theory, over the stationary state). This is indicated by a single overbar:
over the period(s) of the motion of the molecule (or in the case of quantum theory, over the stationary state). This is indicated by a single overbar:
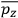 . Second, we need to average this time-average
. Second, we need to average this time-average
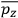 over a thermal ensemble of a large number
over a thermal ensemble of a large number
 of such molecules. This is indicated by a double overbar:
of such molecules. This is indicated by a double overbar:
 . All derivations of expressions for the susceptibility call for this two-step averaging procedure.58
. All derivations of expressions for the susceptibility call for this two-step averaging procedure.58
The strength
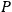 of the polarization is given by:
of the polarization is given by:
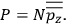
|
7.9 |
The electric susceptibility,
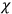 , is defined as the ratio of the strengths of the polarization and the external field:
, is defined as the ratio of the strengths of the polarization and the external field:
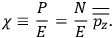
|
7.10 |
When it comes to the derivation of expressions for
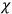 , the various theories differ only in how
, the various theories differ only in how
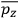 and
and
 are obtained.
are obtained.
We first go through the calculation in the classical theory, covered elegantly in chap. II of Van Vleck’s book, “Classical Theory of the Langevin-Debye Formula” (Van Vleck 1932b, 27–41). Consider a multiply-periodic system with
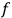 degrees of freedom, which, in its unperturbed state, is described by the Hamiltonian
degrees of freedom, which, in its unperturbed state, is described by the Hamiltonian
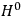 , and which is subjected to a small perturbation coming from an external electric field
, and which is subjected to a small perturbation coming from an external electric field
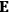 in the
in the
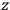 -direction. The Hamiltonian for the perturbed system can then be written as the sum
-direction. The Hamiltonian for the perturbed system can then be written as the sum
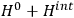 , where
, where
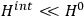 . In this case, the full Hamiltonian is given by:
. In this case, the full Hamiltonian is given by:
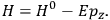
|
7.11 |
As in his NRC Bulletin, Van Vleck (1932b, 38) used action-angle variables
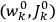
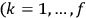 ) for the unperturbed Hamiltonian
) for the unperturbed Hamiltonian
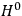 , even when dealing with the full Hamiltonian (see also Van Vleck 1927b, 50; cf. our discussion in sec. 7.3.2).
, even when dealing with the full Hamiltonian (see also Van Vleck 1927b, 50; cf. our discussion in sec. 7.3.2).
The
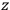 -component of the polarization of the system,
-component of the polarization of the system,
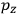 , can be written as a Fourier expansion. For a system with only one degree of freedom the expansion is given by:59
, can be written as a Fourier expansion. For a system with only one degree of freedom the expansion is given by:59
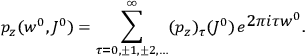
|
7.12 |
Essentially the same Fourier expansion is the starting point both for the derivation of the
To ensure that
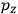 in eq. (7.12) is real, the complex amplitudes
in eq. (7.12) is real, the complex amplitudes
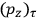 must satisfy
must satisfy
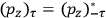 . Eq. (7.12) also gives the expansion for a system with
. Eq. (7.12) also gives the expansion for a system with
 degrees of freedom, if, following Van Vleck, we introduce the abbreviations
degrees of freedom, if, following Van Vleck, we introduce the abbreviations
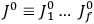 ,
,
 ,
,
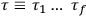 , and
, and
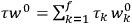 (Van Vleck 1932b, 38). Through
(Van Vleck 1932b, 38). Through
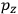 , the full Hamiltonian,
, the full Hamiltonian,
 , in eq. (7.11) depends on
, in eq. (7.11) depends on
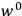 , so the action-angle variables
, so the action-angle variables
 are not action-angle variables for
are not action-angle variables for
 . The phase space element, however, is invariant under the transformation from action-angle variables for
. The phase space element, however, is invariant under the transformation from action-angle variables for
 to action-angle variables for
to action-angle variables for
 , i.e.,
, i.e.,
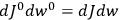 (ibid., 39).
(ibid., 39).
Using the standard formula for the canonical ensemble average, we find for
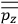 (ibid., 38):61
(ibid., 38):61

|
7.13 |
To first order in the field
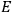 , the Boltzmann factor is given by:
, the Boltzmann factor is given by:
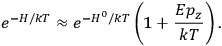
|
7.14 |
Assuming there is no residual polarization in the absence of an external field (which is true for gases if not always for solids), i.e.,
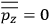 for
for
 , we have
, we have
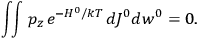
|
7.15 |

|
7.16 |
For
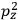 we insert its Fourier expansion
we insert its Fourier expansion
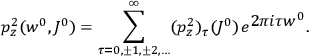
|
7.17 |
Only the
 terms on the right-hand side will contribute to the integral of
terms on the right-hand side will contribute to the integral of
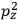 over
over
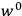 in eq. (7.16). All
in eq. (7.16). All
 terms are periodic functions of
terms are periodic functions of
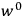 , which vanish when integrated over a full period of these functions. Hence,
, which vanish when integrated over a full period of these functions. Hence,

|
7.18 |
In other words,
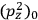 is the time average
is the time average
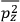 of
of
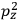 . It follows from eq. (7.18) that the integrals over
. It follows from eq. (7.18) that the integrals over
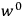 in numerator and denominator of eq. (7.16) cancel. Eq. (7.16) thus reduces to (ibid., 39–40):
in numerator and denominator of eq. (7.16) cancel. Eq. (7.16) thus reduces to (ibid., 39–40):
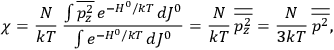
|
7.19 |
where in the last step we used that
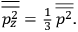
|
7.20 |
This relation holds both in the classical theory and in quantum mechanics. That it does not hold in the old quantum theory is central, as we will see, to that theory’s failure to reproduce the
denotes the statistical mean square of
in the absence of the field
, i.e. the average over only the
part of the phase space, weighted according to the Boltzmann factor, of the time average value of
[in our notation:
] for a molecule having given values of the
’s [recall that
short-hand for
]. Now if the applied electric field
is the only external field, all spacial orientations will be equally probable when
, and the mean squares of the
,
, and
components of moment will be equal [i.e.,
]. This will also be true even when there are other external fields (e.g. a magnetic field) besides the given electric field[,] provided, as is usually the case, these other fields do not greatly affect the spacial distribution. We may hence replace
by one-third the statistical mean square of the vector momentum
of the molecule. (Van Vleck 1932b, 39–40)
In the old quantum theory, as pointed out by
Van Vleck (1932b) called eq. (7.19) “a sort of generalized Langevin-Debye formula” (40). No particular atomic model need be assumed for its derivation. To obtain the familiar Langevin-Debye formula (7.7) with terms corresponding to permanent and induced electric moments, we need to adopt a model for the molecule of the gas similar to that underlying the classical dispersion theory of  be the number of degrees of freedom with which these bound charges can vibrate, then with a set of normal coordinates
be the number of degrees of freedom with which these bound charges can vibrate, then with a set of normal coordinates
 , we can write the component of the electric moment
, we can write the component of the electric moment
 along the principal axis of inertia, labeled
along the principal axis of inertia, labeled
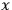 , as a linear function of these normal coordinates (ibid., 33):
, as a linear function of these normal coordinates (ibid., 33):
|
7.21 |
where
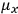 is the
is the
 -component of the permanent electric dipole moment of the molecule, and where the coefficients
-component of the permanent electric dipole moment of the molecule, and where the coefficients
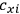 are real positive numbers. Similar expressions obtain for the
are real positive numbers. Similar expressions obtain for the
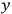 - and
- and
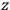 -components of
-components of
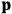 .
.
Since positive and negative displacements will cancel during the averaging process,
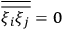 for
for
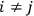 (ibid., 40). If we associate a ‘spring constant’
(ibid., 40). If we associate a ‘spring constant’
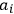 with the linear force binding the i-th charge, then, by the equipartition theorem, we get:
with the linear force binding the i-th charge, then, by the equipartition theorem, we get:
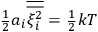 . Inserting eq. (7.21) for
. Inserting eq. (7.21) for
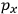 and similar equations for
and similar equations for
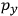 and
and
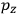 for the components of
for the components of
 in eq. (7.19) and using the relations for
in eq. (7.19) and using the relations for
 and
and
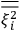 , we find (ibid., 37):
, we find (ibid., 37):
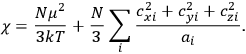
|
7.22 |
As desired, the first term gives us the contribution of the permanent moment with a factor of
 , and the second is of the form
, and the second is of the form
 , where
, where
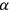 is independent of temperature.
is independent of temperature.
Unfortunately, the assumption that electrons can be thought of as harmonically-bound charges in the atom had to be discarded as the old quantum theory began to shed light on atomic structure. This is the same development that was responsible for the old quantum theory’s
A model such as we have used, in which the electronic motions are represented by harmonic oscillators, is not compatible with modern knowledge of atomic structure […] Inasmuch as we have deduced a generalizedLangevin-Debye formula for any multiply periodic system, the question naturally arises whether [eq. 7.19] cannot be specialized in a fashion appropriate to a real Rutherford atom instead of to a fictitious system of oscillators mounted on a rigid rotating framework. This, however, is not possible. (Van Vleck 1932b, 41)
The reason Van Vleck gave for this is that, in the Rutherford(-Bohr) atom, the energy of the electron ranges from
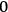 to
to
 causing the
causing the 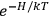 to diverge. Hence, he concluded, “the practical advantages of the [general formula 7.19] are somewhat restricted because of the inherent limitations in classical theory” (ibid.).
to diverge. Hence, he concluded, “the practical advantages of the [general formula 7.19] are somewhat restricted because of the inherent limitations in classical theory” (ibid.).
7.5.4 Susceptibilities in the Old Quantum Theory
Attempts to derive a formula for susceptibility in the old quantum theory, similar to the one in classical theory given above, ran afoul of some of the old quantum theory’s most striking yet little-known inconsistencies. The old quantum theory was at its best when physicists could be agnostic about the details of the multiply-periodic motion in atoms or molecules (as in the case of the
the old quantum theory replaced the factor[in the
Langevin-Debye formula 7.7] by a constant whose numerical value depended rather chaotically on the type of model employed, whether whole or half quanta were used, whether there was “weak” or “strong” spacial quantization, etc.63 This replacement of
by
caused an unreasonable discrepancy with the classical theory at high temperatures, and in some instances the constant
even had the wrong sign. (Van Vleck 1927a, 728)
The issue of ‘weak’ or ‘strong’ quantization mentioned in this passage has to do with the question of how to quantize the unperturbed motion in the old quantum theory. Consider a rotating molecule. If a strong enough electric field is present, it makes sense to quantize the molecule’s rotation with respect to the direction of the field. But how to quantize in the absence of an external field? In that case, there is no reason to assume a preferred direction in space, and it seems arbitrary to preclude entire classes of rotational states. Yet one had to proceed somehow. Two different kinds of quantization could be assumed (Van Vleck 1932b, 106). In the first, called ‘strong spatial quantization,’ rotation was assumed to be quantized with respect to the field even when there was, as yet, no field. In the other, called ‘weak spatial quantization,’ molecules were assumed to be in some intermediate state between ‘strong quantization’ and a classical distribution of rotational states.64 Van Vleck highlighted this conceptual conundrum:
Spacial quantization cannot be effective unless it has some axis of reference. In the calculation ofPauli and Pauling […] the direction of the electric field is taken as such an axis […] [I]n the absence of all external fields […] there is no reason for choosing one direction in space rather than another for the axis of spacial quantization. (Van Vleck 1932b, 108)
We need to take a closer look at these calculations by  and the azimuthal coordinate
and the azimuthal coordinate
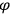 , and their conjugate angular momenta
, and their conjugate angular momenta
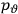 and
and
 . The angle
. The angle
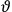 is measured from the
is measured from the
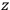 -axis chosen in the direction of the external field
-axis chosen in the direction of the external field
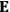 . The Hamiltonian for the system in this field is:
. The Hamiltonian for the system in this field is:
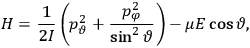
|
7.23 |
where
 is the molecule’s moment of inertia (Pauli 1921, 321).65
is the molecule’s moment of inertia (Pauli 1921, 321).65
Implicitly assuming strong spatial quantization,
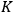 and
and
 , defined as (a sum of) action variables subject to
, defined as (a sum of) action variables subject to
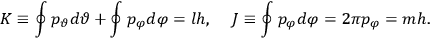
|
7.24 |
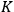 and
and
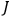 for these quantities and changed the first condition to66
for these quantities and changed the first condition to66
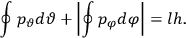
|
7.25 |
Both 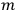 instead of
instead of
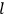 and
and
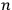 instead of
instead of
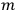 . We use
. We use
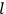 and
and
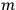 because it turns out that these quantum conditions boil down to setting the norm and the
because it turns out that these quantum conditions boil down to setting the norm and the
 -component of the angular momentum
-component of the angular momentum
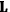 , both averaged over periods of
, both averaged over periods of
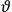 and
and
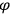 , equal to
, equal to
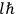 and
and
 , respectively (
, respectively (
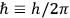 ). The reason Pauling modified Pauli’s first quantum condition was probably because he realized that
). The reason Pauling modified Pauli’s first quantum condition was probably because he realized that
 could never be smaller than
could never be smaller than
 . For the purposes of reconstructing the calculation (cf. note 68), the quantum conditions (7.24–7.25) can be replaced by:
. For the purposes of reconstructing the calculation (cf. note 68), the quantum conditions (7.24–7.25) can be replaced by:

|
7.26 |
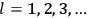 ;
;  . In both cases,
. In both cases,
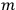 runs from
runs from
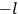 to
to
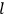 . The state
. The state
 was forbidden in the old quantum theory.
was forbidden in the old quantum theory.
The equations on the blackboard behind Van Vleck in the picture in fig. (3.1) may serve as a reminder that even this sanitized version (7.26) of the quantum conditions (7.24–7.25) is not how angular momentum is quantized in modern quantum mechanics.67 This modern treatment of angular momentum underlies the calculations of susceptibilities by
To find the susceptibility of a gas of rigid rotators in the old quantum theory, 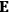 in a particular state of the rigid rotator characterized by the quantum numbers
in a particular state of the rigid rotator characterized by the quantum numbers
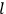 and
and
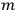 :
:

|
7.27 |
where
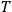 is the period of rotation. Substituting the classical equation
is the period of rotation. Substituting the classical equation
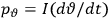 into the Hamiltonian in eq. (7.23) and using eq. (7.24) to set
into the Hamiltonian in eq. (7.23) and using eq. (7.24) to set
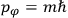 ,
,  to
to
 :
:

|
7.28 |
where
 , the value of
, the value of
 , is the total energy of the molecule (Pauli 1921, 322; Pauling 1926b, 570). Using eq. (7.28),
, is the total energy of the molecule (Pauli 1921, 322; Pauling 1926b, 570). Using eq. (7.28), 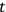 in eq. (7.27) by integration over
in eq. (7.27) by integration over
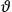 at the cost of a rather more complicated expression.
at the cost of a rather more complicated expression.
In the evaluation of
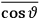 , a distinction needs to be made between two energy regimes (Pauli 1921, 322). In the first, the molecules have energies
, a distinction needs to be made between two energy regimes (Pauli 1921, 322). In the first, the molecules have energies
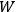 much smaller than
much smaller than
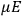 , the energy of the interaction between the electric moment and the field. In the second,
, the energy of the interaction between the electric moment and the field. In the second,
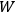 is much larger than
is much larger than
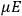 . The calculations of
. The calculations of  regime. In that case, we can take
regime. In that case, we can take
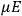 to be a small perturbation of a purely rotational Hamiltonian and expand the denominator on the right-hand side of eq. (7.28) in the small dimensionless parameter
to be a small perturbation of a purely rotational Hamiltonian and expand the denominator on the right-hand side of eq. (7.28) in the small dimensionless parameter
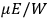 , keeping only first-order terms.
, keeping only first-order terms.
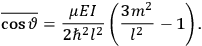
|
7.29 |
The ratio
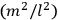 on the right-hand side corresponds to the time average
on the right-hand side corresponds to the time average
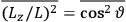 for the unperturbed system. In the classical theory,68
but not in the old quantum theory, the ensemble average,
for the unperturbed system. In the classical theory,68
but not in the old quantum theory, the ensemble average,
 , of this time average,
, of this time average,
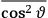 (both for the unperturbed system) is equal to
(both for the unperturbed system) is equal to
 .
This is the same point that Van Vleck (1932b, 39–40) made in one of the passages we quoted in sec. (7.5.3):
.
This is the same point that Van Vleck (1932b, 39–40) made in one of the passages we quoted in sec. (7.5.3):
 (see eq. 7.20). It thus follows from the classical counterpart of eq. (7.29) (see note 68) that the ensemble average,
(see eq. 7.20). It thus follows from the classical counterpart of eq. (7.29) (see note 68) that the ensemble average,
 , of the time average,
, of the time average,
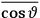 (now both for the perturbed system) vanishes.
(now both for the perturbed system) vanishes.
According to the classical theory, in other words, there is no contribution to the susceptibility at all from molecules in the energy regime
 for which the classical counterpart of eq. (7.29) (see note 68) was derived. As
for which the classical counterpart of eq. (7.29) (see note 68) was derived. As  is forbidden. In the old quantum theory, we thus have the paradoxical situation that there are “only such orbits present that according to the classical theory do not give a sizable contribution to the electrical polarization” (Pauli 1921, 325; emphasis in the original).
is forbidden. In the old quantum theory, we thus have the paradoxical situation that there are “only such orbits present that according to the classical theory do not give a sizable contribution to the electrical polarization” (Pauli 1921, 325; emphasis in the original).
 , of the time average,
, of the time average,
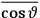 , given by eq. (7.29) does not vanish in the old quantum theory (where both averages are for the perturbed system). Hence, he concluded, in the old quantum theory the susceptibility does not come from molecules in the low energy states but from those in the high energy states of the
, given by eq. (7.29) does not vanish in the old quantum theory (where both averages are for the perturbed system). Hence, he concluded, in the old quantum theory the susceptibility does not come from molecules in the low energy states but from those in the high energy states of the
 regime in which eq. (7.29) holds. It therefore should not surprise us, Pauli argued, that the old quantum theory does not reproduce the factor
regime in which eq. (7.29) holds. It therefore should not surprise us, Pauli argued, that the old quantum theory does not reproduce the factor
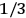 of the
of the
Before calculating
 ,
, 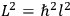 , tell us that the energy
, tell us that the energy
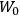 of the molecule in the absence of the field is given by:69
of the molecule in the absence of the field is given by:69
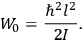
|
7.30 |
This energy, in turn, can be expressed in terms of a new quantity
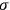 (Pauli 1921, 326):
(Pauli 1921, 326):
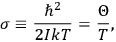
|
7.31 |
where
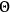 is a “temperature characteristic for the quantum drop in specific heat associated with the rotational degree of freedom” (ibid.). Combining eqs. (7.30) and (7.31), we see that
is a “temperature characteristic for the quantum drop in specific heat associated with the rotational degree of freedom” (ibid.). Combining eqs. (7.30) and (7.31), we see that
|
7.32 |

|
7.33 |
The ensemble average of
 is given by (Pauli 1921, 325):
is given by (Pauli 1921, 325):

|
7.34 |
where we used that, in the
 regime,
regime,
 can be replaced by
can be replaced by
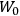 in the Boltzmann factors. Inserting eq. (7.33) for
in the Boltzmann factors. Inserting eq. (7.33) for
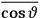 and using eq. (7.32) for
and using eq. (7.32) for
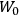 , we arrive at:
, we arrive at:
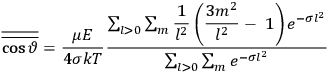
|
7.35 |
(Pauli 1921, 326; Pauling 1926b, 571). Evaluating these sums for integer and half-integer quantum numbers, respectively, and multiplying by
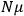 , both
, both 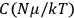 for the temperature-dependent term in the formula for electric susceptibilities. Using whole quanta, Pauli found
for the temperature-dependent term in the formula for electric susceptibilities. Using whole quanta, Pauli found
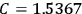 , which is 4.6 times the classical value of
, which is 4.6 times the classical value of
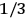 . Half-quanta—first introduced, at
. Half-quanta—first introduced, at 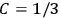 with half-quanta than Pauli had with whole quanta. For low temperatures (
with half-quanta than Pauli had with whole quanta. For low temperatures (
 ), Pauling calculated
), Pauling calculated
 to be
to be
 . In his theory, however,
. In his theory, however,
 increases with temperature and in the limit of
increases with temperature and in the limit of
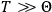 (a limit in which his calculation should have been entirely valid) takes on the value
(a limit in which his calculation should have been entirely valid) takes on the value
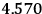 , over
, over
 times the classical value. As we saw in sec. (7.1.3), reliable experimental data to rule out values other than
times the classical value. As we saw in sec. (7.1.3), reliable experimental data to rule out values other than
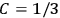 only became available after Pauling’s paper was published, but it certainly was odd that
only became available after Pauling’s paper was published, but it certainly was odd that
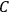 would increase with temperature in this way.
would increase with temperature in this way.
As we mentioned in sec. (7.4),
The new theory replaced eqs. (7.24–7.25) for the quantization of the rigid rotator’s angular momentum from the old quantum theory with relations familiar to the modern reader:71
|
7.36 |
where
 and
and
 (see, e.g., Mensing 1926, 814). Eq. (7.30) for the molecule’s rotational energy
(see, e.g., Mensing 1926, 814). Eq. (7.30) for the molecule’s rotational energy
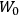 in the absence of a field accordingly changes to (Mensing and Pauli 1926, 510):72
in the absence of a field accordingly changes to (Mensing and Pauli 1926, 510):72
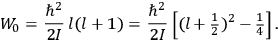
|
7.37 |
Hence, up to an additive constant, the energy is given by squares of half-integers rather than integers, as
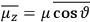 of the component of the dipole moment of the molecule in the direction of the field (cf. eq. 7.27). They wrote this in the form
of the component of the dipole moment of the molecule in the direction of the field (cf. eq. 7.27). They wrote this in the form
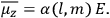
|
7.38 |
In the old quantum theory,
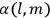 would be given by
would be given by
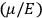 times the expression on the right-hand side of eq. (7.29) for
times the expression on the right-hand side of eq. (7.29) for
 . In the new quantum theory,
. In the new quantum theory,
 is given by
is given by
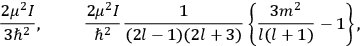
|
7.39 |
for
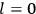 and
and
 , respectively (ibid., 512).73
, respectively (ibid., 512).73
These results can be used to calculate the ensemble average
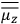 (cf. eqs. 7.34–7.35 for
(cf. eqs. 7.34–7.35 for
 in the old quantum theory). Setting
in the old quantum theory). Setting
 in the
in the
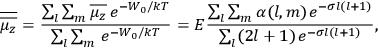
|
7.40 |
where, in the second step, we used the relation
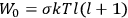 , the analogue in the new theory of the relation
, the analogue in the new theory of the relation
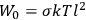 in the old one (see eq. 7.32), and evaluated the sum over
in the old one (see eq. 7.32), and evaluated the sum over
 in the denominator (ibid., 510).
in the denominator (ibid., 510).
When eq. (7.39) for
 is substituted into eq. (7.40) we find that only the
is substituted into eq. (7.40) we find that only the
 -term in the sum over
-term in the sum over
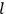 in the numerator contributes to
in the numerator contributes to
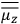 (ibid., 512).75 The contributions coming from
(ibid., 512).75 The contributions coming from
 can be written as:
can be written as:
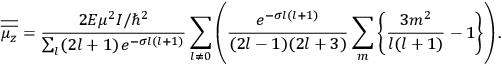
|
7.41 |
The well-known sum-of-squares formula tells us that
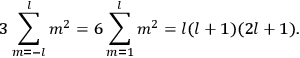
|
7.42 |
Using this formula to evaluate the sum over
 in eq. (7.41) for any fixed non-zero value of
in eq. (7.41) for any fixed non-zero value of
 , we find:76
, we find:76
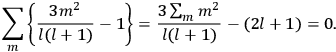
|
7.43 |
This shows that none of the
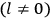 -terms in the sum over
-terms in the sum over
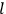 in the numerator of eq. (7.40) contribute to
in the numerator of eq. (7.40) contribute to
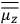 . As
. As 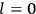 ] will therefore give a contribution to the temperature-dependent part of the dielectric constant” (512; emphasis in the original). The new quantum theory thus reverted to the classical theory in this respect.77
] will therefore give a contribution to the temperature-dependent part of the dielectric constant” (512; emphasis in the original). The new quantum theory thus reverted to the classical theory in this respect.77
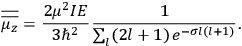
|
7.44 |
Using the relation
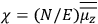 (see eq. 7.10) in combination with the expression
(see eq. 7.10) in combination with the expression
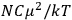 for the temperature-dependent term in
for the temperature-dependent term in
 (see eq. 7.8), we can write
(see eq. 7.8), we can write
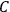 as:
as:

|
7.45 |
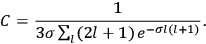
|
7.46 |
For sufficiently high temperatures,
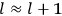 in most terms of the sum over the
in most terms of the sum over the
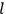 in the denominator, and the sum can be replaced by an integral:
in the denominator, and the sum can be replaced by an integral:
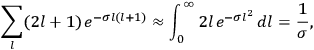
|
7.47 |
in which case
 .
.
This result is completely opposite to the results that were obtained on the basis of the earlier quantum theory of periodic systems according to which the coefficient[…] should have a numerical value substantially different from
even in the limiting case of high temperatures.78 This shows that here, as in many other cases, the new quantum mechanics follows classical mechanics more closely than the earlier quantum theory when it comes to statistical averages. (Mensing and Pauli 1926, 512)
And thus  , and thereby the vanishing of eq. (7.41), does not depend on the choice of the
, and thereby the vanishing of eq. (7.41), does not depend on the choice of the
 -axis for the quantization of
-axis for the quantization of
 . Van Vleck already indicated this in his brief note in Nature in 1926. Translated into our notation, he wrote:
. Van Vleck already indicated this in his brief note in Nature in 1926. Translated into our notation, he wrote:
The average value ofis then

|
which is obviously the same result as with random orientations.79 (Van Vleck 1926a, 227)
Note that this relation does not hold if the quantum-mechanical relation
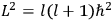 is replaced by the relation
is replaced by the relation
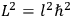 of the old quantum theory (see eq. 7.26). This is one way to understand the difficulties the old quantum theory ran into with susceptibilities. In quantum mechanics,
of the old quantum theory (see eq. 7.26). This is one way to understand the difficulties the old quantum theory ran into with susceptibilities. In quantum mechanics,
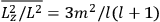 . In that case, the sum-of-squares formula tells us that the ensemble average
. In that case, the sum-of-squares formula tells us that the ensemble average
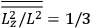 (see eqs. 7.39–7.43). In the old quantum theory,
(see eqs. 7.39–7.43). In the old quantum theory,
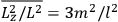 and
and
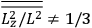 (see eqs. 7.33–7.35).
(see eqs. 7.33–7.35).
In subsequent publications, Van Vleck (1927a; 1932b) explained in more detail, and with greater generality, how the new quantum theory dispensed with the need for spatial quantization. This is precisely what is provided by the elusive notion of “spectroscopic stability” (cf. the quotations in sec. 7.5.2). Because of this general property of quantum mechanics, Van Vleck showed, it is true for a broad class of models and regardless of the axis along which one chooses to quantize that the only contribution to the susceptibility comes from the lowest energy states (the term
 in eq. (7.40) for the special case of the rigid rotator). This was true in classical theory as well, but not in the old quantum theory. As he explained in The Theory of Electric and Magnetic Susceptibilities:
in eq. (7.40) for the special case of the rigid rotator). This was true in classical theory as well, but not in the old quantum theory. As he explained in The Theory of Electric and Magnetic Susceptibilities:
[C]lassically the susceptibility arises entirely from molecules which possess so little energy that they would oscillate rather than rotate through complete circles […] As the temperature is increased, the fraction of molecules which are located in the ‘lazy’ states that contribute to the susceptibility will steadily diminish, and hence we can see qualitatively why the susceptibility due to permanent dipoles decreases with increasing temperature […] In the old quantum theory the susceptibility did not arise uniquely from the lowest rotational state […] and this is perhaps one reason why the old theory gave such nonsensical results on the dielectric constants.80 (Van Vleck 1932b, 184)
In blaming the “nonsensical results” of the old quantum theory on this unusual feature, Van Vleck ignored that, without it, the temperature-dependent term of the susceptibility could not be derived at all. In the case of the rigid rotator, the state
 was forbidden in the old quantum theory. The susceptibility thus had to come from the
was forbidden in the old quantum theory. The susceptibility thus had to come from the
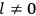 states. The preferred direction introduced by spatial quantization ensured that the sum over
states. The preferred direction introduced by spatial quantization ensured that the sum over
 in eqs. (7.34–7.35) for
in eqs. (7.34–7.35) for
 does not vanish, thus producing a non-zero contribution to the susceptibility. Without spatial quantization, all orientations would be equiprobable and the average moment in the direction of the field would be zero. We would then be stuck with the absurd conclusion that a permanent electric moment contributes nothing to the susceptibility! This is why, at the end of his paper,
does not vanish, thus producing a non-zero contribution to the susceptibility. Without spatial quantization, all orientations would be equiprobable and the average moment in the direction of the field would be zero. We would then be stuck with the absurd conclusion that a permanent electric moment contributes nothing to the susceptibility! This is why, at the end of his paper,
While spatial quantization thus offered make-shift solutions to some problems in the old quantum theory, it also introduced new ones. If one took it seriously, one was faced with a question about the quantization process itself. If it was somehow caused by the presence of a field, did it happen all at once or gradually as the field was applied? Either way, there would be physical consequences. Indeed, the experimentalist
If the reader has felt that our presentation of weak and strong quantization in the old quantum theory was somewhat mystifying (as indeed it had to be, as physicists themselves were hazy on the details of the passage from one type of quantization to another), he need now no longer feel alarmed, as the new mechanics gives no susceptibility effects without some analogue in classical theory. (Van Vleck 1932b, 111)
Spatial quantization also led to problems in the old quantum theory’s treatment of the effect of magnetic fields on the dielectric constant. It was
The investigation of the motion of a diatomic dipole molecule in crossed magnetic and electric fields shows that according to the old quantum theory there will be spatial quantization […] with respect to the magnetic field […] As a result of this the old quantum theory definitely requires that the application of a strong magnetic field to a gas such as hydrogen chloride produce a very large change in the dielectric constant of the gas. […] [T]he new quantum theory, on the other hand, requires the dielectric constant not to depend upon the direction characterizing the spatial quantization, so that no effect of a magnetic field would be predicted. The effect is found experimentally not to exist; so that it provides an instance of an apparently unescapable and yet definitely incorrect prediction of the old quantum theory. (Pauling 1927)
By late 1926, as this passage shows,
Van Vleck devoted a section of chap. V of his book to the issue raised by  found by
found by
The influence of a magnetic field on the dielectric constant […] was ludicrously large in the old quantum theory because of spacial quantization […] a crossed magnetic field would make the constantin [eq. 7.8] negative, an absurdity. Only a comparatively feeble magnetic field would be required […] An innocent little magnetic field of only a few gauss should thus in the old quantum theory change the sign of the temperature coefficient of the dielectric constant and make the electric susceptibility negative in so far as the orientation rather than induced polarization is concerned. This is what one might term extreme spectroscopic instability. Needless to say, such a cataclysmic influence of a magnetic field on the dielectric constant is not found experimentally […] In the new quantum mechanics the choice of the axis of spacial quantization is no longer of importance, and so a magnetic field should be almost without effect on the dielectric constant, in agreement with the experiments. (Van Vleck 1932b, 113–115)
In light of all this, it is no mystery that Van Vleck was so impressed by the way in which quantum mechanics dispensed with spatial quantization and, in the process, restored the factor of
 in the
in the  without the necessity of specifying the details of the model, and the generality of this value of
without the necessity of specifying the details of the model, and the generality of this value of
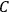 is one of the most satisfying features of the new theory” (Van Vleck 1932b, 107–108). This then is one of the “less heralded successes” and “great achievements” of the new quantum theory that Van Vleck was referring to in the preface of his book (see the quotation in sec. 7.1.1). The following subsection explores this achievement in greater detail.
is one of the most satisfying features of the new theory” (Van Vleck 1932b, 107–108). This then is one of the “less heralded successes” and “great achievements” of the new quantum theory that Van Vleck was referring to in the preface of his book (see the quotation in sec. 7.1.1). The following subsection explores this achievement in greater detail.
7.5.5 Susceptibilities in the New Quantum Mechanics
In this subsection, we present Van Vleck’s derivation, from his 1932 book, of the electric susceptibility of a diatomic gas, such as HCl, with the rigid rotator as the model for its molecules. The most important difference between this derivation and the one by
The 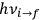 are either much greater or much smaller than
are either much greater or much smaller than
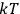 . Quantum mechanics thus solves the problem one runs into in the classical theory that the Langevin-Debye formula only obtains for unrealistic models of matter (see the quotation at the end of sec. 7.5.3). In other words, Van Vleck’s quantum-mechanical theory of susceptibilities can be seen as another instance of what
. Quantum mechanics thus solves the problem one runs into in the classical theory that the Langevin-Debye formula only obtains for unrealistic models of matter (see the quotation at the end of sec. 7.5.3). In other words, Van Vleck’s quantum-mechanical theory of susceptibilities can be seen as another instance of what
Van Vleck gave the general quantum-mechanical derivation of the
Following Van Vleck, we first derive an expression for the susceptibility of a gas without assuming a special model for its molecules. Let
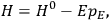
|
7.48 |
be the Hamiltonian for a gas molecule, represented by some multiply-periodic system, in an external electric field
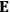 .
.
 is the Hamiltonian of the unperturbed system,
is the Hamiltonian of the unperturbed system,
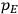 the electric moment of the system in the direction of the field. The quantities
the electric moment of the system in the direction of the field. The quantities
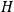 ,
,
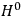 , and
, and
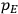 are now operators;
are now operators;
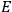 is still just a real number. The electric moment
is still just a real number. The electric moment
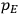 can be extracted from the Hamiltonian by taking the derivative with respect to the field strength:
can be extracted from the Hamiltonian by taking the derivative with respect to the field strength:
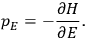
|
7.49 |
This relation is crucial for the calculation of the matrix elements of
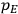 (143, 181).
(143, 181).
In general, Van Vleck wrote the Hamiltonian of a system subject to a small perturbation as
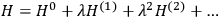 , with the parameter
, with the parameter
 (132). For the Hamiltonian in eq. (7.48),
(132). For the Hamiltonian in eq. (7.48),
 and
and
 is the only term in the expansion. Perturbation theory allowed Van Vleck to compute the energy of the perturbed system as a series of corrections to the energy of the unperturbed system, each term corresponding to a different power of the expansion parameter:
is the only term in the expansion. Perturbation theory allowed Van Vleck to compute the energy of the perturbed system as a series of corrections to the energy of the unperturbed system, each term corresponding to a different power of the expansion parameter:
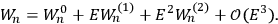
|
7.50 |
To second order, we have (133):
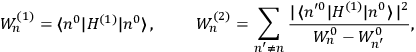
|
7.51 |
where the
 ’s are the eigenvectors of the unperturbed Hamiltonian.84 Combining eqs. (7.49) and (7.50), we obtain an expression for the matrix elements of the electric moment in eigenstates of the full Hamiltonian with eigenvectors
’s are the eigenvectors of the unperturbed Hamiltonian.84 Combining eqs. (7.49) and (7.50), we obtain an expression for the matrix elements of the electric moment in eigenstates of the full Hamiltonian with eigenvectors
 (ibid., 144):
(ibid., 144):
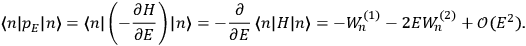
|
7.52 |
Inserting the expressions in eq. (7.51) for
 and
and
 , and using
, and using
 , we find, to first order in
, we find, to first order in
 (144):
(144):
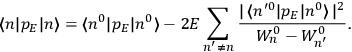
|
7.53 |
Van Vleck used the Bohr frequency condition to write
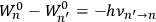 (133).85
(133).85
To find an expression for the susceptibility,
 , we need to take two averages (cf. the discussion leading up to eq. 7.9 in sec. 7.5.3): (1) the expectation value
, we need to take two averages (cf. the discussion leading up to eq. 7.9 in sec. 7.5.3): (1) the expectation value
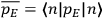 of the electric moment of an individual molecule in a given state; (2) the average
of the electric moment of an individual molecule in a given state; (2) the average
 of this expectation value over a thermal ensemble of
of this expectation value over a thermal ensemble of
 such molecules. Both steps are captured in the following formula (181; cf. eqs. 7.10, 7.13, and 7.19 in sec. 7.5.3):86
such molecules. Both steps are captured in the following formula (181; cf. eqs. 7.10, 7.13, and 7.19 in sec. 7.5.3):86
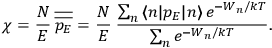
|
7.54 |
The 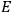 . Accordingly, we will assume the numerator in eq. (7.54) to be linear in
. Accordingly, we will assume the numerator in eq. (7.54) to be linear in
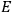 , and the denominator to be independent of
, and the denominator to be independent of
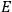 .
.

|
7.55 |
where in the last step we used eq. (7.51) for
 (with
(with
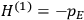 ). We now substitute eqs. (7.53) and (7.55) into eq. (7.54), keeping only terms to first order in the numerator and terms of zeroth order in the denominator. This gives us:
). We now substitute eqs. (7.53) and (7.55) into eq. (7.54), keeping only terms to first order in the numerator and terms of zeroth order in the denominator. This gives us:
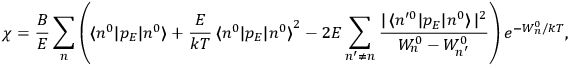
|
7.56 |
where
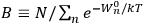 (190). The first term,
(190). The first term,
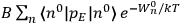 , represents the average electric moment in the absence of an external field. This kind of ‘hard’ polarization is nonexistent in gases, so the term must be zero (182). We are then left with (189):
, represents the average electric moment in the absence of an external field. This kind of ‘hard’ polarization is nonexistent in gases, so the term must be zero (182). We are then left with (189):
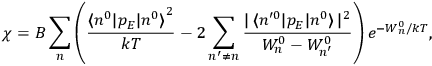
|
7.57 |
or equivalently, in terms of the energy corrections (182):
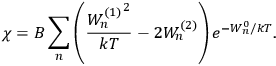
|
7.58 |
Eqs. (7.57–7.58) hold for any model of the constituent molecules of a gas. Van Vleck used it as a starting point for all of his electric susceptibility calculations, including the most general derivation of the
The Hamiltonian for a rigid rotator in an external electric field
 is given by (cf. eq. 7.23 in sec. 7.5.4):
is given by (cf. eq. 7.23 in sec. 7.5.4):
|
7.59 |
where
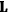 is the angular momentum and
is the angular momentum and
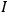 is the moment of inertia (cf. note 69). Consider the vectors
is the moment of inertia (cf. note 69). Consider the vectors
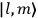 , which are simultaneous eigenvectors of
, which are simultaneous eigenvectors of
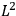 and
and
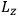 :
:
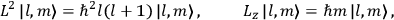
|
7.60 |
with
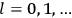 and
and
 . Since
. Since
 , these are also eigenvectors of the unperturbed Hamiltonian
, these are also eigenvectors of the unperturbed Hamiltonian
|
7.61 |
with (
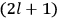 -fold degenerate) eigenvalues:
-fold degenerate) eigenvalues:

|
7.62 |
(cf. eq. 7.37 in sec. 7.5.4). The vector
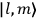 corresponds to the wave functions
corresponds to the wave functions
 (Baym 1969, 160) given by (sec. 37, 149):
(Baym 1969, 160) given by (sec. 37, 149):
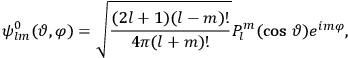
|
7.63 |
where the
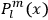 are associated Legendre functions.
are associated Legendre functions.
The susceptibility for a gas of rigid rotators is given by (182):
|
7.64 |
which is just the general eq. (7.58) for
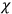 derived above with
derived above with
 and
and
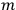 rather than
rather than
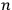 labeling the (degenerate) energy eigenstates. To find
labeling the (degenerate) energy eigenstates. To find
 , we need to find the first- and second-order energy corrections,
, we need to find the first- and second-order energy corrections,
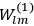 and
and
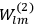 . Replacing subscripts
. Replacing subscripts
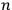 by
by
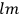 and vectors
and vectors
 by
by
 in eq. (7.51) and substituting
in eq. (7.51) and substituting
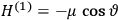 , we find (152):
, we find (152):
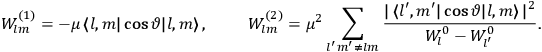
|
7.65 |
These expressions can be evaluated with the help of the following characteristic recursion formula for associated Legendre functions (151):
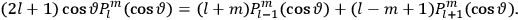
|
7.66 |
Combining this recursion formula with eq. (7.63), we find (ibid.)
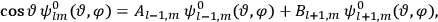
|
7.67 |
where we introduced the abbreviations:
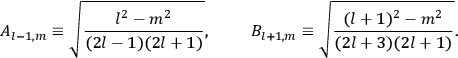
|
7.68 |
For
 , only the
, only the
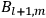 term is present. In terms of the corresponding state vectors, eq. (7.67) expresses that the vector obtained by letting the operator
term is present. In terms of the corresponding state vectors, eq. (7.67) expresses that the vector obtained by letting the operator
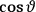 act on
act on
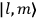 can be written as a linear combination of
can be written as a linear combination of
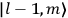 and
and
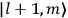 :88
:88
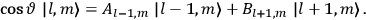
|
7.69 |
Since
 is orthogonal to
is orthogonal to
 as soon as
as soon as
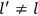 or
or
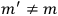 , it follows immediately from eq. (7.69) that
, it follows immediately from eq. (7.69) that
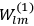 in eq. (7.65) vanishes, and that the only contributions to
in eq. (7.65) vanishes, and that the only contributions to
 come from terms with
come from terms with
 and
and
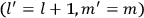 , for which we have:
, for which we have:

|
7.70 |
For
 , the expression for
, the expression for
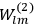 in eq. (7.65) thus reduces to:
in eq. (7.65) thus reduces to:
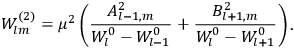
|
7.71 |
For
 , only the second term is present. Eq. (7.68) tells us that
, only the second term is present. Eq. (7.68) tells us that
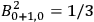 and eq. (7.62) that
and eq. (7.62) that
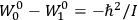 , which means that, for
, which means that, for
 , eq. (7.71) gives (152, 183):
, eq. (7.71) gives (152, 183):
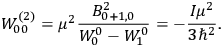
|
7.72 |
Using eq. (7.68) for
 and
and
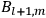 and eq. (7.62) for
and eq. (7.62) for
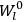 , Van Vleck showed that, for arbitrary non-zero values of
, Van Vleck showed that, for arbitrary non-zero values of
 and
and
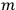 , eq. (7.71) becomes (ibid.):
, eq. (7.71) becomes (ibid.):
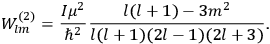
|
7.73 |
We now substitute these results for the energy corrections into eq. (7.64) for
 . Since
. Since
 , the equation reduces to:
, the equation reduces to:
|
7.74 |
Carrying out the sum over
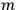 in the denominator, we can rewrite this as (183):
in the denominator, we can rewrite this as (183):
|
7.75 |
As we already saw in sec. (7.5.4), where we covered  term in the summation over
term in the summation over
 in the numerator gives a contribution to
in the numerator gives a contribution to
 . The terms for all other values of
. The terms for all other values of
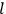 vanish. To verify this, we insert eq. (7.73) for
vanish. To verify this, we insert eq. (7.73) for
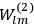 (
(
 ) in the sum over
) in the sum over
 in eq. (7.75):
in eq. (7.75):
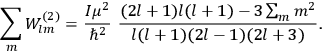
|
7.76 |
As Van Vleck noted (183), the numerator in this last expression vanishes on account of the formula
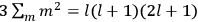 (152; cf. the sum-of-squares formula 7.42). The entire susceptibility thus comes from the
(152; cf. the sum-of-squares formula 7.42). The entire susceptibility thus comes from the
 term. This fits with the classical theory, for which
term. This fits with the classical theory, for which  .
.
Eq. (7.75) thus reduces to the
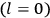 -term (184):
-term (184):
|
7.77 |
where, in the last step, we used eq. (7.72) for
 . Since
. Since
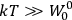 at the temperatures of interest, the
at the temperatures of interest, the 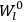 . At sufficiently high temperatures
. At sufficiently high temperatures
 for most terms in the sum, which can then be replaced by an integral (185; cf. eq. 7.47):
for most terms in the sum, which can then be replaced by an integral (185; cf. eq. 7.47):
|
7.78 |
With these approximations, eq. (7.77) becomes (185):
|
7.79 |
which is just the temperature-dependent term in the
Van Vleck did not bother to show explicitly that, despite appearances to the contrary, this derivation of the susceptibility of a gas of rigid rotators does not involve the choice of a preferred
 -axis for the quantization of
-axis for the quantization of
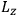 . For Van Vleck, this was just an instance of his general theorem of spectroscopic stability (137–143). To bring out the role of this theorem in this specific case, we prove that the susceptibility of a gas of rigid rotators is indeed independent of our choice of a
. For Van Vleck, this was just an instance of his general theorem of spectroscopic stability (137–143). To bring out the role of this theorem in this specific case, we prove that the susceptibility of a gas of rigid rotators is indeed independent of our choice of a
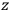 -axis. In the calculation above, we used the orthonormal basis
-axis. In the calculation above, we used the orthonormal basis
 to span the
to span the
 -dimensional subspace corresponding to the
-dimensional subspace corresponding to the
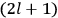 -fold degenerate energy eigenvalue
-fold degenerate energy eigenvalue
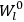 (see eq. 7.62). The number
(see eq. 7.62). The number
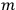 labels the different values of
labels the different values of
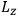 with respect to a
with respect to a
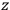 -axis chosen in the direction of the applied field
-axis chosen in the direction of the applied field
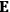 . We can span that same subspace with a different orthonormal basis
. We can span that same subspace with a different orthonormal basis
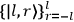 , where
, where
 labels the different values of
labels the different values of
 with respect to a
with respect to a
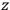 -axis in some arbitrary direction. The vectors in the old basis can be written in terms of the new one:
-axis in some arbitrary direction. The vectors in the old basis can be written in terms of the new one:
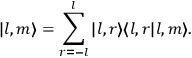
|
7.80 |
What we need to show is that the derivation of eq. (7.79) for the susceptibility of a gas of rigid rotators does not depend on whether we use
 or
or
 to label the degeneracy. More specifically, we need to check whether
to label the degeneracy. More specifically, we need to check whether
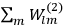 in eq. (7.75) is invariant under rotation of the
in eq. (7.75) is invariant under rotation of the
 -axis, i.e., under switching from the orthonormal basis
-axis, i.e., under switching from the orthonormal basis
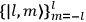 to the orthonormal basis
to the orthonormal basis
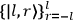 . Using eq. (7.65), we can write:
. Using eq. (7.65), we can write:
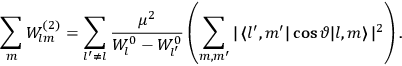
|
7.81 |
It is easy to show that
 and
and
 in the expression in parentheses can be replaced by
in the expression in parentheses can be replaced by
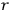 and
and
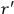 :90
:90
|
7.82 |
The derivation of the susceptibility, thus, does not depend on how the degeneracy in the energy levels
 is resolved.
is resolved.
To conclude our discussion of Van Vleck’s work in this area, we consider some features of his more general derivation of the  (eq. 7.20), i.e., the mean square average of the unperturbed electric moment in the
(eq. 7.20), i.e., the mean square average of the unperturbed electric moment in the
 -direction (the direction of the field even when the field is turned off) is
-direction (the direction of the field even when the field is turned off) is
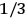 the mean square average of the total moment. In the classical theory, this is exactly what one would expect. When the field is turned off, there should be equal contributions to the mean square of the moment for each spatial dimension. This is exactly the feature, however, that was eliminated by spatial quantization in the old quantum theory. This made it possible for molecules in high-energy states to contribute to the temperature-dependent term in the Langevin-Debye formula (see our discussion in sec. 7.5.4).
the mean square average of the total moment. In the classical theory, this is exactly what one would expect. When the field is turned off, there should be equal contributions to the mean square of the moment for each spatial dimension. This is exactly the feature, however, that was eliminated by spatial quantization in the old quantum theory. This made it possible for molecules in high-energy states to contribute to the temperature-dependent term in the Langevin-Debye formula (see our discussion in sec. 7.5.4).
In the general quantum-mechanical derivation of the
|
7.83 |
As Van Vleck emphasized, and as we showed explicitly in the case of eq. (7.82) above, relations such as these are clearly, as Van Vleck put it somewhat awkwardly, “invariant of the choice of axis of quantization” (140). This relation is just one example of the more general theorem of spectroscopic stability that Van Vleck was able to prove in quantum mechanics (137–143). The upshot of this proof was that, in quantum mechanics, quantities like
 no longer depend on the axis of quantization as they had in the old quantum theory.
no longer depend on the axis of quantization as they had in the old quantum theory.
The strange story of the constant
 in the
in the 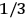 in both the classical and quantum-mechanical formulas express that mean squares of vector components do not depend on the axes with respect to which those averages are taken. In both theories,
in both the classical and quantum-mechanical formulas express that mean squares of vector components do not depend on the axes with respect to which those averages are taken. In both theories,
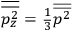 , where the
, where the
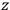 -direction can be arbitrarily chosen. The strange values of
-direction can be arbitrarily chosen. The strange values of
 in the old quantum theory resulted from the elimination of this very feature, which was essential if one wanted to derive the temperature-dependent term of the Langevin-Debye formula at all. Without spatial quantization there simply was no temperature-dependent term in the old quantum theory. Unfortunately, spatial quantization came with a whole raft of problems. In light of this, we can clearly see why Van Vleck used the story of
in the old quantum theory resulted from the elimination of this very feature, which was essential if one wanted to derive the temperature-dependent term of the Langevin-Debye formula at all. Without spatial quantization there simply was no temperature-dependent term in the old quantum theory. Unfortunately, spatial quantization came with a whole raft of problems. In light of this, we can clearly see why Van Vleck used the story of
 to illustrate the defects of the old quantum theory and the success of matrix mechanics in restoring the predictions of the classical theory.
to illustrate the defects of the old quantum theory and the success of matrix mechanics in restoring the predictions of the classical theory.
7.6 Kuhn Losses Revisited
Both Van Vleck’s 1926 Bulletin and his 1932 book do what
This is especially striking in the case of the 1932 book. Van Vleck spent roughly a third of his book (121 out of a total of 373 pages) on the classical theory (chaps. I–IV) and the old quantum theory (chap. V). One might argue that chap. V served a purely rhetorical purpose. The old quantum theory’s problems with susceptibilities are a great foil for the new quantum mechanics’ successes in that same area. Such use of history in a textbook can readily be reconciled with Kuhn’s views. There are two further considerations regarding this chapter that would seem to be in Kuhn’s favor. First, the history recounted in chap. V is somewhat misleading in that Van Vleck, inadvertently or deliberately, made it sound as if there had been reliable experimental evidence disproving the “wonderful nonsense” produced by the old quantum theory all along. In fact, such evidence had only become available around the time of the theory’s demise. Second, we know that Van Vleck wanted to cut chap. V to make room for new material when he began revising his book for a second edition decades later. He had no such plans, however, for chaps. I–IV on the classical theory.
The pedagogical goal of those early chapters was not merely to provide propaganda for the superior, quantum-mechanical treatment of susceptibilities. Rather, their main function was to prepare the reader for the quantum-mechanical calculation of susceptibilities by showing how such calculations are done in the classical theory. In his biographical memoir about his teacher,
Using older theories for pedagogical purposes in this way is not compatible with Kuhn’s picture. A new paradigm is supposed to come with its own new suite of tools for the pursuit of normal science. It is supposed to provide its own new set of exemplars to “show [students] by example how their job is to be done” (Kuhn 1996, 187; discussed in sec. ).
Van Vleck’s book provides a clear example of such an exemplar. It gives a general recipe with many concrete illustrations of how one can calculate susceptibilities, say the electric susceptibility of a gas. First, one has to decide on a mechanical system to model the constituent molecules of the gas. This can be a specific system (e.g., a rigid rotator) or a generic one (a classical multiply-periodic system solvable in action-angle variables, a quantum system with an energy spectrum satisfying some not overly restrictive conditions). One then has to do a perturbative calculation to compute the time-average of the component of the electric dipole moment in the direction of the external field of one copy of this system in a given state. Finally, one has to take the average of this time-average for an individual system over a thermal ensemble of many such systems in all possible states.
This general procedure works in classical theory, in the old quantum theory, and in modern quantum mechanics. The exemplar thus cuts across two paradigm shifts! Suman Seth (2010, 265–267) makes a similar point, when he contrasts a continuity of problems with a discontinuity in principles (see our discussion in sec. 7.1.5).
That the techniques from statistical mechanics for the calculation of ensemble averages work in all three theories does not seem to call for further comment. That this is also true for the perturbative techniques used to calculate the relevant time-averages is less obvious. These techniques were originally developed in the context of celestial mechanics. They were adapted to deal with atomic mechanics, to use
What lay behind, and made possible, this continuity of technique was a remarkable continuity of formalism in the transition from classical to quantum physics. Neither the old nor the new quantum theory did away with classical mechanics. The old quantum theory just added the
The “wonderful nonsense” produced on this score by 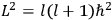 (
(
 ), sanctioned by modern quantum mechanics, they used
), sanctioned by modern quantum mechanics, they used
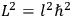 (Pauli with integer values, Pauling with half-integer values for
(Pauli with integer values, Pauling with half-integer values for
 , where
, where
 is forbidden in both cases). As a result, the ensemble average
is forbidden in both cases). As a result, the ensemble average
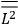 is not equal to three times the ensemble average
is not equal to three times the ensemble average
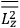 in the old quantum theory, whereas this relation does hold both in the classical theory and in quantum mechanics. Second, they saw themselves forced to adopt what Van Vleck (1927a, 37; 1932b, 110) later derided as the “bugbear” of spatial quantization.
in the old quantum theory, whereas this relation does hold both in the classical theory and in quantum mechanics. Second, they saw themselves forced to adopt what Van Vleck (1927a, 37; 1932b, 110) later derided as the “bugbear” of spatial quantization.
Matrix mechanics, the incarnation of quantum mechanics Van Vleck was most familiar and most comfortable with, retained the formalism of classical mechanics without inflicting this kind of disfigurement. This is remarkable because, unlike the old quantum theory, it radically changed the interpretation of the formalism. The basic idea of
Van Vleck saw these issues clearly only in retrospect. When he took the time to list and discuss the various flaws of the old quantum theory in his 1926 Bulletin, he did not include its failure to give a sensible result for electric susceptibilities. As we have seen, this was not because of ignorance (he had read the key paper by
Abbreviations and Archives
| AHQP | Archive for History of Quantum Physics. American Philosophical Society, Philadelphia |
| AIP-NBL | American Institute of Physics, Niels Bohr Library, College Park, MD |
Acknowledgments
We want to thank Massimiliano Badino, Rich Bellon, Tony Duncan, Fred Fellows, Clayton Gearhart, Don Howard, David Huber, Jeremiah James, Luc Janssen, Christian Joas, Marta Jordi, David Kaiser, Sally Gregory Kohlstedt, Christoph Lehner, Chun Lin, Joe Martin, Jaume Navarro, Jürgen Renn, Serge Rudaz, Rob “Ryno” Rynasiewicz, Roger Stuewer, and Arkady Vainshtein for helpful comments, discussion, and references. We are grateful to John Comstock for permission to use the pictures in figs. (3.1) and (7.3). Work on this paper was supported by Jürgen Renn’s department of the Max-Planck-Institut für Wissenschaftsgeschichte and by the National Science Foundation under grant STS–1027018.
References
Alexandrow, W. (1921). Eine Bemerkung zur Langevinschen Formel für die Suszeptibilität paramagnetischer Körper. Physikalische Zeitschrift 22: 258-259
Anderson, Philip W. (1987). John Hasbrouck Van Vleck, March 13, 1899–October 27, 1980. National Academy of Sciences Biographical Memoirs 56: 501-540
Baltas, Aristides, Kostas Gavroglu, K. G. (2000). A Discussion with Thomas S. Kuhn. In: The Road since Structure Ed. by James Conant, John Haugeland. Chicago: The University of Chicago Press 255-323
Baym, Gordon (1969). Lectures on Quantum Mechanics. Reading, MA: Addison-Wesley.
Bohr, Niels (1913). On the Constitution of Atoms and Molecules (Part I). Philosophical Magazine 6th Series 26: 1-25
- (1918). On the Quantum Theory of Line Spectra. Part II. On the Hydrogen Spectrum. Det Kongelige Danske Videnskabernes Selskab, Matematisk-fysiske Meddelser 4: 36-100
Bohr, Niels, Hendrik A. Kramers, H.A. K. (1924). The Quantum Theory of Radiation. Philosophical Magazine 6th Series 47: 785-802
Born, Max (1924). Über Quantenmechanik. Zeitschrift für Physik 26: 379-395
- (1925). Vorlesungen über Atommechanik. Berlin: Julius Springer.
- (1927). The Mechanics of the Atom. London: G. BellSons.
Born, Max, Werner Heisenberg, W. H. (1926). Zur Quantenmechanik II. Zeitschrift für Physik 35: 557-615
Born, Max, Pascual Jordan (1925). Zur Quantenmechanik. Zeitschrift für Physik 34: 858-888
- (1930). Elementare Quantenmechanik (Zweiter Band der Vorlesungen über Atommechanik). Berlin: Julius Springer.
Buchwald, Jed Z. (1985). From Maxwell to Microphysics: Aspects of Electromagnetic Theory in the Last Quarter of the Nineteenth Century. Chicago: The University of Chicago Press.
Cassidy, David C. (2007). Oppenheimer's First Paper: Molecular Band Spectra and a Professional Style. Historical Studies in the Physical and Biological Sciences 37: 247-269
Davisson, Clinton J. (1916). The Dispersion of Hydrogen and Helium on Bohr's Theory. Physical Review 8: 20-27
Debye, Peter (1912). Einige Resultate einer kinetischen Theorie der Isolatoren. Physikalische Zeitschrift 13: 97-100
- (1915). Die Konstitution des Wasserstoff-Moleküls. Sitzungsberichte der mathematisch-physikalischen Klasse der Königlichen Bayerischen Akademie der Wissenschaften zu München
Dennison, David M. (1926). The Rotation of Molecules. Physical Review 28: 318-333
Dirac, Paul A. M. (1925). The Fundamental Equations of Quantum Mechanics. Proceedings of the Royal Society A 109: 642-653
- (1930). The Principles of Quantum Mechanics. Oxford: Oxford University Press.
Duncan, Anthony, Michel Janssen (2007). On the Verge of . Archive for History of Exact Sciences 61: 553-624
- (2008). Pascual Jordan's Resolution of the Conundrum of the Wave-Particle Duality of Light. Studies in History and Philosophy of Modern Physics 21: 634-666
- (2013). (Never) Mind your p's and q's: Von Neumann versus Jordan on the Foundations of Quantum Theory. European Physical Journal H 38: 175-259
Einstein, Albert (1917). Zur Quantentheorie der Strahlung. Physikalische Zeitschrift 18: 121-128
Enz, Charles P. (2002). No Time to Be Brief. A Scientific Biography of Wolfgang Pauli. Oxford: Oxford University Press.
Epstein, Paul S. (1922). Die Störungsrechnung im Dienste der Quantentheorie. III. Kritische Bemerkungen zur Dispersionstheorie. Zeitschrift für Physik 9: 92-110
Fellows, Frederick H. (1985) J. H. Van Vleck: The Early Life and Work of a Mathematical Physicist. phdthesis. University of Minnesota
Feynman, Richard P., Robert B. Leighton, R.B. L. (1964). The Feynman Lectures on Physics. 3 Vols.. Reading, MA: Addison-Wesley.
Gearhart, Clayton A. (2010). “Astonishing Successes” and “Bitter Disappointment”: The Specific Heat of Hydrogen in Quantum Theory. Archive for History of Exact Sciences 64: 113-202
Gerlach, Walther, Otto Stern (1922). Das magnetische Moment des Silberatoms. Zeitschrift für Physik 9: 353-355
Heilbron, John L., Thomas S. Kuhn (1969). The Genesis of the Bohr Atom. Historical Studies in the Physical Sciences 1: 211-290
Heisenberg, Werner (1925a). Über eine Anwendung des Korrespondenzprinzips auf die Frage nach der Polarisation des Fluoreszenzlichtes. Zeitschrift für Physik 31: 617-626
- (1925b). Über die quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen. Zeitschrift für Physik 33: 879-893
Janssen, Michel, Matthew Mecklenburg (2007). From Classical to Relativistic Mechanics: Electromagnetic Models of the Electron. In: Interactions: Mathematics, Physics and Philosophy, 1860–1930 Ed. by Vincent F. Hendricks, Klaus F. Jørgensen, K.F. J., Lützen Klaus F.. Berlin: Springer 65-134
Jordan, Pascual (1936). Anschauliche Quantentheorie. Eine Einführung in die moderne Auffassung der Quantenerscheinungen. Berlin: Julius Springer.
Kemble, Edwin C. (1929). The General Principles of Quantum Mechanics. Part I. The Physical Review Supplement 1: 157-215
- (1937). The Fundamental Principles of Quantum Mechanics with Elementary Applications. New York: McGraw-Hill.
Kemble, Edwin C., Edward L. Hill (1930). The General Principles of Quantum Mechanics. Part II. Reviews of Modern Physics 2: 1-59
Kramers, Hendrik A. (1924a). The Law of Dispersion and Bohr's Theory of Spectra. Nature 113: 673-676
- (1924b). The Quantum Theory of Dispersion. Nature 114: 310-311
Kramers, Hendrik A., Werner Heisenberg (1925). Über die Streuung von Strahlung durch Atome. Zeitschrift für Physik 31: 681-707
Kronig, Ralph (1926a). The Dielectric Constant of Diatomic Dipole-Gases on the New Quantum Mechanics. Proceedings of the National Academy of Sciences 12: 488-493
- (1926b). The Dielectric Constant of Symmetrical Polyatomic Dipole-Gases on the New Quantum Mechanics. Proceedings of the National Academy of Sciences 12: 608-612
Kuhn, Thomas S. (1996). The Structure of Scientific Revolutions. Chicago: The University of Chicago Press.
Kuhn, Thomas S., John L. Heilbron, J.L. H., Forman John L. (1967). Sources for the History of Quantum Physics. An Inventory and Report. Philadelphia: American Philosophical Society.
Kuhn, Werner (1925). Über die Gesamtstärke der von einem Zustande ausgehenden Absorptionslinien. Zeitschrift für Physik 33: 408-412
Ladenburg, Rudolf (1921). Die quantentheoretische Deutung der Zahl der Dispersionselektronen.. Zeitschrift für Physik 4: 451-468
Ladenburg, Rudolf, Fritz Reiche (1923). Absorption, Zerstreuung und Dispersion in der Bohrschen Atomtheorie. Die Naturwissenschaften 11: 584-598
Langevin, Paul (1905a). Magnétisme et théorie des électrons. Annales de Chimie et de Physique 5: 70-127
- (1905b). Sur la théorie du magnétisme. Journal de Physique 4: 678-688
Lin, Chun C., Roger H. Stuewer, R.H. S. (1977). “On Minnesota" gave Wisconsin Its Popular Fight Song. Alumni News (University of Minnesota) December 1976/January 1977: 1
- (1980). Wisconsin versus Minnesota in Song. On Wisconsin 2:2 (Summer 1980): 4
Manneback, Charles (1926). Die Dielektrizitätskonstante der zweiatomigen Dipolgase nach der Wellenmechanik. Physikalische Zeitschrift 27: 563-569
Mehra, Jagdish, Helmut Rechenberg (1982a). The Historical Development of Quantum Theory. Vol. 3. The Formulation of Matrix Mechanics and Its Modifications, 1925–1926. New York: Springer.
- (1982b). The Historical Development of Quantum Mechanics. Vol. 4. Part 1: The Fundamental Equations of Quantum Mechanics, 1925–1926. Part 2: The Reception of the New Quantum Mechanics, 1925–1926. Berlin: Springer.
Mensing, Lucy (1926). Die Rotations-Schwingungsbanden nach der Quantenmechanik. Zeitschrift für Physik 36: 814-823
Mensing, Lucy, Wolfgang Pauli (1926). Über die Dielektrizitätskonstante von Dipolgasen nach der Quantenmechanik. Physikalische Zeitschrift 27: 509-512
Pauli, Wolfgang (1921). Zur Theorie der Dieelektrizitätskonstante zweiatomiger Dipolgase. Zeitschrift für Physik 6: 319-327
- (1930). Review of (Born and Jordan, 1930). Die Naturwissenschaften 18: 602
- (1933). Review of (Van Vleck, 1932b). Die Naturwissenschaften 21: 239
Pauling, Linus (1926a). The Quantum Theory of the Dielectric Constant of Hydrogen Chloride and Similar Gases. Proceedings of the National Academy of Sciences 12: 32-35
- (1926b). The Quantum Theory of the Dielectric Constant of Hydrogen Chloride and Similar Gases. Physical Review 27: 568-577
- (1927). The Influence of a Magnetic Field on the Dielectric Constant of a Diatomic Dipole Gas. Physical Review 29: 145-160
- (1932). Review of (Van Vleck, 1932b). The Journal of the American Chemical Society 54: 4119-4121
Pauling, Linus, Samuel Goudsmit (1930). The Structure of Line Spectra. New York: McGraw-Hill.
Rojansky, Vladimir (1938). Introductory Quantum Mechanics. Englewood Cliffs: Prentice-Hall.
Ruark, Arthur E. (1926). Review of (Van Vleck, 1926b). Journal of the Optical Society of America 13: 312
Ruark, Arthur E., Harold C. Urey (1930). Atoms, Molecules and Quanta. New York: McGraw-Hill.
Ruse, Michael (1989). The Darwinian Paradigm. Essays on Its History, Philosophy, and Religious Implications. LondonNew York: Routledge.
Schrödinger, Erwin (1926). Quantisierung als Eigenwertproblem. (Dritte Mitteilung). Störungstheorie, mit Anwendung auf den Starkeffekt der Balmerlinien. Annalen der Physik 80: 437-490
Serber, Robert (1992). The Los Alamos Primer. The First Lectures on How to Build an Atomic Bomb. Berkeley: University of California Press.
Seth, Suman (2010). Crafting the Quantum. Arnold Sommerfeld and the Practice of Theory, 1890–1926. Cambridge, MA: The MIT Press.
Smekal, Adolf (1927). Review of (Van Vleck, 1926b). Physikalische Zeitschrift 28: 62-63
Sommerfeld, Arnold (1915). Die allgemeine Dispersionsformel nach dem Bohrschen Modell. In: Festschrift Julius Elster und Hans Geitel Ed. by Karl Bergwitz. Braunschweig: Friedrich Vieweg und Sohn 549-584
- (1917). Die Drudesche Dispersionstheorie vom Standpunkte des Bohrschen Modelles und die Konstitution von H. Annalen der Physik 53: 497-550
- (1919). Atombau und Spektrallinien. Braunschweig: Friedrich Vieweg und Sohn.
- (1923). Atomic Structure and Spectral Lines. London: Methuen.
Stevens, K. W. H. (1995). Magnetism. In: Twentieth Century Physics. Vol. II Ed. by Laurie M. Brown, Abraham Pais, A. P.. BristolPhiladelphia/New York: Institute of Physics Publishing/American Institute of Physics Press 1111-1181
Stoner, Edmund C. (1932). Magnetism and Quantum Mechanics (Review of Van Vleck, 1932b). Nature 130: 490-491
Swann, William F. G., John T. Tate, J.T. T., Bateman John T. (1922). Electrodynamics of Moving Media. Washington: National Research Council (Bulletin of the National Research Council 4, Part 24).
Thomas, Willy (1925). Über die Zahl der Dispersionselektronen, die einem stationären Zustande zugeordnet sind (Vorläufige Mitteillung). Die Naturwissenschaften 13: 627
Van der Waerden, Bartel L. (1968). Sources of Quantum Mechanics. New York: Dover.
Van Vleck, John H. (1922). The Normal Helium Atom and Its Relation to the Quantum Theory. Philosophical Magazine 6th Series 44: 842-869
- (1924a). A Correspondence Principle for Absorption. Journal of the Optical Society of America 9: 27-30
- (1924b). The Absorption of Radiation by Multiply Periodic Orbits, and Its Relation to the Correspondence Principle and the Rayleigh-Jeans Law. Part I. Some Extensions of the Correspondence Principle. Physical Review 24: 330-346
- (1924c). The Absorption of Radiation by Multiply Periodic Orbits, and Its Relation to the Correspondence Principle and the Rayleigh-Jeans Law. Part II. Calculation of Absorption by Multiply Periodic Orbits. Physical Review 24: 347-365
- (1926a). Magnetic Susceptibilities and Dielectric Constants in the New Quantum Mechanics. Nature 118: 226-227
- (1926b). Quantum Principles and Line Spectra. Washington: National Research Council (Bulletin of the National Research Council 10, Part 4).
- (1927a). On Dielectric Constants and Magnetic Susceptibilities in the New Quantum Mechanics. Part I. A General Proof of the Langevin-Debye Formula. Physical Review 29: 727-744
- (1927b). On Dielectric Constants and Magnetic Susceptibilities in the New Quantum Mechanics. Part II. Application to Dielectric Constants. Physical Review 30: 31-54
- (1927c). The New Quantum Mechanics. Journal of the Optical Society of America 14: 108-112
- (1928a). On Dielectric Constants and Magnetic Susceptibilities in the New Quantum Mechanics. Part III. Application to Dia- and Paramagnetism. Physical Review 29: 587-613
- (1928b). The New Quantum Mechanics. Chemical Reviews 5: 467-507
- (1928c). The New Quantum Mechanics. Journal of the Optical Society of America 16: 301-306
- (1932a). Note sur les susceptibilités des ions Samarium et Europium. In: Le magnétisme. Rapport et discussions du sixième conseil de physique tenu à Bruxelles du 20 au 25 octobre 1930 Paris: Gauthier-Villars 55-64
- (1932b). The Theory of Electric and Magnetic Susceptibilities. Oxford: Oxford University Press.
- (1964). American Physics Comes of Age. Physics Today 17(6): 21-26
- (1968). My Swiss Visits of 1906, 1926, and 1930. Helvetica Physica Acta 41: 1234-1237
- (1971). Reminiscences of the First Decade of Quantum Mechanics. In: Symposium No. 5, 1971: A Symposium Held in Honor of Van Vleck Ed. by Per-Olov Lödwin. International Journal of Quantum Chemistry. New York: Wiley 3-20
- (1974). Acceptance Speech. Koninklijke Nederlandse Akademie van Wetenschappen. Bijzondere bijeenkomst der afdeling natuurkunde … 28 september 1974 … voor de plechtige uitreiking van de Lorentz-medaille aan Prof. Dr. J. H. Van Vleck.
- (1992a). John Hasbrouck Van Vleck (Autobiographical Note). In: Nobel Lectures in Physics (1971–1980) Ed. by Stig Lundqvist. Singapore: World Scientific Publishing 351-352
- (1992b). Quantum Mechanics: the Key to Understanding Magnetism. In: Nobel Lectures in Physics (1971–1980) Ed. by Stig Lundqvist. Singapore: World Scientific Publishing 353-369
Wigner, Eugene P. (1931). Gruppentheorie und ihre Anwendung auf die Quantenmechanik der Atomspektren. Berlin: Julius Springer.
Wigner, Eugene P., Andrew Szanton (1992). The Recollections of Eugene P. Wigner as Told to Andrew Szanton. New York: Plenum.
Zahn, Charles T. (1924). The Electric Moment of Gaseous Molecules of Halogen Hydrides. Physical Review 24: 400-417
Zahn, Charles T., A. H. Spees (1938). A Critical Analysis of the Classical Experiments on the Variation of Electron Mass. Physical Review 53: 511-521
Footnotes
AHQP interview, session 2, 5. See also the opening sentence of the preface of Van Vleck’s 1932 book quoted in sec. (7.1.1).
We thus use Kuhn’s work in the same spirit as Michael Ruse (1989, 62) in an essay on the plate-tectonics revolution in geology.
As we will see in sec. (7.4), there were four papers published in 1926 all reporting the recovery of
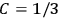 in the new quantum theory. As Van Vleck wrote in the conclusion of the one submitted first but published last: “This is a much more satisfactory result than in the older version of the quantum theory, in which both the calculations of Pauli [1921] with whole quanta […] and of Pauling [1926b] with half quanta yielded results diverging from the classical Langevin theory even at high temperatures” (Van Vleck 1926a, 227).
in the new quantum theory. As Van Vleck wrote in the conclusion of the one submitted first but published last: “This is a much more satisfactory result than in the older version of the quantum theory, in which both the calculations of Pauli [1921] with whole quanta […] and of Pauling [1926b] with half quanta yielded results diverging from the classical Langevin theory even at high temperatures” (Van Vleck 1926a, 227).
For a brief discussion of this phenomenon and its discovery in the nineteenth century, see (Buchwald 1985, 233, note 1).
Incidentally, Zahn, who concluded in 1924 that experiment could not decide between the classical formula for the temperature-dependence of electric susceptibilities and Pauli’s new quantum formula, is one of the two physicists who showed over a decade later that experiments on the velocity-dependence of the electron mass in the early years of the century could not decide between the theoretical predictions of Albert Einstein’s special theory of relativity and Lorentz’s ether theory, on the one hand, and Max Abraham’s so-called electromagnetic view of nature, on the other (Zahn and Spees 1938). As one of us has argued, the proponents of these competing theories, though paying lip service to the experimental results, especially when they favored their own theories, put much more stock in theoretical arguments (Janssen and Mecklenburg 2007, 105–108). When, for instance, Alfred H. Bucherer presented new data favoring Lorentz and Einstein at the same annual meeting of German Physical Scientists and Physicians in Cologne in 1908 where Hermann Minkowski gave his now famous talk on the geometrical underpinnings of special relativity, Minkowski, while welcoming Bucherer’s new data, dismissed Abraham’s theory on purely theoretical grounds. He called Abraham’s model of a rigid electron, not subject to length contraction, a “monster” and “no working hypothesis, but a working hindrance,” and compared Abraham’s insertion of this model into classical electrodynamics to attending a concert wearing ear plugs (ibid., 88)! This is reminiscent of how Van Vleck dismissed results derived by the likes of Pauli and Pauling in the old quantum theory as “wonderful nonsense.” As we will see in sec. (7.5.4), Van Vleck heaped more scorn on the treatment of susceptibilities in the old quantum theory in his 1932 book (Van Vleck 1932b, chap. V).
As we will see below, ‘paradigm’ is used here in the sense for which Kuhn (1996, 187) later introduced the term ‘exemplar’.
These notes, taken by Ralph P. Winch, have been deposited at the Niels Bohr Library & Archives of the American Institute of Physics in College Park, Maryland. Notes for a course in 1927–28 in Minnesota, taken by Robert B. Whitney and not nearly as meticulous as Winch’s, also contain numerous references to Van Vleck’s Bulletin. A full photocopy of these notes was obtained by Roger Stuewer, who kindly made them available to us (accompanying this photocopy is a letter from Barbara Buck to Roger Stuewer, 9 December 1977, detailing its provenance).
In his review of the 1932 book in Die Naturwissenschaften, Pauli (1933) wrote: “One can say that it has the character in part of a handbook and in part of a textbook. The former aspect is expressed in the exhaustive discussion of all questions of detail, the latter in that the foundations of the theory are also presented.” In summary, he wrote: “Both for learning the theory of the field covered and for an authoritative introduction to the details the book can be most warmly recommended” (ibid.). Similarly, Pauling (1932, 4121) wrote in his review: “The book is characterized by clear exposition and interesting style, which combined with the sound and reliable treatment, should make it a valuable text for an advanced course, as well as the authoritative reference book in the field.”
We are grateful to David Huber and Chun Lin at the University of Wisconsin–Madison, two of Van Vleck’s students, for providing us with copies of these revisions.
In the never completed manuscript of the revised edition, all of chap. V was “reduced to a single section of four typewritten pages” (Fellows 1985, 263).
Serber told Charles Weiner and Gloria B. Lubkin the same thing during an interview for the American Institute of Physics, 10 February 1967. As he put it in the interview, it was “always the same gang hanging on” (Fellows 1985, 294). As Van Vleck (1971, 17) noted with obvious relish about Serber: “One now identifies the present President of the American Physical Society with high energy physics, but before he fell under the influence of Oppenheimer at Berkeley, he worked on problems that today would be considered chemical physics.”
In 1936, Amelia Frank married Eugene Wigner, who had joined the faculty in Madison that year after having been dismissed by Princeton. She died only nine months later. Wigner thereupon accepted a new offer from Princeton, made at the recommendation of Van Vleck, who by this time was at Harvard (Wigner and Szanton 1992, 171–179).
Van Vleck Hall on the University of Wisconsin–Madison campus is named for E. B. Van Vleck.
In addition to three courses in physics, Van Vleck signed up for a course on railway operations in the Harvard Business School (AHQP interview, session 1, 3). As his wife Abigail recalled, Van Vleck abandoned the notion of pursuing a career in railroad management when the instructor asked him point blank whether he or anyone in his family actually owned a railroad (Fellows 1985, 16). Van Vleck, however, retained his fascination with railroads for the rest of his life. His knowledge of train schedules became legendary (Anderson 1987, 503). Years later, now on the faculty at Harvard, he told a colleague, the renowned historian of science I. Bernard Cohen, which trains to take on an upcoming trip. Although the information Van Vleck supplied, apparently off the top of his head, turned out to be perfectly accurate, Cohen was puzzled when he reached his destination and was told by his host that he could have left an hour later, yet arrived an hour earlier, had he taken a different combination of trains. Upon his return to Cambridge, Cohen confronted Van Vleck with this intelligence. Van Vleck was undaunted. “Of course,” he is reported to have said, “but wasn’t that the best beef lunch you ever had?” (We are grateful to Roger Stuewer for telling us this story, which he heard from I. B. Cohen.)
Sommerfeld sent a copy of the English translation of the third edition of his book to the University of Minnesota. This copy is still in the university’s library. He dedicated it to the graduate students of the University of Minnesota, which had been one of the earlier stops on his 1922–23 tour of American universities (see Michael Eckert’s contribution to this volume). The dedication is signed Munich, 16 October 19[23] (the last two digits, unfortunately, have been cut off). By the time this copy of Sommerfeld’s book arrived at the University of Minnesota, Van Vleck, as we will see, had joined its faculty.
As Gearhart (2010) concludes, “the story [of the specific heat of hydrogen] reminds us that the history of early quantum theory extends far beyond its better known applications in atomic physics” (193). This underscores the remark by Van Vleck with which we opened our paper about physicists in the early 1920s focusing strongly on spectroscopy. Although, as Gearhart shows, it drew much more attention in the old quantum theory than the problem of susceptibilities, the problem of specific heat is discussed only in passing by Van Vleck (1926b, 101–102) in his NRC Bulletin. There actually are some interesting connections between these two non-spectroscopic problems (see note 72).
AHQP interview, session 1, 14.
AHQP interview, session 1, 21.
AHQP interview, session 1, 21, emphasis in the original.
Foote to Van Vleck, 22 March 1924, AHQP.
Foote to Van Vleck, 22 March 1924, AHQP.
Van Vleck to Foote, 21 November 1924, AHQP.
Van Vleck to Foote, 10 August 1925, AHQP.
Van Vleck to Foote, 2 February 1926, AHQP.
Ruark approvingly referred to Van Vleck’s Bulletin a number of times in a book he wrote with Harold Urey a few years later (Ruark and Urey 1930).
The remaining chapters deal with “Half quanta and the anomalous Zeeman effect” (chap. XII) and “Light-quants” [sic] (chap. XIII).
For a detailed reconstruction of this derivation, which follows Van Vleck’s two-part paper of 1924 rather than his 1926 NRC Bulletin, see (Duncan and Janssen 2007): in sec. 3.4 (591–593), an outline of the derivation is given; in secs. 5.1–5.2 (627–637), the result is derived for a simple harmonic oscillator; in sec. 6.2 (648–652), this derivation is generalized to an arbitrary multiply-periodic system; finally, in sec. 7.1 (655–658), it is shown that in modern quantum mechanics the Kramers dispersion formula holds for an even broader class of systems than in the old quantum theory.
Ruark (1926) picked up on this distinction in his review of the Bulletin. Elaborating on his praise for the “refreshingly clear” treatment of the correspondence principle (see the quotation at the end of sec. 7.3.1), he explained that Van Vleck “takes pains to point out that certain asymptotic connections between quantum theory and classical dynamics can be definitely proved, while other connections are only postulated. Thus he distinguishes carefully the correspondence theorem for frequencies, and the correspondence postulates for intensities and polarization.” Cf. (Ruark and Urey 1930, chap. VI, sec. 2, “The correspondence theorem and the correspondence principles”).
The calculation of the effect of external fields on spectra, such as the Stark and Zeeman effects in atoms with one electron in external electric and magnetic fields, respectively, proceeds along similar lines (Van Vleck 1926b, chap. V).
This choice of variables is analogous to the one made in the Dirac interaction picture in time-dependent perturbation theory in modern quantum mechanics (Duncan and Janssen 2007, 655, note 204).
Born’s book is analyzed in Domenico Giulini’s contribution to this volume.
AHQP interview, session 1, 24, quoted by Duncan and Janssen (2007, 555–556).
The term ‘atomic mechanics’ (Atommechanik) was chosen in analogy with the term ‘celestial mechanics’ (Himmelsmechanik) (Born 1925, preface). For the English translation, the title was rendered as Mechanics of the Atom, but in the text “the clumsier expression atomic mechanics has often been employed” (Born 1927, v, note).
The next sentence is the one referring to Born’s discussions with Heisenberg and others quoted above.
AHQP interview, session 2, 2–3.
See also AHQP interview, session 2, 5.
Van Vleck wrote to Pauling in his capacity as associate editor to correct an error in the manuscript (Van Vleck to Pauling, April 27, 1926, AHQP; see note 76).
We will discuss these calculations by Pauli (1921) and Pauling (1926b) in detail in sec. (7.5.4) (see also Fellows 1985, 141–142).
Drawing the veil of charity over his subject’s 1921 paper on the topic, Pauli’s biographer Charles Enz (2002) concluded: “Thus Mensing and Pauli’s paper brought a long and confusing development to a close and helped establish faith in the new quantum theory” (63). Enz does not mention Van Vleck or Kronig. We will discuss the paper by Mensing and Pauli (1926) in sec. (7.5.4). This whole episode is also discussed briefly by Mehra and Rechenberg (1982b, 266–267).
AHQP interview, session 2, 5.
Referring to the 1926 note in his 1932 book, he described it as an “abstract only” (Van Vleck 1932b, 147). See (Fellows 1985, 143–148) for detailed discussion of Van Vleck’s note and a reconstruction of some of the derivations he suppressed for brevity.
In sec. (7.5.5), we will give the flavor of Van Vleck’s general derivation but we will only cover the details of his derivation for this special case.
Stuewer to Van Vleck, 11 October 1977 (telegram); Van Vleck to Stuewer, 16 November 1977. We are grateful to Roger Stuewer for providing us with copies of this correspondence.
The quotations are from Fowler to Van Vleck, 26 November 1928, and Van Vleck to Fowler, 28 November 1928 (Fellows 1985, 233–234).
For discussion of the book’s reception, see (Fellows 1985, 282–284).
As one of the reviewers of the book noted, “particular attention [is] being paid to the relation between the wave and matrix methods, a combination of which, in Van Vleck’s hands, has proved a powerful weapon in dealing with the problems under consideration” (Stoner 1932, 490).
Cf. the characterizations of Van Vleck’s book in the reviews by Pauli and Pauling quoted in note 8.
The electric susceptibility
 is related to the dielectric constant
is related to the dielectric constant
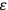 of the gas via:
of the gas via:
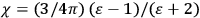 (see, e.g., Pauli 1921, 319; Pauling 1926b, 568; Van Vleck 1927b, 32; 1932b, 28).
(see, e.g., Pauli 1921, 319; Pauling 1926b, 568; Van Vleck 1927b, 32; 1932b, 28).
Yet another illustration of the continuity of Van Vleck’s research across the quantum revolution of 1925–26 is that the footnote inserted at this point refers to the subsection, “The Hypothesis of Spectroscopic Stability,” of sec. 54, “The Polarization of Resonance Radiation,” of his NRC Bulletin (Van Vleck 1926b, 171–173).
On the next page, before giving his general proof of spectroscopic stability, Van Vleck noted that a similar result for a special case had already been established in the Dreimännerarbeit (Born et.al. 1926, 590) and that he was “informed that the more general result has also been obtained independently by Born (unpublished)” (Van Vleck 1927a, 741). So, as in the old quantum theory (see sec. 7.3.2), Born and Van Vleck were pursuing similar lines of research in matrix mechanics. In the discussion of electric susceptibilities in their book, Born and Jordan (1930, sec. 42, 212–225) followed Van Vleck, citing (ibid., 219) his note in Nature and the trilogy in Physical Review (Van Vleck 1926a; 1927a; 1927b; 1928a). Born and Jordan did not use the term ‘spectroscopic stability’ in this context (see note 57).
This is how Van Vleck consistently spelled ‘spatial’.
Bohr introduced the term in the context of the Zeeman effect: “from a consideration of the necessary “stability” of spectral phenomena, it follows that the total radiation of the components, in which a spectral line, which originally is unpolarized, is split up in the presence of a small external field, cannot show characteristic polarisation with respect to any direction” (Bohr 1918, 85). Born and Jordan (1930, 13, 106, 161) attributed the term ‘spectroscopic stability’ to Heisenberg, citing a paper submitted in November 1924 on the polarization of fluorescent light (Heisenberg 1925a). Van Vleck also emphasized the connection between spectroscopic stability and the polarization of resonance radiation (Van Vleck 1926b, 171, see note 54; 1927a, 730; 1932b, 111). The first example Born and Jordan (1930, 12–13) gave of spectroscopic stability is the Thomas-Kuhn sum rule (see sec. 7.3.2). The “(optical) stability principle” is also mentioned prominently in a later book by Jordan (1936, 46–47, 169).
Pauling (1926b, 568) gives a particularly clear statement of this procedure: “[double bar] is the average value […] for all molecules in the gas, and [single bar] is the time average […] for one molecule in a given state of motion.”
Van Vleck (1932b, 38) writes
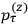 for the complex amplitudes
for the complex amplitudes
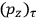 and suppresses the argument
and suppresses the argument
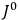 in his notation.
in his notation.
As Dennison put it in the introduction of the paper that Van Vleck (1926a) used for his note in Nature on the susceptibility of a gas of rigid rotators (see sec. 7.4): “According to [matrix mechanics] the coordinates of a multiply periodic system which may be expressed classically by means of multiple Fourier series in the time, are to be replaced by infinite matrices of the Hermite type of which each member is a harmonic component in time” (Dennison 1926, 318).
One can think of the integration of
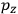 over one period of the angle variable
over one period of the angle variable
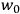 for a fixed value of
for a fixed value of
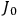 as giving
as giving
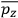 and of the subsequent integration over
and of the subsequent integration over
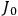 as turning
as turning
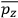 into
into
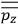 (ibid., note 11). In this case, averaging over a thermal ensemble of identical systems is replaced by taking a weighted average over different states of one system, where the weight factor is given by the usual Boltzmann factor
(ibid., note 11). In this case, averaging over a thermal ensemble of identical systems is replaced by taking a weighted average over different states of one system, where the weight factor is given by the usual Boltzmann factor
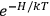 , in which
, in which
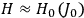 .
.
The same can be said about classical dispersion theory (Duncan and Janssen 2007, 576–577).
In Part II of his 1927–28 trilogy, Van Vleck (1927b, 37) referred to his NRC Bulletin for a discussion of ‘weak’ versus ‘strong’ quantization (Van Vleck 1926b, 165). In the Bulletin the same distinction is also made in terms of ‘diffuse’ versus ‘sharp’ quantization (ibid., 171–178).
Pauli used A and F and Pauling used I and F for what in our notation are I and E, respectively.
In a preliminary report on his results, Pauling (1926a, 33) did not take the absolute value of
 in this quantum condition.
in this quantum condition.
For a concise modern discussion of angular momentum in quantum mechanics, see, e.g., (Baym 1969, chap. 6).
Pauli (1921, sec. 4, 322–324), in fact, first showed that, in classical theory,
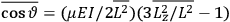 (in our notation, where the overbars on the left- and the right-hand sides refer to time averages for the perturbed and the unperturbed system, respectively). He then set
(in our notation, where the overbars on the left- and the right-hand sides refer to time averages for the perturbed and the unperturbed system, respectively). He then set
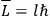 and
and
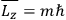 (cf. eq. 7.26) to turn this classical equation into eq. (7.29) in the old quantum theory.
(cf. eq. 7.26) to turn this classical equation into eq. (7.29) in the old quantum theory.
Using that
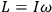 (with
(with
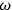 the angular frequency), we can rewrite the rotational energy
the angular frequency), we can rewrite the rotational energy
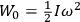 as
as
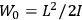 .
.
See (Cassidy 2007) for discussion of this paper.
We will continue to use the letter
 even though Mensing (1926), Mensing and Pauli (1926) and Van Vleck (1932b, sec. 37, 147–152; see sec. ) all used
even though Mensing (1926), Mensing and Pauli (1926) and Van Vleck (1932b, sec. 37, 147–152; see sec. ) all used
 instead. To a modern reader, the letter
instead. To a modern reader, the letter
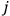 may suggest a combination of orbital angular momentum and spin, whereas in the case of the rigid rotator we only have the former,
may suggest a combination of orbital angular momentum and spin, whereas in the case of the rigid rotator we only have the former,
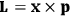 .
.
Note that, for
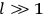 , the second expression in eq. (7.39) reduces to
, the second expression in eq. (7.39) reduces to
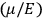 times on the right-hand side of eq. (7.29), the corresponding expression in the old quantum theory. In sec. (7.5.5), we will cover the corresponding step in Van Vleck’s (1932b, 151–152) calculation for the rigid rotator in more detail.
times on the right-hand side of eq. (7.29), the corresponding expression in the old quantum theory. In sec. (7.5.5), we will cover the corresponding step in Van Vleck’s (1932b, 151–152) calculation for the rigid rotator in more detail.
As we will see in sec. (7.5.5), Van Vleck (1932b, 182) was more careful with these Boltzmann factors.
Whereas the sum in eq. (7.41) for the new quantum theory vanishes, the corresponding sum in eq. (7.35) for the old quantum theory (in which
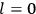 is forbidden) does not. It is because of this key difference between the calculation based on the modern quantum conditions (7.36) and the calculation based on the old quantum conditions (7.26) that the switch from whole to half quanta did nothing to bring the value for the electric susceptibility closer to what we now know to be the empirically correct one.
is forbidden) does not. It is because of this key difference between the calculation based on the modern quantum conditions (7.36) and the calculation based on the old quantum conditions (7.26) that the switch from whole to half quanta did nothing to bring the value for the electric susceptibility closer to what we now know to be the empirically correct one.
The error in the paper by Pauling (1926b) pointed out by Van Vleck (see note 40) occurred in a summation just like the one in eq. (7.43). Pauling considered the sum
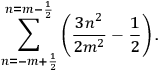
In the letter cited in note 40, Van Vleck commented: “I think the error resulted from counting the term
 only once instead of
only once instead of
 times in the summation.”
times in the summation.”
In his note on susceptibilities in Nature, Van Vleck (1926a, 227) made the same point: “The remarkable result is obtained that only molecules in the state [
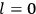 ] of lowest rotational energy make a contribution to the polarisation. This corresponds very beautifully to the fact that in the classical theory only molecules with energy less than [
] of lowest rotational energy make a contribution to the polarisation. This corresponds very beautifully to the fact that in the classical theory only molecules with energy less than [
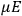 ] contribute to the polarisation.” Like Pauli (1921, 324), Van Vleck (1926a) cited Alexandrow (1921) for this result in the classical theory. So did Kronig (1926a, 491), who also drew attention to this analogy between classical theory and quantum mechanics.
] contribute to the polarisation.” Like Pauli (1921, 324), Van Vleck (1926a) cited Alexandrow (1921) for this result in the classical theory. So did Kronig (1926a, 491), who also drew attention to this analogy between classical theory and quantum mechanics.
Feynman, Leighton, and Sands (1964, Vol. 2, chap. 34, 11) used this same relation as an argument for why one should set
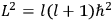 , if one sets
, if one sets
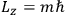 with
with
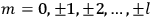 . It is only natural to demand that the average value of
. It is only natural to demand that the average value of
 be three times the average value of
be three times the average value of
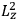 . The average value of
. The average value of
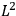 is then given by
is then given by
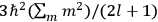 , which the sum-of-squares formula tells us is equal to
, which the sum-of-squares formula tells us is equal to
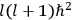 .
.
That the only contribution to the susceptibility comes from the lowest state is a special feature of the rigid rotator. It is true much more generally, however, that the bulk of the susceptibility comes from the lower energy states (ibid.).
In his interview for the AHQP, Pauling said: “I had already been especially struck by the fact that the Debye equation for the dielectric constant and the Langevin equation for paramagnetism are valid in quantum mechanics and that
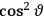 averages one third in quantum mechanics for all states if one interprets the total angular momentum vector as a square root of j times j plus one. I emphasized this strongly in the book.” (session 2, 12) The last sentence refers to a lengthy footnote in a book by Pauling and Samuel Goudsmit (1930, 231–232).
averages one third in quantum mechanics for all states if one interprets the total angular momentum vector as a square root of j times j plus one. I emphasized this strongly in the book.” (session 2, 12) The last sentence refers to a lengthy footnote in a book by Pauling and Samuel Goudsmit (1930, 231–232).
A footnote appended to the title of sec. 34, “Perturbation Theory,” acknowledges that perturbation theory in quantum mechanics was first developed in the Dreimännerarbeit (Born et.al. 1926) and in the third communication on wave mechanics by Erwin Schrödinger (1926).
We use modern Dirac notation both because it is more familiar to the modern reader and because it is the notation Van Vleck adopted when he began revising his 1932 book for a second edition (cf. sec. 7.1.5). In the 1932 book, he wrote what in our notation would be
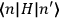 as
as
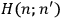 . He also typically used two or three quantum numbers to label the (degenerate) energy eigenstates, writing, for instance,
. He also typically used two or three quantum numbers to label the (degenerate) energy eigenstates, writing, for instance,
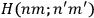 or
or
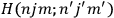 . We will follow his example in the case of the rigid rotator (see eq. 7.65).
. We will follow his example in the case of the rigid rotator (see eq. 7.65).
When he first published this formula, Van Vleck commented: “This is, of course, the same result as given by extrapolation of the Kramers dispersion formula to infinitely long impressed wavelengths” (Van Vleck 1927a, 734). Mensing and Pauli (1926, 511) and Kronig (1926a, 490) had made that same connection. In chap. XIII of his book, Van Vleck gave a formula for the index of refraction
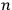 of some transparent material as an ensemble average of the polarization of its constituents, given by the Kramers dispersion formula (361):
of some transparent material as an ensemble average of the polarization of its constituents, given by the Kramers dispersion formula (361):
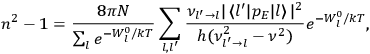
where
 is the frequency of the incident light wave and
is the frequency of the incident light wave and
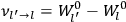 (cf. Duncan and Janssen 2007, 658). For
(cf. Duncan and Janssen 2007, 658). For
 , the sums over
, the sums over
 for fixed
for fixed
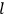 have the same form (modulo the Boltzmann factor) as the second term on the right-hand side of eq. (7.53). This underscores the relation between dispersion and susceptibility that we drew attention to in sec. (7.1.5) and at the beginning of sec. (7.5.2).
have the same form (modulo the Boltzmann factor) as the second term on the right-hand side of eq. (7.53). This underscores the relation between dispersion and susceptibility that we drew attention to in sec. (7.1.5) and at the beginning of sec. (7.5.2).
Even though in the modern view, the expectation value cannot be viewed as a time average, in 1932 Van Vleck considered it to be something very similar: “A diagonal Heisenberg matrix element
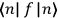 has the physical significance of being the average value of
has the physical significance of being the average value of
 over all the phases of motion in a given stationary state” (Van Vleck 1932b, 129).
over all the phases of motion in a given stationary state” (Van Vleck 1932b, 129).
Taking the inner product with an arbitary vector
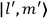 on both sides of eq. (7.69), we find:
on both sides of eq. (7.69), we find:
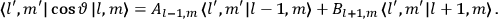
In coordinate space, these inner products turn into integrals:
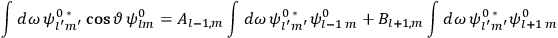
where
 and where we suppressed the argument
and where we suppressed the argument
 of the various
of the various
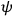 functions. Since
functions. Since
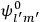 is arbitrary, this last relation implies eq. (7.67), the form in which Van Vleck gave eq. (7.69).
is arbitrary, this last relation implies eq. (7.67), the form in which Van Vleck gave eq. (7.69).
As Born and Jordan (1930, 222–223) noted in their textbook, this “was one of the first “practical” successes of the new quantum mechanics. The methods of the old quantum theory [here a footnote is inserted citing Pauli (1921)], in which a “directional quantization” of the axes of the molecules had to be imposed, lead to a wrong numerical factor at high temperatures.”
Instead of the angular momentum
 , Van Vleck considered a general vector quantity
, Van Vleck considered a general vector quantity
 .
.

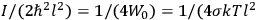 ). Using this relation, we can rewrite eq. (
). Using this relation, we can rewrite eq. (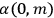 into eq. (
into eq. (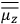 and using that
and using that
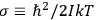 (see eq.
(see eq.  and
and
 in eq. (
in eq. ( and
and
 can be written as:
can be written as: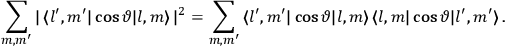
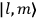 in terms of the vectors
in terms of the vectors
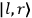 :
:
 run from
run from
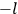 to
to
 and
and
 run from
run from
 to
to
 . Reordering the various factors, we find
. Reordering the various factors, we find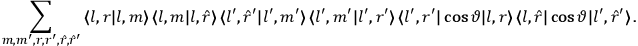
 and
and
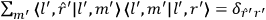 , this reduces to
, this reduces to