What we now know about Old Babylonian algebra—its flexibility, its operational power in the solution
The Scribe School
Old Babylonian mathematics was not the high-status diversion of wealthy and highly intelligent amateurs, as Greek mathematicians were or aspired to be. According to the format of its texts it was taught in the scribe
The word “scribe” might mislead. The scribe certainly knew to write. But the ability to calculate was just as important—originally, writing had been invented as subservient to accounting, and this subordinated function with respect to calculation remained very important. The modern colleagues of the scribe are engineers, accountants and notaries.
Therefore, it is preferable not to speak naively of “Babylonian mathematicians.” Strictly speaking, what was taught number- and quantity-wise in the scribe school should not be understood primarily as “mathematics” but rather as calculation. The scribe should be able to find the correct number, be it in his engineering function, be it as an accountant. Even problems that do not consider true practice always concern measurable magnitudes
That is one of the reasons that many of the problems
If we really want to find Old Babylonian “mathematicians” and
and
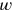 of a rectangle from its area and from the area of another rectangle
of a rectangle from its area and from the area of another rectangle
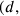

 (that is, a rectangle whose length is the diagonal of the first rectangle and whose width is the cube constructed on its length). This is a problem of the eighth degree
(that is, a rectangle whose length is the diagonal of the first rectangle and whose width is the cube constructed on its length). This is a problem of the eighth degree
The First Purpose: Training Numerical Calculation
When following the progression of one of the algebraic texts—in particular one of the more complicated specimens—one is tempted to trust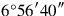 is
is
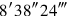 , and if that was not the case, the modern edition of the text would certain have inserted a footnote” (certain writing errors have indeed been corrected above, so all calculations should be correct). The reader who has been more suspicious will, on the other hand, have received a good training in sexagesimal arithmetic.
, and if that was not the case, the modern edition of the text would certain have inserted a footnote” (certain writing errors have indeed been corrected above, so all calculations should be correct). The reader who has been more suspicious will, on the other hand, have received a good training in sexagesimal arithmetic.
That illustrates one of the functions of algebra in the curriculum: it provided a pretext for training the manipulation of difficult numbers. As the aim of the school was the training of professional routine, the intensive cultivation of sexagesimal arithmetic was obviously welcome.
This observation can be transferred to our own epoch and its teaching of second-degree equations. Its aim was never to assist the copying of gramophone records or CDs to a cassette tape. But the reduction of complicated equations and the ensuing solution of second-degree equations is not the worst pretext for familiarizing students with the manipulation of symbolic algebraic expressions and the insertion of numerical values in a formula; it seems to have been difficult to find alternatives of more convincing direct practical relevance—and the general understanding and flexible manipulation of algebraic formulas and the insertion of numerical values in formulas are routines which are necessary in many jobs.
The Second Purpose: Professional Pride
The acquisition of professional dexterity is certainly a valid aim, even if it is reached by indirect means. Yet that was not the only purpose of the teaching of apparently useless mathematics. Cultural
Quite a few such texts are known. They speak little of everyday routines—the ability to handle these was too elementary, in order to be justified the pride of a scribe
To find the area of a rectangular field from its length and width was also not suited to induce much self-respect—any bungler in the trade could do that. Even the determination of the area of a trapezium was too easy. But to find a length and a width from their sum and the area they would “hold” was already more substantial; to find them from data such as those of AO 8862 #2,
We have no information about Sumerian and mathematics being used for social screening of apprentice-scribes—one of the functions of such matters in the school of today: Since the scribe school
Even analysis of the cultural function of “advanced” Old Babylonian mathematics may thus teach us something about our own epoch.
Footnotes
In the nineteenth century, precisely these three groups provided the bulk of subscribers to the Journal des mathématiques élémentaires and similar periodicals. The Ladies’ Diary, published from 1704 until 1841 and rich in mathematical contents, could also aim at a social group that was largely excluded from Oxford-Cambridge and public-school Latinity and Grecity, to which even genteel women had no access.
